Per calcolare il determinante di una matrice c'è un metodo poco noto detto metodo di Chiò, dal nome del matematico Felice Chiò. Si riporta brevemente questo metodo, la sua giustificazione e un foglio Excel con le relative formule.
Il determinante di una matrice
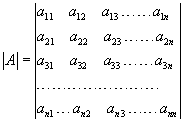
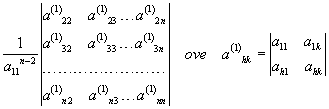
sono tutti i minori orlati del 2° ordine di a11(a11≠0 e h, k≥2).
Dimostrazione
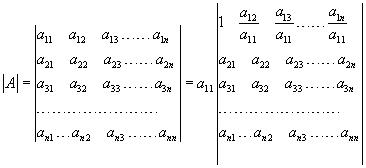
si è divisa la 1° riga per a11
si sostituisce alla 2° riga la seguente combinazione lineare: somma della 2° riga con la 1° moltiplicata per -a21;
si sostituisce alla 3° riga la seguente combinazione lineare: somma della 3° riga con la 1° moltiplicata per –a31;
...................................................................................................................................................................
si sostituisce alla n° riga la seguente combinazione lineare: somma della n° riga con la 1° moltiplicata per –an1.
Si ottiene:
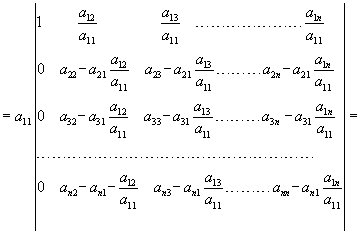
Si moltiplicano tutte le righe, tranne la 1°, per a11 e si ottiene:
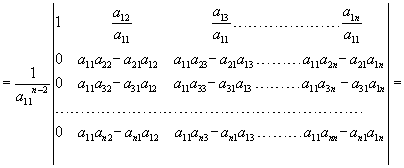
Applicando Laplace si ha la tesi:
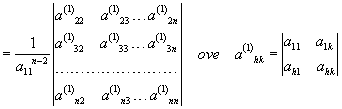
sono tutti i minori orlati del 2° ordine di a11(ovviamentea11deve essere ≠0 e h, k≥2.
Esempi di risoluzione
| 1 | 2 | 4 | 8 | 16 |
| 1 | 1 | 1 | 1 |
|
|
| 2 | 1 | 1 | 1 | 1 | 1 |
| 1 | 3 | 9 | 27 | 81 |
| 1 | 2 | 3 | 4 |
|
|
| 1 | 2 | 1 | 1 | 1 | 1 |
| 1 | 4 | 16 | 64 | 256 |
| 1 | 3 | 6 | 10 |
|
|
| 1 | 1 | 2 | 1 | 1 | 1 |
| 1 | 5 | 25 | 125 | 625 |
| 1 | 4 | 10 | 20 |
|
|
| 1 | 1 | 1 | 2 | 1 | 1 |
| 1 | 6 | 36 | 216 | 1296 |
|
| 1 | 2 | 3 |
|
|
| 1 | 1 | 1 | 1 | 2 | 1 |
|
| 1 | 5 | 19 | 65 |
|
| 2 | 5 | 9 |
|
|
| 1 | 1 | 1 | 1 | 1 | 2 |
|
| 2 | 12 | 56 | 240 |
|
| 3 | 9 | 19 |
|
|
|
| 3 | 1 | 1 | 1 | 1 |
|
| 3 | 21 | 117 | 609 |
|
|
| 1 | 3 |
|
|
|
| 1 | 3 | 1 | 1 | 1 |
|
| 4 | 32 | 208 | 1280 |
|
|
| 3 | 10 |
|
|
|
| 1 | 1 | 3 | 1 | 1 |
|
|
| 2 | 18 | 110 |
|
|
|
| 1 |
|
|
|
| 1 | 1 | 1 | 3 | 1 |
|
|
| 6 | 60 | 414 |
|
|
|
|
|
|
|
|
| 1 | 1 | 1 | 1 | 3 |
|
|
| 12 | 132 | 1020 |
| determinante= | 1 |
|
|
|
|
| 8 | 2 | 2 | 2 | ||
|
|
|
| 12 | 168 |
|
|
|
|
|
|
|
|
|
| 2 | 8 | 2 | 2 |
|
|
|
| 48 | 720 |
|
|
|
|
|
|
|
|
|
| 2 | 2 | 8 | 2 |
|
|
|
|
| 576 |
|
|
|
|
|
|
|
|
|
| 2 | 2 | 2 | 8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 60 | 12 | 12 |
|
| determinante= | 288 |
|
|
|
|
|
|
|
|
|
|
| 12 | 60 | 12 | ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 12 | 12 | 60 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 3456 | 576 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 576 | 3456 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 11612160 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| determinante= | 7 |
Con excel è possibile programmare in modo semplice il calcolo del determinante con questo metodo (vedi il file determinante con Chiò )
|
|




