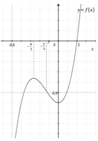
Funzione
Una relazione tra due insiemi A e B è una funzione se ogni elemento di A è associato a uno e un solo element di B. Per questo motivo una funzione si chiama anche corrispondenza unica. Una lettera minuscola (spesso la lettera ) si usa per indicare una funzione:
[math]y=f(x)[/math]
[math]f: A \rightarrow B[/math]
Si legge questa formulazione matematica come y uguale a f di x e la successiva come funzione f che va dall'insieme A all'insieme B.
Diciamo che A è l'insieme iniziale della funzione e B l'insieme finale.L'insieme di partenza A è chiamato il dominio della funzione; il sottoinsieme di B è formato dalle immagini degli elementi di A è detto codominio. y è l'immagine (o codominio) di utilizzando. Se l'espressione
[math]y=f(x)[/math]
contiene solo operazioni di addizione, sottrazione moltiplicazione, divisione, elevazione a potenza o estrazione di una radice, la funzione è algebrica.
Tipologia di funzioni
Una funzione algebrica in forma esplicita può essere di diverse tipologie. Qui di seguito un breve elenco di tipologie di funzioni:- Una funzione razionale intera (o polinomiale) se è espressa da un polinomio;
- Una funzione lineare se il polinomio è di primo grado rispetto alla variabile x;
- Una funzione quadratica se il polinomio in x è di secondo grado;
- Una funzione razionale fratta se è espressa per mezzo di quozienti di polinomi;
- Una funzione irrazionale se la variabile indipendente appare sotto il segno di una radice;
- Una funzione logaritmica se la variabile indipendente appare come argomento di logaritmo;
- Una funzione goniometrica se la variabile indipendente appare come argomento di funzione trigonometrica (seno, coseno, tangente...);
- Una funzione esponenziale se la variabile indipendente appare come esponente di un esponente (base qualunque o base neperiana).
Studio di funzione
Lo studio di una funzione ha come obiettivo finale quello di andare a tracciare il grafico sul piano cartesiano della funzione stessa. Come si traccia un grafico di una funzione?Ci sono diversi step che si devono necessariamente seguire per andare a tracciare il grafico della funzione. Gli step sono i seguenti riportati di seguito:
- Ricerca del dominio della funzione
- Ricerca dei punti di intersezione con gli assi cartesiani x e y del piano cartesiano della funzione
- Studio della positività della funzione
- Calcolo dei limiti della funzione
- Calcolo delle derivate della funzione e ricerca dei punti di massimo e di minimo
Dominio
Ricerca del dominio di una funzione si effettua andando a individuare il campo dell'esistenza in cui la funzione è definita. Se si ha una funzione polinomiale il campo di esistenza è tutto l'insieme dei reali. Se la funzione è una funzione fratta il campo di esistenza da ricercare deve prevedere che il denominatore sia diverso da zero. Se la funzione è un'esponenziale il campo di esistenza è tutto l'insieme dei reali. Se la funzione è un logaritmo il campo di esistenza da andare a definire deve prevedere che l'argomento della funzione logaritmica sia sempre maggiore di zero. Se la funzione è irrazionale con indice della radice positiva il campo di esistenza da ricercare deve prevedere che tutto quello che è sotto la radice deve essere posto maggiore o uguale a zero; invece se l'indice della radice è dispari allora il campo di esistenza è tutto l'insieme dei reali.
Intersezione degli assi
La ricerca per l'intersezione degli assi consiste nell'andare a imporre prima[math]y=0 [/math]
e poi [math]x=0[/math]
i risultati saranno corrispondenti ai punti di intersezione con gli assi.

Positività
LA ricerca della positività della funzione prevede di andare ad imporre che[math]f(x)>0[/math]
, facendo così sarà possibile andare a individuare dove la funzione risulta essere positiva e dove risulta essere negativa.
Limiti di una funzione
Il calcolo dei limiti di una funzione prevede di andare a studiare la funzione in quei punti di ambiguità in cui ad esempio il comportamento della funzione non si conosce come all'infinito agli estremi di definizione della funzione o in cui si ha una discontinuità della funzione.
Calcolo delle derivate e ricerca dei punti di massimo e di minimo
Affinché una funzione sia derivabile la funzione deve essere continua. Una funzione è continua se questa può essere tracciata sul foglio senza staccare la penna o interrompere il tratto di stesura. Questa è la definizione informale della continuità di una funzione. Di seguito verrà enunciata la definizione formale di continuità. Si consideri una funzione , e si voglia studiare la continuità della funzione. La funzione è definita continua in un punto se il limite della funzione per tendente al punto considerato è uguale al valore che la funzione assume ne punto stesso.Una funzione affinché sia derivabile deve risultare continua, per come è stato definito precedentemente. Esiste però un ulteriore vincolo affinché una funzione sia derivabile, ovvero che la derivata destra e la derivata sinistra debbano esistere ed essere uguali nel punto considerato. Se così non fosse la funzione non è derivabile.
Il calcolo delle derivate è utile per andare a studiare gli intervalli di crescenza e di decrescenza della funzione. Una volta calcolata la derivata prima si deve andare a porre maggiore o uguale a zero e risolvere la disequazione.
Se una funzione è sempre crescente non avremo dei punti di massimo o di minimo, lo stesso vale per le funzioni decrescenti.
In presenza di alternanza tra crescenza e decrescenza o viceversa si avranno dei punti di massimo o di minimo.
Si può ulteriormente effettuare una nuova ricerca di punti particolari relativamente ai punti di sella. Questi vengono individuati andando a calcolare la derivata seconda e ponendola maggiore e uguale a zero.
Grafico della funzione
Alla fine della raccolta di tutte queste informazioni sarà possibile andare a disegnare il grafico che è stato costruito passo per passo. Dapprima devono essere tagliate le parti in cui la funzione non è definita per il dominio, successivamente si individuano i punti di intersezione con gli assi, si procede poi a segnare dove la funzione risulta essere positiva e dove negativa, si osservano poi i comportamenti della funzione nei punti di ambiguità e si tracciano gli eventuali asintoti o comportamenti all'infinito individuati, infine si individuano nel grafico i punti di massimo e di minimo e di sella trovati, e dove la funzione cresce o decresce.