_stan
di _stan
(320 punti)
7' di lettura
Nel corso di tutta questa scheda considereremo due generiche iperboli
[math] H_O [/math]
ed
[math] H_V [/math]

[math] \displaystyle H_O:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \, \, \, \, \text{e} \, \, \, \, H_V:\frac{x^2}{a^2}-\frac{y^2}{b^2}=-1 [/math]

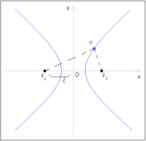
I fuochi della prima appartengono all'asse ?, mentre quelli della seconda giacciono sull'asse ?. Esse consentono di considerare al contempo tutte le iperboli riferite ai propri assi possibili.

Quando non ci saranno differenze, parleremo genericamente dell'iperbole ?.

Asintoti di un'iperbole

Osservazione 1: Consideriamo il rettangolo con i lati paralleli agli assi coordinati i cui assi di simmetria siano i semiassi trasverso e non trasverso di ?. In virtù della relazione
[math] c^2=a^2+b^2 [/math]
, che vale indipendentemente dall'orientazione dell'iperbole, risulta chiaro che le diagonali di detto rettangolo sono lunghe tanto quanto la distanza focale. Poiché esse passano per l'origine del sistema di coordinate, le rette cui appartengono hanno equazione del tipo (y=mx), e passano l'una per (?,?) e l'altra per (?,??), che sono due vertici consecutivi del rettangolo. Ciò porta a dire che le equazioni di tali rette sono

[math] \displaystyle \begin{equation}y=\pm\frac{b}{a}x \, \, \, \, \, \, \, \text{(1)}\end{equation} [/math]

Definizione 1: Asintoti.

Si chiamano asintoti di un'iperbole ? le rette date dalle equazioni

[math](1)[/math]
.

Osservazione 2: Per delimitare ulteriormente la parte di piano nella quale è contenuto il grafico di un'iperbole ?, faremo adesso vedere che esso è tutto contenuto in due dei quattro angoli in cui i suoi asintoti dividono il piano. Nel caso di

[math]H_O[/math]
, essi saranno gli angoli contenenti l'asse ?; nel caso di
[math]H_V[/math]
naturalmente varrà il viceversa.

Consideriamo a questo scopo una retta

[math]y=mx[/math]
passante per l'origine degli assi coordinati, e intersechiamola con
[math]H_O[/math]
. Avremo così

[math] \displaystyle \begin{cases}y=mx\\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\end{cases}\rightarrow \frac{x^2}{a^2}-\frac{m^2x^2}{b^2}=1\rightarrow[/math]

[math] \displaystyle \rightarrow \frac{x^2}{b^2}\Big(\frac{b^2}{a^2}-m^2\Big)=1\rightarrow x=\pm\frac{b}{\sqrt{\frac{b^2}{a^2}-m^2}}[/math]

Da questa scrittura risulta chiaro che se la radice quadrata esiste ed è distinta da 0, cioè

[math] \displaystyle m^2\lt\frac{b^2}{a^2}\rightarrow -\frac{b}{a}\lt m\lt\frac{b}{a}][/math]

allora l'iperbole s'interseca in due punti con la retta

[math]y=mx[/math]
, uno per ogni ramo. Qualora invece risultasse
[math] \displaystyle |m|\ge\frac{b}{a} [/math]
, non ci potrebbe essere alcuna intersezione; dunque l'iperbole non occupa alcun punto della parte di piano spazzata dalle rette i cui coefficienti angolari sono, in valore assoluto, maggiori di quelli degli asintoti, che sono
[math] m=\pm\frac{b}{a} [/math]
. Il grafico dell'iperbole è quindi, come volevasi, tutto compreso tra le rette
[math] y=\pm\frac{b}{a}x [/math]
.

Osservazione 3: Dall'osservazione 2 discende in particolare il fatto che un'iperbole non ha alcun punto d'intersezione con i suoi asintoti.

Osservazione 4: Quanto detto nell'osservazione 3 si può precisare ulteriormente, in modo tale da giungere alla seguente proprietà fondamentale: il grafico di un'iperbole si avvicina indefinitamente agli asintoti man mano che il generico punto della curva si allontana dall'origine.

Per provarlo consideriamo ancora l'equazione

[math] (2) [/math]
, questa volta per un punto generico ? appartenente a uno qualsiasi dei quattro quadranti, e modifichiamola nel modo seguente:

[math] \displaystyle y=\pm b\sqrt{\frac{x^2}{a^2}-1}\rightarrow y=\pm\frac{b}{a}x\sqrt{1-\frac{a^2}{x^2}} [/math]

È chiaro che al crescere di ?, cioè all'allontanarsi di ? dall'origine, il rapporto (a^2/x^2) si avvicina sempre più a zero; ciò porta il radicando, e dunque la radice, ad assumere valori indefinitamente vicini a 1. Più tale radice è simile a 1, più l'ordinata del punto ? è vicina a

[math] \pm\frac{b}{a}x [/math]
, che è l'ordinata del punto dell'asintoto avente la medesima ascissa di ?. Questo prova che, come volevamo, all'aumentare di ? i grafici dell'iperbole e dei suoi asintoti si avvicinano indefinitamente ma, come segue dall'osservazione 3, essi non si intersecano mai.

Grafico di un ramo dell'iperbole e del suo asintoto

Eccentricità dell'iperbole

Definizione 2: Eccentricità.

Si definisce eccentricità ? di un'iperbole il rapporto tra la distanza focale e l'asse trasverso.

Eccentricità dell'iperbole

Osservazione 5: Nel caso di un'iperbole i cui fuochi appartengono all'asse delle ?, essendo l'asse trasverso lungo 2?, l'eccentricità si calcola come ?=?/?. Nell'altro caso risulta naturalmente ?=?/?. Poiché per entrambe le iperboli è sempre vero che la distanza focale è maggiore dell'asse trasverso, necessariamente è verificata le disuguaglianza

[math] e \ge 1 [/math]
.

Osservazione 6: L'eccentricità è un parametro numerico che misura la "apertura" di un'iperbole. Nel caso limite ?=1 risulta che la distanza focale è uguale all'asse trasverso; poiché essi sono rispettivamente ipotenusa e cateto di un triangolo rettangolo il cui altro cateto è l'asse non trasverso, per il teorema di Pitagora segue che in questo caso la lunghezza dell'asse non trasverso è nulla. L'iperbole risulta dunque "appiattita" sull'asse cui appartengono i suoi fuochi, e consiste in null'altro che le due semirette di detto asse avente come origini i vertici dell'iperbole.

Se osserviamo poi cosa accade allorché ? assume valori sempre più grandi, cioè come si suole dire ? tende a infinito, ci accorgiamo che ciò significa, supposti fissi i vertici, che i rami dell'iperbole divengono sempre più rettilinei. Al limite, l'iperbole si riduce alle due rette parallele all'asse non trasverso passanti per i suoi vertici.

In entrambi i casi su considerati si dice che l'iperbole è degenere.

Altro materiale di supporto

Videolezione sulla iperbole

Esercizio proposto

Scritta l'equazione dell'iperbole riferita ai suoi assi di simmetria, avente per asse focale l'asse x, eccentricità
[math] \displaystyle e=\sqrt{\frac{3}{2}} [/math]
e passante per il punto
[math] P\Big(3;\frac{\sqrt{2}}{2}\Big) [/math]
. Determinare le equazioni delle due circonferenze aventi centro sull'asse y, tangenti agli asintoti dell'iperbole e aventi raggio
[math] \sqrt{6} [/math]
.

Trovi la soluzione nel forum di Matematicamente.it.

Vuoi approfondire Geometria - Formule e problemi di geometria con un insegnante esperto?
Trovalo su Ripetizioni.it