Equazioni letterali intere

Equazioni letterali intere

Le equazioni letterali intere in unincognita sono equazioni in cui, oltre alla lettera che rappresenta lincognita, appaiono altre lettere, dette parametri, che rappresentano quantit numeriche note, anche se non specificate.

Per esempio, le seguenti equazioni sono letterali intere, nell'incognita

:

Il calcolo letterale è utile per affrontare dei tipi di problemi in cui alcuni tipi di dato possono cambiare, cioè problemi in cui si può trovare una risoluzione generale che consente, una volta che siano noti i dati, di ricavare immediatamente la soluzione, senza dover ogni volta impostare un’equazione diversa.

Questi dati che possono cambiare vengono espressi mediante le lettere definite parametri.

Risoluzione di un'equazione letterale intera

Poiché i parametri sono sostanzialmente numeri, anche se non noti, la risoluzione delle equazioni letterali intere è molto simile a quella delle equazioni numeriche; valgono infatti i primi due principi di equivalenza delle equazioni e le loro conseguenze.
E possibile, quindi:

• Sommare o sottrarre una stessa quantità numerica ad ambo i membri dell’equazione ottenendo un’equazione equivalente a quella data (primo principio);
• Moltiplicare o dividere entrambi i membri dell’equazione per una stessa quantità numerica, diversa da zero, ottenendo un’equazione equivalente a quella data (secondo principio).

In relazione al secondo principio, ricordiamo che quando moltiplichiamo i membri dell’equazione per una quantità numerica contenente un parametro, dovremmo escludere i valori di quel parametro che fanno annullare la quantità numerica.

Risoluzione di un'equazione letterale intera

Ipotizziamo che, dopo diversi passaggi risolutivi, l'equazione si presenti nella forma:

dove

e possono essere numeri, monomi o polinomi, eventualmente espressi nelle lettere che rappresentano i parametri.
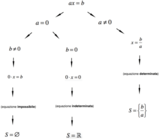
Esaminiamo ora due casi:

1. Se
   [math]A[/math]
   un numero diverso da zero, si trova immediatamente la soluzione: si dividono entrambi i membri per
   [math]A[/math]
   e si trova la soluzione nella forma
   [math]x = A/B[/math]
   ;
2. Se
   [math]A[/math]
   un monomio o un polinomio, si determinano gli eventuali valori dei parametri per cui lespressione si annulla, e si procede poi alla discussione.

Discutere unequazione letterale della forma significa determinare i valori dei parametri per cui lequazione risulta determinate, indeterminata o impossibile.

Esempio di discussione di unequazione letterale

Consideriamo la seguente equazione letterale in incognita

:

Per ridurla nella forma sopra descritta, svolgiamo alcuni passaggi:

Ora notiamo che

ha come coefficiente ; poichè non ci viene detto nulla riguardo questa lettera, essa potrebbe assumere qualsiasi valore; in particolare, può essere uguale a zero.
Consideriamo allora i seguenti due casi:

1. [math]\space b=0[/math]
   : sostituiamo questo valore di
   [math]b[/math]
   al parametro
   [math]b[/math]
   dell'equazione:
   
   [math]\begin{gather*}0 \cdot x=0-3 \\ 0=-3 \end{gather*}[/math]
   otteniamo un'uguaglianza falsa; di conseguenza, per questo valore di
   [math]b[/math]
   l'equazione risulta impossibile.
2. [math]\space b \neq 0[/math]
   : in questo caso, possiamo determinare il risultato dellequazione dividendo entrambi i membri per il coefficiente di
   [math]x[/math]
   , ottenendo:
   [math]x=\frac{b-3}{b}[/math]

Condizioni di esistenza

Nelle equazioni in cui compaiono frazioni i cui denominatori sono costituiti da espressioni letterali, è necessario imporre delle condizioni che ci garantiscano che il denominatore delle frazioni non si annulli. Per esempio, nel caso in cui abbiamo un'equazione di questo tipo:

dobbiamo porre , quindi .
Queste ipotesi vengono chiamate condizioni di esistenza (e si indicano ) dell'equazione. Per i valori dei parametri che soddisfano le condizioni di esistenza, tutti i denominatori risultano diversi da zero, ed è quindi possibile applicare il secondo principio di equivalenza.

Equazioni letterali frazionarie

Le equazioni letterali frazionarie sono equazioni letterali in cui compaiono incognite al denominatore.

Ecco alcuni esempi di equazioni letterali frazionarie:

Per risolvere questo tipo di equazione si procede tenendo conto delle regole riguardanti le equazioni intere frazionarie, e le equazioni letterali, anche se per questo tipo di equazioni la verifica non risulta sempre immediata. Infatti, sia le condizioni di accettabilità che le soluzioni dell'equazione possono essere rappresentate da espressioni letterale che, pur essendo differenti nella forma, possono coincidere per qualche valore del parametro. Per questo, sarà necessario eseguire anche la discussione dell'accettabilità delle soluzioni trovate.

Vediamo il seguente esempio:

Poniamo le condizioni di accettabilità (riguardanti la

) e le condizioni di esistenza (riguardanti il parametro):

Possiamo procedere calcolando il

dei denominatori, sommando le frazioni e svolgendo i calcoli, fino ad arrivare ad avere l'equazioni della forma :

Effettuiamo ora la discussione di questa equazione:

• se
  [math]m = 3[/math]
  si ha:
  [math]0 = 3[/math]
  , quindi l'equazione è impossibile;
• se
  [math]m[/math]
  è diverso da 3, ricaviamo
  [math]x[/math]
  dall'equazione:
  [math]x=\frac{m}{m-3}[/math]

Notiamo, quindi, che le condizioni di accettabilità e la soluzione dell'equazione sono rappresentate da espressioni diverse, ma per , esse sono uguali. Quindi, per , troviamo , che è un valore che non può essere accettato, perché escluso dalle condizioni di accettabilità.
Possiamo quindi riassumere:
;
;