Testo del problema
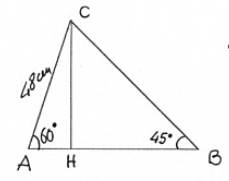
Nel triangolo scaleno[math]ABC[/math]
i due angoli alla base misurano rispettivamente [math]45^{\circ}[/math]
e [math]60^{\circ}[/math]
. Sapendo che il lato [math]AC[/math]
misura [math]48 cm[/math]
, calcola perimetro e area del triangolo.
Risoluzione 1 del triangolo scaleno: metodo sintetico
Prendiamo sul segmento[math]AB[/math]
il punto [math]H[/math]
, tale che [math]CH[/math]
sia l'altezza del triangolo relativa alla base [math]AB[/math]
. Osserviamo che il triangolo [math]ACH[/math]
è metà di un triangolo equilatero, dal momento che l'angolo in [math]A[/math]
misura [math]60^{\circ}[/math]
. Similmente, [math]CHB[/math]
è metà di un quadrato poiché l'angolo in [math]B[/math]
misura [math]45^{\circ}[/math]
, ossia il medesimo angolo che "stacca" la diagonale di un quadrato. Esaminiamo prima il triangolo [math]ACH[/math]
: [math]AC = 48 \text{cm}[/math]
, [math]AH=\frac{1}{2}AC = 24\text{cm})[/math]
(perché per quanto detto prima si ha che [math]AH[/math]
è la metà di [math]AC[/math]
). Applicando il Teorema di Pitagora (il quale enuncia che il quadrato costruito sull'ipotenusa è uguale alla somma dei quadrati costruiti sui due cateti) al triangolo [math]ACH[/math]
si ricava [math]CH=\sqrt{48^2-24^2}=41.57\text{cm}[/math]
Consideriamo ora il triangolo [math]CHB[/math]
: abbiamo ricavato prima che [math]CH = 41.57\text{cm}[/math]
ed essendo [math]HB=CH[/math]
poiché [math]CHB[/math]
è la metà di un quadrato, applichiamo nuovamente il teorema di Pitagora per ricavare [math]CB[/math]
. Allora otteniamo che [math]CB=\sqrt{41.57^2+41.57^2}=58.79 \text{cm}[/math]
. Ora abbiamo dati sufficienti per il calcolo del perimetro e dell'area:Perimetro:
[math] 2p=(48 + 24 + 41.57 + 58.79)\text{cm} = 172.36\text{cm}[/math]
Area:
[math]\frac{AB \cdot CH}{2} = \frac{(24+41.57)\cdot 41.57}{2}\text{cm}^2[/math]
, circa [math]1362,87\text{cm}^2)[/math]
Risoluzione 2 del triangolo scaleno: metodo trigonometrico
Prendiamo sul segmento[math]AB[/math]
il punto [math]H[/math]
, tale che [math]CH[/math]
sia l'altezza del triangolo relativa alla base [math]AB[/math]
. Allora possiamo dire che [math]AH=AC \cdot \cos(60^{\circ})[/math]
, dato che nel triangolo [math]ACH[/math]
, [math]AH[/math]
è il cateto adiacente a tale angolo. Per ragioni analoghe, possiamo inoltre affermare che [math]BH=CB \cdot \cos(45^{\circ})[/math]
.Per determinare
[math]CB[/math]
si può fare riferimento al teorema dei seni, il quale enuncia che il rapporto tra la misura di un lato e il seno dell'angolo ad esso opposto è costante.Possiamo quindi scrivere:
[math]AC:\sin(45^{\circ})=BC:\sin(60^{\circ})[/math]
, da cui si ricava che [math]BC=\frac{AC \cdot \sin(60^{\circ})}{\sin(45^{\circ})}[/math]
, da ciò ricaviamo che [math]BC[/math]
vale circa 58,79 cm.In definitiva ricaviamo anche il lato
[math]AB[/math]
, pari a [math]AB=AH+BH=AC \cdot \cos(60^{\circ})+AB \cdot \cos(45^{\circ})[/math]
cioè circa 65,57 cm.Infine calcoliamo
[math]CH=AC \cdot \sin(60^{\circ})[/math]
(poiché questa volta facciamo riferimento al cateto opposto. Calcolando tale prodotto troviamo che [math]CH[/math]
è lungo circa 41,57 cm.Per approfondimenti su seno e coseno, vedi anche qua
Adesso abbiamo dati sufficienti per trovare il perimetro e l'area del triangolo
[math]ABC[/math]
.Perimetro:
[math] 2p=(48 + 65.57 + 58.79)\text{cm} = 172.36\text{cm}[/math]
Area:
[math]\frac{AB \cdot CH}{2} = \frac{(65.57)\cdot 41.57}{2}\text{cm}^2[/math]
, circa [math]1362,87\text{cm}^2)[/math]
.