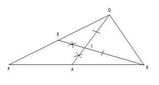
Sia
[math]E[/math]
un punto esterno a una data circonferenza di centro [math]O[/math]
; un angolo di vertice [math]E[/math]
ha i lati secanti la circonferenza. Siano [math]A[/math]
e [math]B[/math]
le intersezioni del primo lato dell'angolo con la circonferenza (con [math]ar{AE}ar{BE}[/math]
) e [math]C[/math]
e [math]D[/math]
le intersezioni del secondo lato (con [math]\bar{CE}). Dimostrare che
[math]hat(BED)=1/2(hat(BOD)-hat(AOC))[/math]
Dopo aver fatto un disegno, osserviamo la figura.
Gli angoli alla circonferenza godono di importanti proprietà : in questo caso ricordiamo che se un angolo alla circonferenza insiste su un certo arco, allora sarà la metà di un angolo al centro che insiste sull'arco medesimo.
In virtù di questo, possiamo dire
[math]hat{BAD}=1/2hat{BOD}[/math]
, poiché angolo alla circonferenza e angolo al centro che sottendono lo stesso arco BD.
[math]hat{ADE}=1/2hat{AOC}[/math]
poiché angolo alla circonferenza e angolo al centro che sottendono lo stesso arco AC Poi, consideriamo il triangolo
[math]\stackrel(Delta)(AED)[/math]
e l'angolo esterno [math]hat{BAD}[/math]
. Per il teorema dell'angolo esterno, ogni angolo esterno di un triangolo è congruente alla somma degli angoli interni ad esso non adiacenti.
Quindi risulta essere
[math]hat{BAD}=hat{AED}+hat{ADE}[/math]
, da cui [math]hat{AED}=hat{BAD}-hat{ADE}[/math]
. Ora sostituiamo le espressioni trovate precedentemente, nell'ultima relazione.
Otteniamo
[math]hat{AED}=1/2hat{BOD}-1/2hat{AOC}[/math]
, e raccogliendo [math]1/2[/math]
ottieniamo la tesi. FINE