Fisica 2 - Applicazione Legge di Ampere

[strano666]

Se ho difficoltà nel trovare la \( q_{int} \) per la legge di gauss, immaginateci per la corrente concatenata nella legge di ampere

Tra due piani \( x=-h \) e \( x=h \), di un sistema di riferimento cartesiano, scorre nella direzione dell'asse z una corrente con densità \( J=J_{0}\, cos\left ( \frac{\pi x}{2h} \right ) \) . Si chiede di determinare il campo magnetico generato in tutto lo spazio.

Utilizzo una simmetria cilindrica tangente e vado quindi a calcolarmi la corrente concatenata \( i_{cc} \)
Parto dalla situazione in cui \( -h<x<h \) , quindi ho scritto che:
\( i_{cc}=\int_{0}^{r} J_{0}\, cos\left ( \frac{\pi x}{2h} \right )\: 2\pi x \: dx \)

Dopodichè per trovarmi la corrente concatenata nel caso in cui \( x<-h \) e \( x>h \) varierei gli estremi di integrazione, facendoli variare da \( 0 \) ad \( h \) .

Ovviamente dopo aver trovato la corrente concatenata tutto è più semplice applicando la legge di ampere, \( \oint \vec{B}\cdot d\Sigma = \mu _{0}\, i_{cc} \)

Quanti errori?

[RenzoDF]

Utilizzo una simmetria cilindrica tangente e vado quindi a calcolarmi la corrente concatenata \( i_{cc} \)
Parto dalla situazione in cui \( -h<x<h \) , quindi ho scritto che:
\( i_{cc}=\int_{0}^{r} J_{0}\, cos\left ( \frac{\pi x}{2h} \right )\: 2\pi x \: dx \)

Scusa ma non capisco dove tu veda questa simmetria cilindrica.

Io direi che la geometria dovrebbe essere planare

fig.1

Creato con FidoCadJ | Visualizza codice

e visto che i piani sono implicitamente infiniti, le linee di forza a destra e a sinistra dei piani saranno linee rette, parallele al piano con versi opposti sui due lati.
Basterà quindi tracciare un rettangolo con un lato di lunghezza L sull'asse y e l'altro con generica lunghezza x parallelo all'omonimo asse per capire che basta anche in questo caso, una semplice relazione scalare per ottenere il campo magnetico H

$\oint_{l}^{ } \vec{H}\cdot \vec{dl}=I_{conc}(x) \qquad\rightarrow \qquad\vec{H}(x)=\frac{I_{conc}(x)}{L}\hat{u}_y$

risultato notevole per $ | x |>h$ duale alla corrispondente geometria in elettrostatica, ma anche facilmente
ricavabile per $ | x |<h$ attraverso una semplice integrazione.

[strano666]

Mi scuso subito per il disegno approssimativo, ma Fidocad tramite applet non mi dava tutte le opzioni.
Io avevo utilizzato la simmetria cilindirca, probabilmente sbagliando, in questo modo:

Schema elettrico

Creato con FidoCadJ | Visualizza codice

Vedendo il tutto dall'alto, con l'asse Z, e quindi la corrente, uscente dallo schermo. Facendo così variare il raggio del cilindro. Come mai non è possibile ragionare così? Non sarebbe la stessa cosa di un rettangolo con la L fissa?

Studiandolo come mi hai suggerito tu non mi troverei con lo stesso integrale che ho scritto prima, ossia
\( I_{conc}= \int_{0}^{x}x\: J_{0} \: cos\left ( \frac{\pi x }{2h} \right )\; ,\; con \; 0<x<h \)

Ti ringrazio veramente molto per il tempo che mi stai dedicando, anche con Gauss

[RenzoDF]

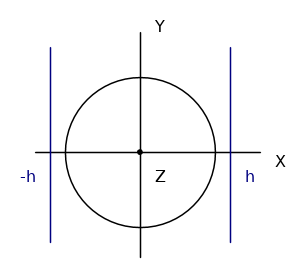
Vedendo il tutto dall'alto, con l'asse Z, e quindi la corrente, uscente dallo schermo.

Ovviamente, come ho anch'io indicato nel mio disegno.

Facendo così variare il raggio del cilindro. Come mai non è possibile ragionare così? Non sarebbe la stessa cosa di un rettangolo con la L fissa?

Scusa, ma il il cilindro non riesco a capire da dove lo tiri fuori, un percorso circolare come quello da te disegnato lo puoi di certo fare, ma andrai solo a complicarti la vita in quanto nei vari punti di quella circonferenza il campo H sarà diverso, così come diverso sarà il suo angolo rispetto alla tangente.

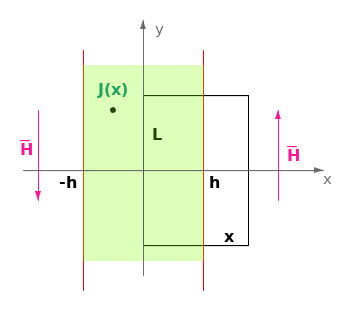
Quello che faccio io è partire dal fatto che per la simmetria planare conosco l'andamento delle linee di forza, ovvero il loro parallelismo ai piani, per andare ad integrare H lungo lungo un percorso chiuso che sia parallelo a dette linee o ortogonale alle stesse; ecco il perché del rettangolo.

In questo modo, l'unico contributo alla circuitazione su $l$ sarà quello relativo al lato del rettangolo che non appartiene all'asse del sistema, che porta quindi al semplice prodotto fra $H$ e $L$; andando poi a calcolare la corrente concatenata a $l$ dall'integrale della densità relativa alla superficie $S$ che la ha per bordo, avremo che dalla relazione generale di Ampere,

$\oint_{l}^{ }\vec{H}\cdot \vec{text(d)l} =\int_{S}^{ }\vec{J}\cdot \vec{text(d)S}=I_{conc}$

grazie alle suddette semplificazioni, integrando i contributi delle varie correnti infinitesime nelle $text(d)S=L \ text(d)x$ relative alla generica ascissa x

$HL=\int_{0}^{x}J(x)L \ text(d) x=\int_{0}^{x}J_0cos(\frac{\pi x}{2h})L \ text(d) x$

ed infine

$\vec{H}=\frac{2h J_0 }{\pi }sin(\frac{\pi x}{2h})\hat{u}_y$

Questo, ovviamente per i punti interni, ovvero per $|x|<h$, in quanto per $|x|>h$, il campo H sarà costante in tutto lo spazio, "saturando" a

$\vec{H}=\frac{2h J_0 }{\pi }sgn(x)\hat{u}_y$