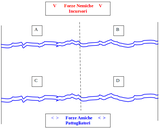
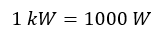(90 punti)

8' di lettura

3,5 / 5 (2)

In una zona montuosa delle Alpi viene costruita una grande diga, mediante creazione di un lago artificiale, allo scopo di alimentare una centrale idroelettrica. Supponiamo che il lago sia schematizzabile come un parallelepipedo rettangolo. La diga è a forma di parabola, con la convessità che penetra all'interno del lago, come nella figura (fonte Wikipedia).

Nel disegno sotto schematizziamo la diga ed il lago

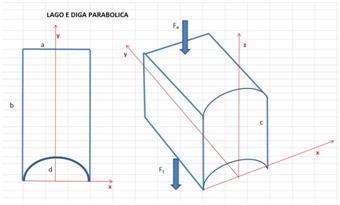
Come è noto la tenuta della diga non è perfetta, perché possono avvenire trafilamenti di acqua attraverso il fondo del lago, che non è impermeabile: nel nostro caso la portata di acqua perduta per trafilamento è rappresentata dalla seguente equazione:

[math]Q_t = k_1 \cdot z[/math]

,dove z è il livello (variabile) dell'acqua nel lago.

Per collaudare la diga si inizia il riempimento con un flusso

[math]Q_e[/math]

di portata costante. Le portate sono volumetriche e quindi sono espresse in

[math]m^3/s[/math]

.
Desideriamo calcolare il tempo necessario a riempire il lago fino al livello di progetto

[math]z_c[/math]

A questo scopo è necessario cominciare a calcolare il volume del lago quando ha raggiunto il livello finale

[math]z_c[/math]

. Il volume è dato dal prodotto della superficie del lago per l'altezza dell'acqua

[math]z_c[/math]

.
La superficie S si determina come differenza tra la superficie di base del parallelepipedo che contiene il lago e l'area compresa tra l'arco di parabola e l'asse x.
La superficie di base del parallelepipedo vale:

[math]A_b=ab[/math]

Se a,b,c sono le tre dimensioni del parallelepipedo, la parabola che forma la diga è data dalla funzione:

[math]y=d(1- 4/a^2 x^2)[/math]

L'area sotto la parabola vale:

[math]A_p = 2dâˆ«_0^{a/2} (1- 4/a^2 x^2)dx[/math]

La cui funzione integranda è data da:

[math]x - 4/(3a^2 ) x^3[/math]

e quindi sostituendo si ottiene:

[math]A_p= 2/3 ad[/math]

In definitiva la superficie del lago è:

[math]S=A_b - A_p= a (b-2/3 d)[/math]

Il volume del lago pieno vale:

[math]V = cS = (az_c) (b-2/3d)[/math]

Ora vogliamo calcolare il tempo necessario per riempire il lago. Dovremo fare un bilancio materiale: la variazione di volume divisa per il tempo eguaglia la differenza tra la portata di alimentazione e quella di trafilamento. Il bilancio va fatto su quantità infinitesime:

[math](dV)/(dt) = Q_e - Q_t[/math]

Notiamo che l'equazione sopra scritta è dimensionalmente corretta: infatti

[math](dV)/(dt)[/math]

ha le dimensioni di un volume diviso per un tempo, quindi

[math]m^3/s[/math]

. Le portate sono espresse in

[math]m^3/s[/math]

Ora se prendiamo una fettina (infinitesima) di lago compresa tra due piani orizzontali, rispettivamente a quota z e z+dz , il volume dV risulta pari a

[math]dV = Sdz[/math]

Quindi otteniamo:

[math](dV)/(dt)= S dz/dt= Q_e - Q_t[/math]

E ricordando che

[math]Qt = k \cdot z[/math]

diventa:

[math]S dz/dt= Q_e - kz[/math]

Che con una semplice divisione diventa:

[math]dz/( Q_e- kz) = dt/S[/math]

Abbiamo ora due semplici integrali:

[math]âˆ«_0^{z_c} dz/( Q_e - kz) = 1/S âˆ«_0^{t_c} dt[/math]

Facilmente calcolabili:

[math]ln (( Q_e - kz_c)/ Q_e) = ln(1-(kz_c)/ Q_e ) = - k/S t_c[/math]

Quindi

[math]t_c=-S/k ln(1-(kz_c)/ Q_e )[/math]

Quando il lago è in condizione di regime, vale a dire ha raggiunto il livello di progetto, la portata di trafilamento diventa costante e vale

[math]Q_(t,reg)= -kz_c[/math]

Mentre il bilancio dei flussi è dato da

[math]Q_reg= Q_e-Q_(t,reg) = Q_e- kz_c[/math]

Ora desideriamo calcolare la spinta che il lago esercita sulla diga. La spinta è una forza e si ottiene, dimensionalmente, come prodotto della pressione per la superficie sulla quale si esercita la pressione. Nel nostro caso la pressione non è uniforme ma varia con la quota z secondo la legge di Stevino:

[math]p = Ïg(z_c-z)[/math]

. E' dunque massima sul fondo del lago e nulla in superficie.

Il calcolo della spinta su una superficie curva (l'arco della diga) non è semplice. Si usa un piccolo accorgimento. Si considera un pezzetto di lago compreso tra l'arco della diga ed un piano parallelo al piano xz che taglia il lago ad una distanza qualsiasi dall'arco (come da disegno sotto).

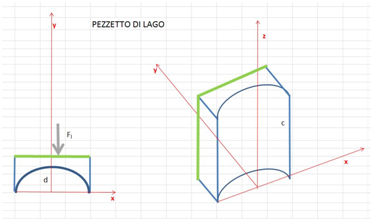
Perché questo pezzetto di lago resti in equilibrio è necessario che la spinta esercitata dalla diga sul lago in direzione y sia uguale e contraria alla spinta che il resto del lago esercita sul pezzetto di lago. In definitiva la spinta (Fs) del resto del lago sul rettangolo verde (disegno sotto) che delimita il pezzetto di lago eguaglia la spinta che il lago esercita sulla diga.

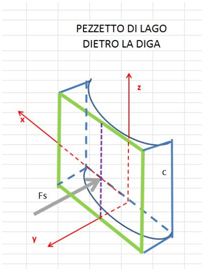
Si prende ora una fettina di lago compresa tra due piani paralleli al piano xy e distanti tra loro dz e si considera, a quota z, la striscia di superficie

[math]a \cdot dz[/math]

(disegno sotto). Su questa striscia la pressione vale p (vettore color mattone, in figura) ed è uniforme su tutta la striscia.

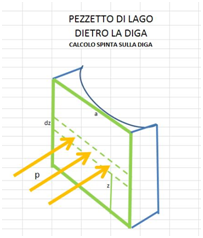
Quindi la forza esercitata sulla striscia vale:

[math]p \cdot a \cdot dz = aÏg(z_c-z)dz[/math]

Non resta ora che da integrare per ottenere

[math]F_s[/math]

(la spinta del lago sulla diga):

[math]F_s=âˆ«_0^{z_c} aÏg(z_c-z)dz= (aÏgz_c^2)/2[/math]

Last but not least desideriamo individuare il punto in cui si applica la spinta

[math]F_s[/math]

.
Per far questo calcoliamo il momento della spinta sul rettangolo verde. Si tratta, ancora una volta di un bilancio differenziale. Basta moltiplicare la spinta infinitesima per il braccio z (come riportato nella figura sopra).
Quindi

[math]dM_s= [aÏg(z_c-z)dz] \cdot z[/math]

Ed integrare sull'intero rettangolo:

[math]M_s=aÏg âˆ«_0^{z_c}z(z_c-z)dz= (aÏgz_c^3)/6[/math]

Ora per definizione il momento della spinta è dato dal prodotto della spinta

[math]F_s[/math]

per braccio

[math]z_S[/math]

, quindi:

[math]M_s=F_s z_S[/math]

In definitiva:

[math]z_S=M_s/F_s = ( (aÏgz_c^3)/6 )/((aÏgz_c^2)/2) = z_c/3[/math]

Dunque il centro di spinta del lago sulla diga è situato sott'acqua, ad un terzo del livello del lago (partendo dal fondo).
Il file EXCEL allegato riporta i dati ed tutti i calcoli relativi alle formule fin qui sviluppate.

Diga
Il file Excel del problema della diga.