Forza gravitazionale, interazione Sole e Terra

In questo appunto parliamo della Legge di gravitazione universale e del sistema Sole-Terra. Vedremo come costruire un modello matematico non troppo complicato per descrivere il moto di rivoluzione della Terra attorno al Sole senza considerare l’effetto degli altri pianeti e trascuriamo a tal fine anche la Luna. Di sicuro il nostro satellite influisce sulle maree terrestri, ma ha ben poco effetto gravitazionale sul moti del pianeta, data la grande differenza di massa.

Forza gravitazionale

La Terra fa parte del sistema solare, insieme ad altri pianeti che orbitano attorno alla stella a distanze grandi e molto diverse. In linea di principio tutti i pianeti si attraggono tra di loro e sono attratti dal Sole, ma le attrazioni pianeta-pianeta sono molto piccole rispetto alle attrazioni pianeta-Sole.
L'attrazione gravitazionale, sappiamo, è quantificata con ottima precisione dalla legge di gravitazione universale di Isaac Newton, il quale non solo la scoprì, ma la dimostrò.
Il modulo della forza, per il sistema Terra Sole, è cosi esprimibile:

dove

ed sono rispettivamente le masse di Terra e Sole, mentre è la distanza tra i baricentri dei due corpi celesti, la costante di gravitazione universale.

La forza

è attrattiva ed è diretta lungo la congiungente dei baricentri. Per il terzo principio della dinamica la forza con la quale la Terra attrae il Sole è uguale e contraria a quella con cui il Sole attrae la Terra. Le due forze ovviamente non si annullano perché sono applicate a corpi diversi. I due corpi celesti sono liberi di muoversi, la forza gravitazionale produce il moto per ognuno dei due, sulla base del secondo principio della dinamica:

dove

è l'accelerazione, che è la derivata della velocità rispetto al tempo.

Combinando le equazioni (1) e (2) si ottiene:

L'equazione (3) descrive il moto della Terra.

Un'equazione del tutto analoga si applica al moto del Sole, per via dell'attrazione della Terra. Tuttavia l'attrazione terrestre ha un effetto trascurabile sul Sole data l'enorme sproporzione tra le masse dei due corpi

. Possiamo quindi assumere che il Sole resti immobile e si possa considerare con buona approssimazione un riferimento inerziale.

Sappiamo che la Terra ruota attorno al Sole (moto di Rivoluzione) su di un orbita ellittica, che giace in un piano (in azzurro nella figura seguente).

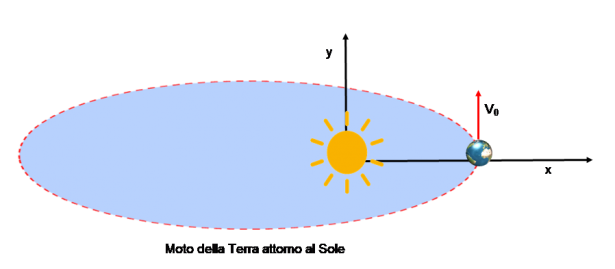
Il disegno rappresenta la posizione del pianeta a inizio dell'anno, quando si trova al perielio, il punto più vicino al Sole. La rappresentazione non è in scala ed è deformata per evidenziare la forma ellittica, mentre in realtà l'orbita è molto vicina ad una circonferenza, come si vede nel disegno sotto in scala, dove il Sole è nell'origine.

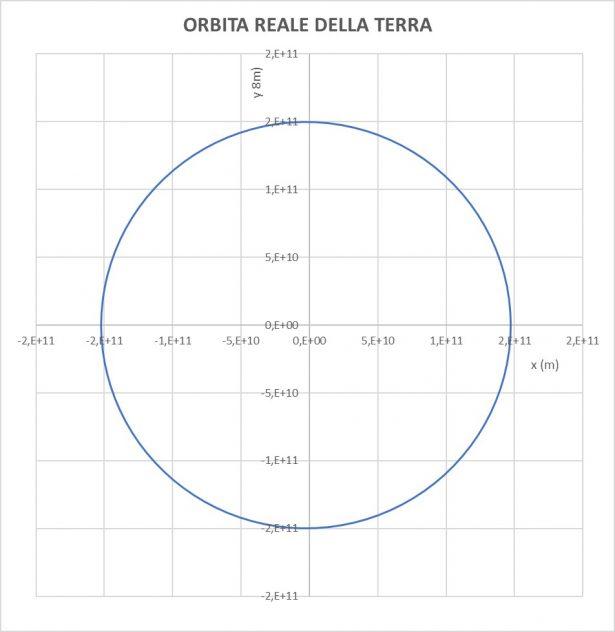
Conosciamo la distanza Terra-Sole al perielio ed anche la velocità

, pari a circa 30 mila m/s. La velocità di rivoluzione è leggermente variabile lungo l'orbita ed è massima al perielio.

Campo gravitazionale, richiami teorici

È opportuno ricordare che il campo gravitazionale è di tipo conservativo, questo vuol dire che è possibile definire l'energia potenziale del campo gravitazionale, che si ottiene integrando l'equazione (1) lungo la distanza d, ottenendo:

Il lavoro dal campo gravitazionale fatto lungo un cammino chiuso (

) è nullo, vale a dire non ci sono dissipazioni di energia; in un campo gravitazionale vale il principio di conservazione dell’energia meccanica E, data dalla somma di energia potenziale U ed energia cinetica K:

Nel nostro modello semplificato di sistema solare ogni variazione di

è compensata da una variazione uguale e contraria di e viceversa.
È stato dimostrato che l'orbita di un corpo celeste, nel suo moto attorno ad un altro di massa enormemente maggiore, è di tipo diverso secondo il valore dell'energia come da tabella seguente:

VALORE DELL'ENERGIA	ORBITA	ECCENTRICITA'
E	ELLISSE
E = 0	PARABOLA	= 1
E > 0	IPERBOLE	> 1

Velocità della Terra al perielio

Nel caso della Terra al perielio risulta e questo conferma che l'orbita della Terra è ellittica.
Nel nostro modello semplificato Terra-Sole l'orbita della Terra è perfettamente stabile, come si può verificare calcolando la sua orbita anche in tempi lunghi dopo moltissime rotazioni. In realtà la Terra fa parte del sistema solare ed esistono delle azioni gravitazionali (piccolissime) da parte degli altri pianeti che influenzano leggermente l'orbita terrestre e che abbiamo trascurato. Supercomputer moderni, con modelli di calcolo molto precisi hanno verificato la sua stabilità, almeno per alcuni milioni di anni futuri. È anche vero che per effetto degli altri pianeti l'eccentricità dell'orbita terrestre varia leggermente (in modo periodico) nell' arco di decine di migliaia di anni come riportato nel diagramma seguente (Fonte Wikipedia).

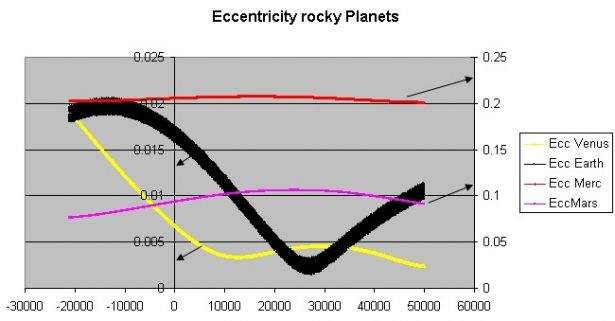
(Fonte della figura: Data generated with Gravity Simulator written by Tony Dunn. Source JPG on server)

Ora vogliamo a fare qualche nuova simulazione facendo l'ipotesi che la velocità della Terra al perielio sia un po' diversa, vale a dire un po' minore o maggiore. La simulazione prenderà in considerazione tre casi:

• ipotesi di un’orbita perfettamente circolare,
• ipotesi di una riduzione della velocità cosmica,
• ipotesi di un aumento della velocità cosmica.

Variazione della velocità cosmica

Ipotesi uno: Orbita circolare
In questo caso l'attrazione gravitazionale sarebbe esattamente bilanciata dall’accelerazione centripeta:

e quindi:

Alla distanza del Perielio Terra-Sole si avrebbe

, costante lungo tutta l'orbita circolare.

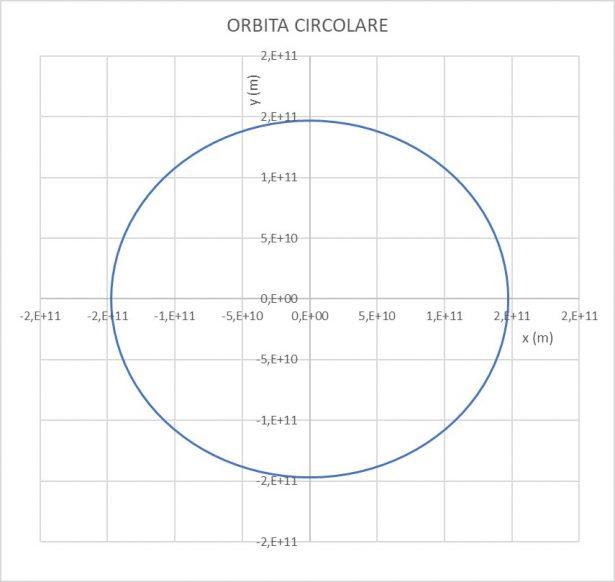
Questa velocità tipica si definisce prima velocità cosmica e, come appare dalla (7), non dipende dalla massa del pianeta che orbita attorno al Sole, ma solo dalla sua distanza. L'anno durerebbe 356 giorni, una piccola differenza rispetto al valore reale. Si chiama prima velocità cosmica perché è la velocità minima che consente al pianeta di restare in orbita attorno al Sole. A velocità inferiore precipita sulla nostra stella con un moto spiraliforme. La velocità reale della Terra al perielio è di circa 30,3 mila m/s e quindi differisce dalla prima velocità cosmica

per l'1%. Questo è dovuto alla sua piccolissima eccentricità.

Ipotesi 2: riduzione della velocità al perielio
Che cosa succederebbe se la velocità della Terra al perielio dovesse ridursi al disotto di 30 km/s? Evidentemente precipiterebbe verso il Sole. Proviamo a simulare questo moto nell'ipotesi

.

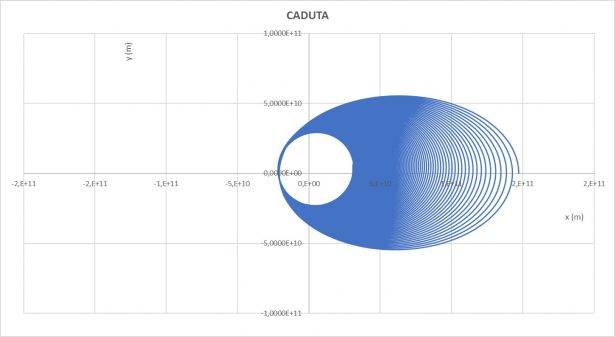
Il diagramma riporta il moto della terra a partire dal perielio (a destra) in una spirale antioraria (si suppone di osservare la Terra dal polo Nord). L'origine degli assi è il baricentro del Sole. Il calcolo si riferisce ad una durata di 16 anni. Continuando i calcoli, dopo circa un altro anno si avrebbe il collasso dentro il Sole. Il calcolo è stato effettuato ad una velocità metà di quella reale per drammatizzare il risultato.
Tuttavia l'esito finale sarebbe lo stesso, ma con tempi molto più lunghi, in caso di V0 di poco inferiore alla prima velocità cosmica.
Qui sotto è schematizzato l'impatto Terra-cometa al Perielio, quando entrambi i corpi si muovono lungo l'asse y.

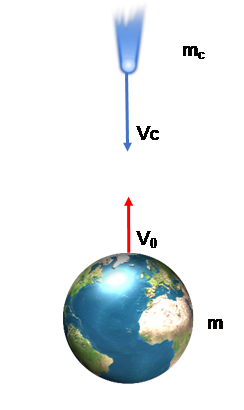
Ipotesi 3: aumento della velocità della Terra
Se la velocità

fosse superiore a quella attuale si avrebbe un'orbita ellittica molto più eccentrica. Ecco un esempio dell'orbita per un aumento del 10% di :

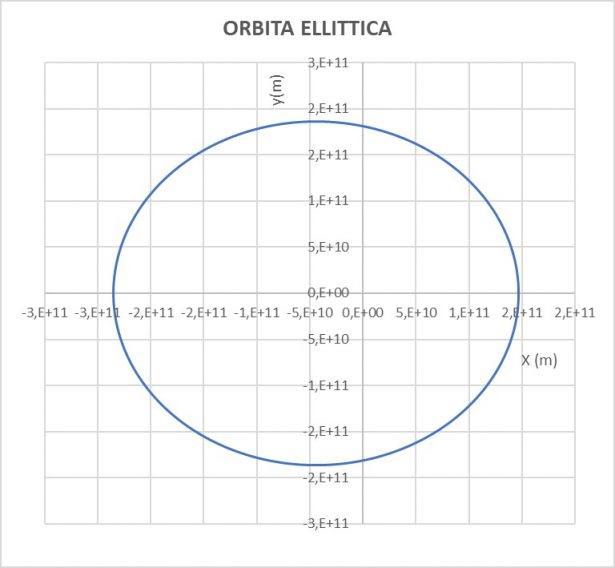
In questa situazione il semiasse dell'orbita ellittica aumenterebbe del 28% e l'anno durerebbe 527 giorni. Questo cambierebbe moltissimo il ciclo delle stagioni e le condizioni climatiche.

Velocità limite, velocità di fuga

Si avrebbe sempre orbita ellittica per ogni velocità superiore? La risposta è negativa. Esiste una ulteriore velocità limite, la seconda velocità cosmica, che si determina azzerando l'energia E, equazione (5), ottenendo:

Vale a dire:

Questo vuol dire che al perielio si avrebbe

.

In questa situazione (

), come abbiamo visto nella tabella precedente, l'orbita diventa parabolica, con il Sole nel fuoco della parabola. In questo caso la Terra partendo dal perielio si allontanerebbe gradualmente dal Sole dirigendosi all'infinito nel cosmo.

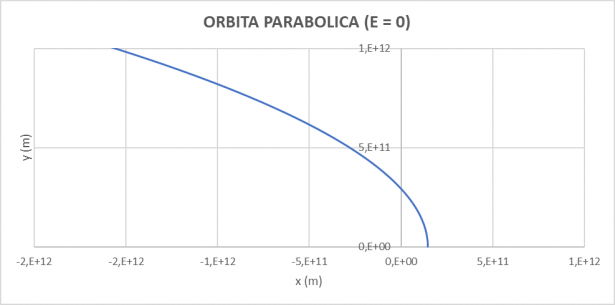
Orbita iperbolica

Infine quando è superiore alla seconda velocità cosmica il moto della terra sarebbe simile alla precedente da un punto di vista qualitativo, ma l'orbita sarebbe un'iperbole ().

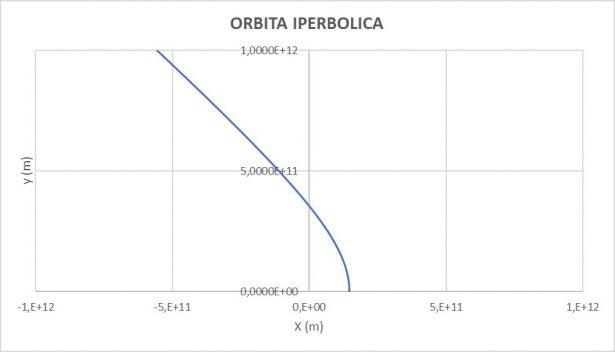
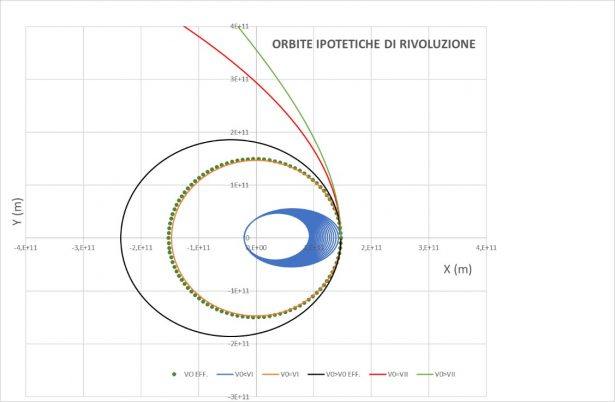
Il seguente diagramma descrive le orbite. Dall'interno all'esterno aumenta la velocità al perielio:

• gomitolo azzurro = caduta a spirale;
• arancio = orbita circolare (prima velocità cosmica);
• pallini verdi = orbita reale (leggermente ellittica);
• nera = orbita ellittica pronunciata;
• rossa = orbita parabolica (seconda velocità cosmica);
• verde = orbita iperbolica.

Conclusioni

Questo articolo ha provato a descrivere e simulare il moto della Terra attorno al Sole nella situazione reale ed in alcune ipotesi di diversa velocità al perielio. Si è visto che cambiamenti anche modesti della velocità produrrebbero modifiche notevoli dell'orbita. Che facilmente o sicuramente sarebbero incompatibili, con le condizioni di vita della nostra specie e di gran parte del regno animale. Come è stato messo in luce da molti è dunque un caso molto strano, particolare e davvero fortunato che si sia determinata per il nostro pianeta una situazione astronomica adatta allo sviluppo della vita biologica, almeno nella forma che conosciamo, vale a dire basata sulla chimica del carbonio e con la struttura cellulare a doppio filamento del DNA, comune a tutte le specie.
Questo ha autorizzato alcuni a formulare la (discutibile) ipotesi denominata Principio Antropico.
La semplice teoria della gravitazione universale, a partire da Newton, ha rappresentato il punto di svolta per lo sviluppo del pensiero scientifico e della sperimentazione, permettendo all'uomo di liberarsi dalle concezioni primitive e irrazionali sulla natura. Fino ad oggi è la base per calcolare il moto dei corpi celesti e per tutte le imprese nello spazio: satelliti artificiali (inclusa la Stazione Spaziale Internazionale), spedizioni lunari, invio di navette e rover su Marte, piani per la sua conquista.

Per ulteriori approfondimenti sulla gravitazione vedi anche qui