Da Pitagora a Fermat a Homer

In questo questo breve articolo vengono messe a confronto, con semplici esempi, discipline molto diverse come: la storia della matematica, la geometria, la teoria dei numeri, i controlli empirici, il calcolo numerico, l'ottimizzazione e i fumetti dei Simpson.

Introduzione: Pitagora e Kant

Il teorema della matematica più noto, appreso a scuola nel passato e dalle tre o quattro generazioni oggi viventi, è sicuramente il teorema di Pitagora.
La leggenda narra che Pitagora, camminando all'interno di un tempio osservasse le piastrelle identiche e quadrate all'interno delle quali erano tracciate le due diagonali.
Fu facile per il filosofo e matematico intuire che i quadrati costruiti sui due cateti misuravano ciascuno due mezze piastrelle e che il quadrato costruito sull'ipotenusa misurasse 4 mezze piastrelle, dunque: la somma delle aree dei quadrati costruite sui cateti è uguale all'area costruita sulla ipotenusa.

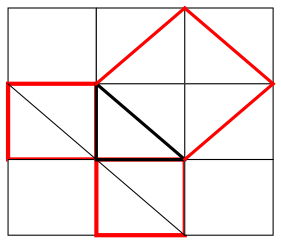
Naturalmente si tratta di un caso particolare relativo ai triangoli rettangoli isoscele (i lati dei cateti sono eguali), ma bastò a Pitagora per riflettere, generalizzare e formulare il suo teorema.
Al di la della leggenda, oggi sappiamo che molte terne pitagoriche "intere" erano già note ai Babilonesi secoli prima di Pitagora (vedi in Bibliografia il riferimento alla celebre tavoletta Plimpton 322).

In particolare i Babilonesi, come oggi tutti noi, conoscevano la più piccola terna pitagorica intera: 3, 4, 5. Infatti:

Semplificando al massimo il pensiero di Kant possiamo dire che i giudizi (le argomentazioni, le spiegazioni) umane siano di tre tipi:

• Giudizi analitici a priori. Analitici perché i risultati sono già compresi nelle premesse e a priori perché non necessitano della esperienza empirica. Ad esempio tutti i giudizi che scaturiscono dalla logica;
• Giudizi sintetici a posteriori. Sono sintetici perché i risultati non sono compresi nelle premesse e a posteriori perché derivano dalla esperienza empirica. Ad esempio tutti i giudizi che scaturiscono dalla scienza moderna;
• Giudizi sintetici a priori. Sono sintetici perché i risultati non sono compresi nelle premesse e a priori perché non necessitano della esperienza empirica. Di questo tipo sono, secondo Kant, i giudizi che scaturiscono dalla matematica.

In tempi recenti i coreani del Sud (vedi i DVD di Marcus du Sautoy citati tra i riferimenti) pare abbiano voluto spostare il teorema di Pitagora dalla famiglia 3) alla famiglia 2) di Kant: in pratica si sono impegnati a verificare empiricamente la validità del teorema.
Il teorema di Pitagora è fortemente imparentato con il concetto di distanza e con la disuguaglianza triangolare (la distanza più breve tra due punti è data dal segmento di retta che li congiunge - vedi wikipedia). Feynman, che amava molto la ricerca delle soluzioni semplici ai problemi, racconta come suo padre chiamasse l'ipotenusa: "scorciatoia".
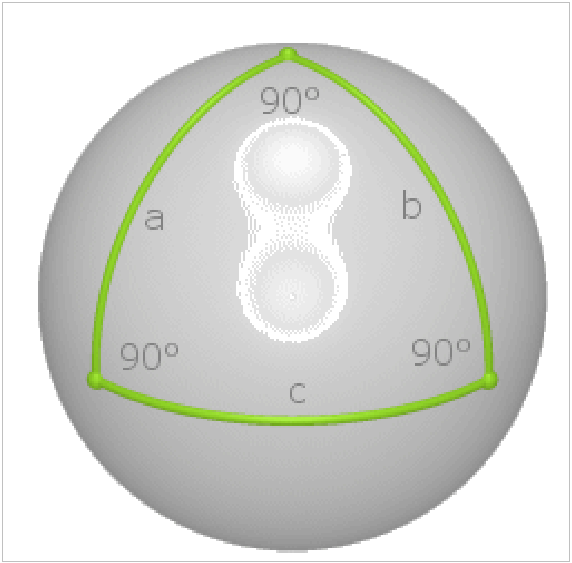
I Coreani, disponendo di sistemi laser di misura delle distanze estremamente precisi, hanno impiantato, in un campo di calcio, tre stazioni di misura disposte a triangolo rettangolo. I risultati sono stati perfetti, salvo qualche ennesima cifra decimale. I matematici giustificarono la insignificante differenza con trascurabili errori dei sistemi di misura, gli ingeneri hanno escluso che da questi potesse derivare la discrepanza. Quindi si è deciso di rifare le misurazioni più in grande, partendo da un punto a nord della Corea e da due isole in basso: i tre punti formavano un triangolo rettangolo gigantesco. Sistemi satellitari e raggi laser garantivano una precisissima misura dei due cateti e della ipotenusa. Questa volta la discrepanza fu molto più accentuata, dunque il teorema di Pitagora era stato falsificato dall'esperimento? Il fatto è che il teorema vale nel piano, ma non su una sfera o meglio su una specie di ellissoide schiacciato ai poli. Tenendo conto dell'alterazione dovuta alla curvatura terrestre i conti tornarono alla perfezione, anche nel caso del campo di calcio, dove l'effetto della curvatura era minimo.

La congettura di Fermat

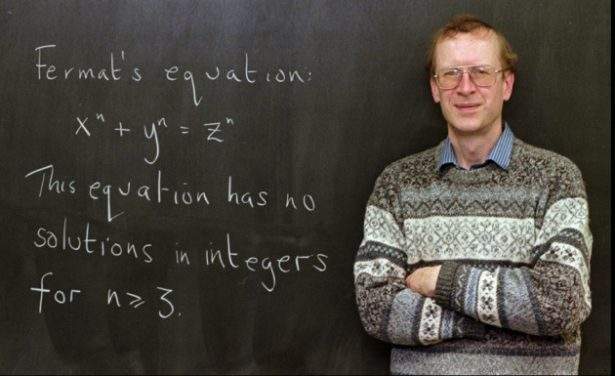
Fermat era un magistrato francese, ma anche dilettante (il !) appassionato di matematica. Celebri i suoi carteggi con Pascal con cui, tra l'altro, scrivendo del gioco d'azzardo, fondò la teoria delle probabilità.
Tra le passioni di Fermat c'era il matematico Diofanto vissuto tra III e IV secolo dopo Cristo ad Alessandria d'Egitto. Diofanto è celebre per aver studiato le equazioni a coefficienti interi che hanno per soluzione valori interi delle incognite.
Leggendo la Arithmetica di Diofanto, Fermat annotò al margine del volume:

«È impossibile dividere un cubo in altri due cubi, una quarta potenza o in generale una potenza qualsiasi in due potenze dello stesso valore maggiore del secondo. Dispongo di una meravigliosa dimostrazione di questo teorema che non può essere contenuta nel margine troppo stretto della pagina ».

In termini matematici la nota di Fermat significava che l'equazione:

Non può avere soluzioni, con X,Y,Z,n interi, se n è maggiore di 2 (se n=2 ricadiamo nell'ambito del teorema di Pitagora di cui molte soluzioni intere erano già note ai babilonesi). Questa congettura, poi nota come ultimo teorema di Fermat anche se teorema non era, colpì sia i matematici che i dilettanti, dell'epoca e dei tre secoli successivi, poiché, vista la semplicità dell'enunciato, in molti provarono, ma senza successo, a confermarla o a confutarla. Lo stesso Fermat dimostrò poi, con il metodo per assurdo denominato "discesa infinita" (vedi Wikipedia) la validità della sua congettura per il caso particolare di n=4. Storici, filosofi e matematici si accapigliarono a lungo per cercare di capire se Fermat avesse davvero trovato una soluzione generale al problema o se avesse voluto semplicemente burlarsi dei suoi contemporanei e dei posteri. Celebri matematici dimostrarono vera la congettura di Fermat per casi particolari di n

. Hilbert, all'inizio del 1900, indicò "La congettura di Fermat" come uno dei grandi problemi matematici aperti per il nuovo secolo. La congettura trovò conferma (se n > 2, non ci sono soluzioni) nel 1994 quando Andrew Wiles, dopo 7 anni di lavoro e dopo una dimostrazione errata del 1993, presento la complessa dimostrazione. Durante la presentazione pubblica, durata alcune ore, i dipartimenti di matematica di tutte le università del mondo entrarono in fibrillazione alla notizia: "Andrew Wiles sta dimostrando l'ultimo teorema di Fermat…". Nel 2016 l'accademia delle scienze norvegese conferì a Sir Andrew Wiles il premio Abel (il più prestigioso nell'ambito della matematica assieme alla medaglia Fields) per la sua splendida dimostrazione della congettura di Fermat. Era possibile che Fermat fosse arrivato alla dimostrazione di Wiles? Questo è da escludere perché la complessa matematica utilizzata da Wiles non era disponibile ai tempi di Fermat. Era possibile che Fermat avesse realmente trovato una più semplice dimostrazione della sua congettura? Questo è ritenuto oggi dai matematici estremamente improbabile, anche se, come vedremo nel seguito, i tentativi (anche divertenti) per trovare scorciatoie alla soluzione non sono mancati, pure in tempi recenti.

Le "quasi soluzioni" di Homer

Simon Singh, nel suo libro "L'ultimo teorema di Fermat" citato in bibliografia, fa un storia precisa, ma anche avvincente della congettura di Fermat e dei tentativi fatti nel corso dei secoli per dimostrarla o falsificarla. Sempre Singh, nel libro "La formula segreta dei Simpson" racconta un aspetto particolare delle strisce di Homer, modesto impiegato americano, ignorato più che vessato dal suo terribile capo Montgomery Burns capitalista e neoliberista. Homer è un colto, appassionato di matematica e non stupisce quindi che i suoi interessi si rivolgano anche alla congettura di Fermat.
Con grande soddisfazione mostra di aver falsificato la congettura con i seguenti valori:

Il suo foglio Excel, impostato con ben 7 decimali da conferma del successo!
Vediamo però cosa accade prendendo in considerazione i due termini della equazione e la loro differenza, residui, errori o scarti (slack). Dunque tra il primo e secondo termine della equazione di Homer esiste uno scarto dell'ordine di

tutt'altro che trascurabile!
Homer però, non si da per vinto e torna alla carica con una nuova soluzione della equazione, calcolata sempre con l'esponente

Purtroppo questa soluzione è forse peggiore della precedente infatti facendo i conti in Excel risulta.
Dunque questa volta lo scarto o errore è addirittura dell'ordine di

Come si può dare aiuto a Homer, partendo dall'esponente a lui caro (n=12), per cercare, se non un errore = 0 impossibile, almeno un errore con ordine di grandezza inferiore a quelli da lui trovati? Dal buon senso, confortato dal risolutore Excel, risulta che esiste una doppia infinità di soluzioni (se volete ovvie) che hanno un errore molto inferiore a quello registrato da Homer:

Estrapolando il caso ad esponenti diversi da 12 si può ipotizzare la seguente legge (potenze di 2) che indica la differenza (o errore) minima in funzione dell'esponente n nella equazione di Fermat.

Il risolutore, provato su molti di questi casi, sembra confermare la validità della legge, ma come sappiamo non basta. Einstein diceva: Nessuna ulteriore verifica sperimentale potrà confermare definitivamente la mia teoria, ma basterà un solo esempio contrario per renderla vana. In seguito, sul primato della falsificazione rispetto alla verifica, Popper in "Congetture e confutazioni" ha costruito la sua filosofia della scienza:

Minimizzazione dell' errore, residuo o differenza

Vediamo come si può impostare la congettura di Fermat con la programmazione matematica (ottimizzazione di una funzione) con l'obiettivo di trovare una soluzione che minimizzi la differenza tra i due termini della equazione diofantea. Sappiamo già, da quanto affermato da Fermat e dimostrato da Wiles, che tale differenza non potrà essere nulla. Il problema non è semplice, siamo infatti alle prese con numeri interi, potenze e valori assoluti, dunque si tratta di un problema di programmazione non lineare, vincolato e a numeri interi.
Dobbiamo in pratica calcolare la differenza tra i due termini dell'equazione in valore assoluto (e = errore), cercare di minimizzare questo valore, assicurandoci che l'esponente "n" sia maggiore di due, la terna di numeri sia maggiore di uno e che le quattro variabili del problema siano intere. In termini matematici ecco l'impostazione del problema:

Dunque, con buona pace di Homer, la soluzione che ha errore (differenza, residuo, ecc.) minimo sembra essere:

L'amico Hume (vedi in bibliografia due articoli sulla ottimizzazione) mi segnala che, con esponente n = 3, esistono almeno altre due terne (X,Y,Z) che hanno ABS(e) = 1. Invito i lettori curiosi ed interessati ad individuarle.
Dunque l'ipotesi precedentemente avanzata che l'errore sia eguale a

(nell'esempio ) deve essere rigettata? Sicuramente si, almeno in questa forma stretta.
Ad esempio per n = 5, l'errore dovrebbe essere , invece il risolutore fornisce la soluzione.
Possiamo però recuperare la congettura legata alle potenze di 2 come formula di maggiorazione dell'errore: per qualunque valore di n vale la relazione:

Dunque questa analisi numerica del problema conferma, come previsto ed inevitabile, la congettura di Fermat e la dimostrazione che ne ha dato Wiles, ma aggiunge qualcosa di più sulla entità della differenza errore (e). Poichè:

Si ha sempre, per qualunque valore di n maggiore di 2:

Conclusioni

Torniamo ai babilonesi e alle terne pitagoriche intere (n=2). Perché i babilonesi hanno esplorato queste terne in cui il perimetro dei triangoli rettangoli è piuttosto basso? Secondo alcuni per motivi molto pratici, come la misura dei campi, secondo altri forse per motivi didattici, per istruire i più giovani; certamente le due tesi non sono in contrapposizione tra loro.

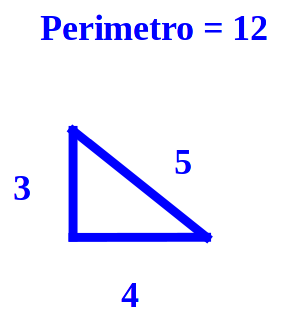
Noi, possiamo chiederci quante e quali sono le terne pitagoriche intere a perimetro più elevato? Ad intuito possiamo avanzare la seguente congettura:

"Le terne pitagoriche intere sono infinite, ma la loro densità, nel piano x-y, è decrescente al crescere del perimetro dei triangoli rettangoli".

Ripensando al triangolo rettangolo geografico con un perimetro di migliaia di kilometri costruito dai coreani possiamo chiederci: quale è la terna pitagorica intera di massimo perimetro calcolabile con il nostro computer/algoritmo/software?

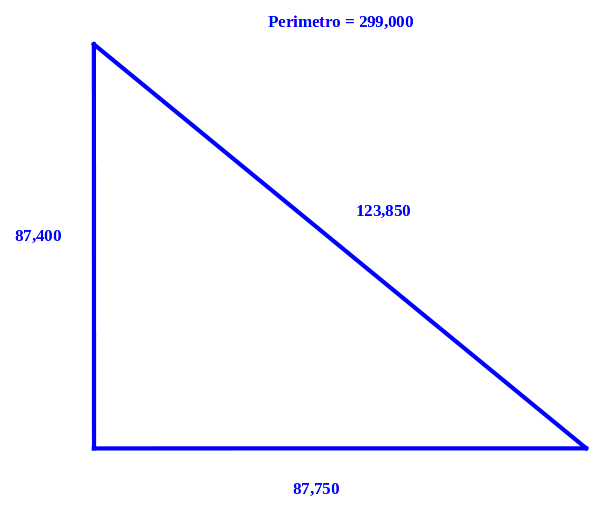
Il risolutore qui utilizzato trova come triangolo a perimetro massimo quello riportato sopra. Se gli si permette di cercare anche tra perimetri superiori (sono state fatte prove con perimetro massimo sino a 1,000,000) informa che non è in grado di trovare soluzioni (probabilmente nella elaborazione si genera qualche overflow). Si deve tener presente che quando si lavora con la programmazione matematica (indipendentemente quindi dal tipo di risolutore), se si cerca un massimo, è comunque necessario dare dei vincoli superiori entro cui effettuare la ricerca, in caso contrario infatti la regione ammissibile non sarebbe chiusa, ma illimitata rendendo impossibile a qualunque algoritmo ottimizzante di operare e convergere ad un risultato.

Non dovrebbe comunque essere difficile costruire algoritmi enumerativi (quindi non di ottimizzazione) in grado di generare triangoli rettangoli interi più grandi. Lasciamo anche questa ricerca ai lettori curiosi ed interessati. L'ultimo riferimento riportato (terne pitagoriche primitive e derivate) permette di accedere ad un programma che consente di enumerare tutte le terne, primitive e non che hanno cateti e ipotenusa inferiori a 5,000.

Riferimenti

• Il teorema di Pitagora al tempo dei babilonesi (I.N.A.F.);
• Terne pitagoriche (Wikipedia);
• Il teorema di Pitagora (Wikipedia);
• Disuguaglianza triangolare;
• Distanza euclidea (Wikipedia);
• Triangolazioni (Wikipedia);
• P. Odifreddi, "Pitagora, Euclide: la nascita del pensiero scientifico", Le Scienze DVD, Roma 2010;
• Equazione diofantea (Wikipedia);
• Pierre de Fermat (Wikipedia);
• Ultimo teorema di Fermat (Wikipedia);
• Discesa infinita (wikipedia);
• Andrew Wiles (Wikipedia);
• Simpson Comics (Wikipedia);
• Simon Singh, "L'ultimo teorema di Fermat", Rizzoli, Milano 1997;
• Simon Singh, "La formula segreta dei Simpson", Rizzoli, Milano 2014;
• Andrew Wiles, "La Teoria dei numeri", Le Scienze DVD, Roma 2010;
• Marcus du Sautoy, "Viaggio nella matematica", Corsera DVD, Milano 2016;
• L'ultimo teorema di Homer;
• Hume e Smith: Problemi, algoritmi e codici;
• Hume e Smith: Programmazione matematica;
• Terne Pitagoriche Primitive e Derivate (programma che le genera).