Rapporto aureo tra superfici

Sommario

Queste note descrivono la scoperta (ma è tale?) del tutto casuale del rapporto aureo tra alcune superfici legate in qualche modo al numero d'oro.

L'anno scorso ho pubblicato un libro sulla Trigonometria¹ e mi sono deciso ad apportare dei miglioramenti e delle piccolissime correzioni.

In particolare voglio aggiungere qualcosa sul rapporto aureo. Ho pensato quindi alla costruzione, da una figura semplice data, di un segmento che diviso per un segmento unitario dia il famoso numero d'oro.

[caption id="attachment_18856" align="alignleft" width="571"]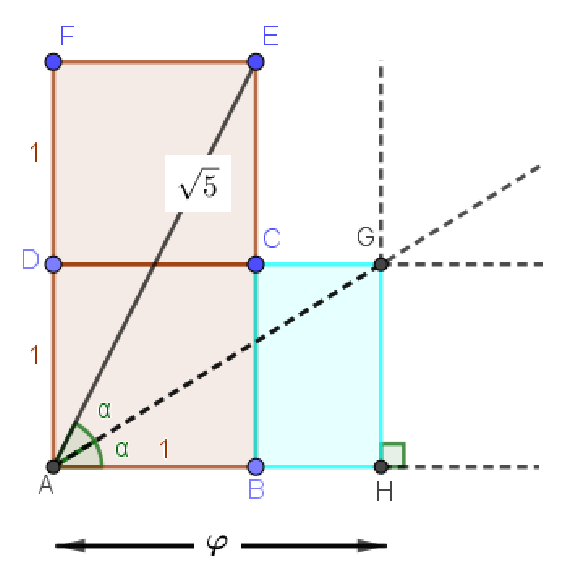 Figura 1: Costruzione segmento di misura

Partendo dal rettangolo

(figura 1) i cui lati misurano 2 e 1, si disegna la diagonale e la bisettrice dell'angolo che, per comodità, misura , in modo che ciascuna delle sue metà misuri . Il prolungamento del segmento (che divide a metà il rettangolo dato), dalla parte di interseca la bisettrice nel punto . Da si invia la perpendicolare al prolungamento, dalla parte di , del lato del rettangolo, ottenendo, per intersezione il punto . Il punto è tale che il rapporto , numero d'oro, numero irrazionale molto studiato non solo in matematica da oltre duemila anni.

Infatti dal triangolo

risulta:

( AH = HGcot alpha = cot alpha = frac{1 + cos 2alpha}{\sin 2alpha} = = frac{1+frac{1}{\sqrt{5}}}{frac{2}{\sqrt{5}}} = frac{1 + \sqrt{5}}{2} = phi )

dove le espressioni di (\sin 2alpha) e di (cos 2 alpha) sono dedotte dal triangolo

e rappresenta il rapporto aureo o numero d'oro, di cui una proprietà fondamentale è questa:

[ phi = 1 + frac{1}{phi} Leftrightarrow phi^2 - 1 = phi ]

[caption id="attachment_18855" align="alignleft" width="615"]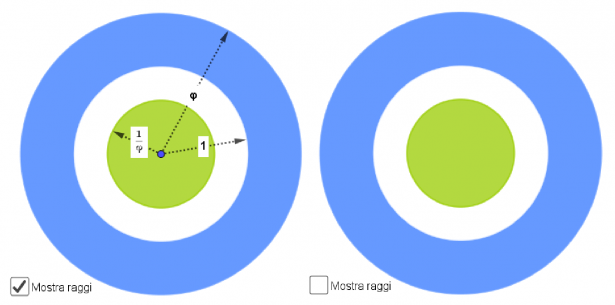 Figura 2: Tre superfici (corona circolare esterna, corona circolare centrale, cerchio centrale) in rapporto aureo

Dopo aver completato il disegno e il calcolo mostrato prima, ho cominciato a disegnare tre circonferenze concentriche con raggi rispettivi (in ordine decrescente):

e come nella figura 2.

Calcolo le aree di alcuni cerchi e corone circolari (non tutte mostrate in figura 2):

• [math]A_0[/math]
  (cerchio di raggio
  [math]\phi[/math]
  ):
  [math]\pi \phi^2[/math]
• [math]A_1[/math]
  (corona circolare di raggi
  [math]\phi[/math]
  e
  [math]1[/math]
  ):
  [math]\pi \phi^2 - \pi \cdot 1^2 = \pi (\phi^2-1) = \pi \phi[/math]
• [math]A_2[/math]
  (cerchio di raggio
  [math]1[/math]
  ):
  [math]\pi[/math]
• [math]A_3[/math]
  (corona circolare di raggi
  [math]1[/math]
  e (1/phi)):
  [math]\pi (1^2 - 1/\phi^2)=\pi (\phi^2-1)/\phi^2 = \pi \phi/\phi^2 = \pi/\phi[/math]
• [math]A_4[/math]
  (cerchio di raggio (1/phi)):
  [math]\pi/\phi^2[/math]
• [math]A_5[/math]
  (corona circolare di raggi (1/phi) e (1/phi^2)):
  [math]\pi (1/\phi^2-1/\phi^4)=\pi((\phi^2-1)/\phi^4)=\pi \phi/\phi^4=\pi/\phi^3[/math]
• [math]A_6[/math]
  (cerchio di raggio (1/phi^2)):
  [math]\pi/\phi^4[/math]
• [math]...[/math]
• [math]A_k = \pi/\phi^{k-2}=\pi \phi^{2-k}[/math]

Calcolo i rapporti tra una e la sua successiva e trovo sempre il valore costante :

[ frac{A_0}{A_1} = frac{A_1}{A_2} = frac{A_2}{A_3} = ldots = frac{A_{k-1}}{A_k} = phi ]

cosa straconosciuta e molto trattata nei manuali e in innumerevoli articoli per le dimensioni lineari e non per le superfici. Per questo la cosa mi ha incuriosito non poco ed ho esitato molto a scrivere queste brevi note, controllando a destra e a manca se non fosse stato scritto qualcosa in proposito. Ma non ho trovato niente.

In effetti la successione precedente definisce due successioni separate:

1. (con
   [math]k[/math]
   pari) cerchi
   [math]C_k[/math]
   aventi raggi
   [math]r_k = \phi^{k-1}[/math]
   e area
   [math]A_k = \pi \phi^{2-k}[/math]
2. (con
   [math]k[/math]
   dispari) corone circolari
   [math]c_s = A_((k+1)/2)[/math]
   aventi raggi
   [math]r_k = \phi^{k-1}[/math]
   e
   [math]r_(k+1) = \phi^{k-2}[/math]
   con area
   [math]c_s = \pi \phi^{1-s}[/math]

Risulta (come ci si aspetta):

[ frac{C_h}{C_{h+1}} = frac{piphi^{2-k}}{piphi^{2-(k+2)}} = phi^2 ,,,, mbox{ e } ,,,, frac{c_h}{c_{h+1}} = frac{pi phi^{1-k}}{pi phi^{1-(k+2)}} = phi^2 ]

Qualcosa di interessante si trova pure considerando dei dischetti (cilindri, anche opportunamente bucati o trasformati in anelli) di altezza costante e raggi successivi (phi, 1, 1/phi, 1/phi^2, ldots ) lascio il divertimento al lettore ormai (spero) incuriosito!

Note

1. Raffaele Santoro, Trigonometria - Per neo peofessori di Matematica, studenti e appassionati, RSEdizioni, 2017, venduto da Amazon. ↑