Un personaggio importante nella storia della matematica è la governante di casa Riemann, che si abbandonò a una pulizia troppo approfondita nell'appartamento dello studioso dopo la morte di questi avvenuta a soli trentanove anni il 20 luglio 1866. Sette anni prima, Riemann aveva congetturato che per conoscere la distribuzione dei numeri primi occorresse esaminare gli zeri della funzione Zeta introdotta da Eulero
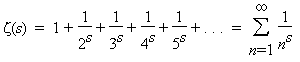
previa sostituzione della variabile “s” con la variabile complessa “x+iy”.
Potete facilmente trovare l'articolo di Riemann sul web, sia nella traduzione inglese sia nella forma originale (“Über die Anzahl der Primzahlen unter einer gegebenen Größe”, Sul numero di primi inferiori a una determinata grandezza).Bernhard Riemann era rigorosissimo e poco incline a divulgare risultati che non fossero abbondantemente verificabili. Infatti pubblicò pochissimo. Proprio per questa ragione, e anche a giudicare dai reperti che i biografi riuscirono a procurarsi negli anni presso la pur recalcitrante vedova, è lecito supporre che in casa, prima che la governante agisse quel giorno di luglio, si trovassero appunti di inestimabile valore. Stiamo parlando di uno dei più grandi matematici di ogni tempo, che diede contributi originali e fondanti alla geometria differenziale, alla geometria algebrica, alla topologia, all'analisi reale, molti dei quali richiedettero due generazioni di studiosi per essere compresi.
Solo una volta Riemann aveva fatto una concessione, proprio in quella comunicazione inviata nel 1859 all'Accademia Prussiana delle Scienze di Berlino intorno a un argomento del quale non si era mai occupato e sul quale non tornerà: la teoria dei numeri. A pagina 4 scrisse: «[..] È molto probabile che le [...] radici siano reali. Certo, uno qui vorrebbe una dimostrazione. Ma ne ho temporaneamente abbandonato la ricerca dopo alcuni tentativi infruttuosi. E del resto essa non è necessaria per gli scopi della trattazione che segue».
Secondo Riemann, che lo affermò “a naso” e senza dimostrarlo, la funzione Zeta si annulla solo per valori di x=1/2 (ci sono poi “zeri banali” per valori negativi di x, ma questi non sono significativi). Se si provasse vera tale ipotesi, oltre a disporre del metodo migliore per predire le posizioni dei numeri primi sulla retta reale, si verificherebbe tutta una messe di conseguenze per l'analisi matematica, la crittografia e una varietà di altri contesti.
La congettura di Riemann è assurta nel corso dei decenni al rango di ipotesi, grazie a molti indizi intervenuti e al fatto che non sono mai stati ravvisati zeri della funzione Zeta al di fuori della retta x=1/2. Per esempio, nel 1915 Hardy ha dimostrato che lungo quella linea critica stanno infiniti zeri di Zeta. Nel 1986 si è mostrato che i primi 1.500.000.001 zeri non banali sono in effetti lungo quella retta. Nel 1989 Conrey ha provato che più del 40% degli zeri sono sempre lì. Dal 2001 al 2005 Sebastian Wedeniwski ha fatto girare la ZetaGrid, ossia undicimila workstations che producevano fino a 7 TeraFLOPS e calcolavano un miliardo di zeri al giorno, individuando i primi novecento miliardi di zeri, tutti sulla linea critica. Credo che oggi si sia arrivati ai primi 10mila miliardi di zeri.
Insomma, un'ipotesi tanto fondata che, dopo Alan Turing, quasi a nessuno viene più in mente di provarsi a dimostrarla falsa! Sono ormai molti i risultati matematici ottenuti assumendo come vera l'ipotesi di Riemann, ed esiste una fiorente letteratura su quelle che sarebbero le conseguenze e le implicazioni del teorema.
Da quando fu formulata, e soprattutto in seguito alla sua comparsa tra i celebri Problemi del Millennio di Hilbert nel 1900, l'ipotesi di Riemann è una delle sfide più difficili e ambìte della matematica. Vi ci sono cimentati pensatori grandissimi, tra i quali l'italiano Enrico Bombieri, secondo cui si tratterebbe del più importante problema irrisolto della matematica pura. La storia dei tentativi fatti per dimostrarla (solo su arXiv.org, in febbraio 2011, se ne trovavano un paio di dozzine) è lunga più di un secolo e costellata anche di episodi coloriti.
Uno dei più buffi e intriganti è quello riguardante Louis de Branges, americano nato a Parigi nel 1932 che si distinse nel 1984 per aver provato un altro problema assai difficile e vecchio di cinquant'anni, la congettura di Bieberbach, la quale infatti va nota adesso come teorema di de Branges. 
Già allora de Branges aveva faticato a far accettare la propria dimostrazione, perché vent'anni prima aveva fatto ammattire tutti annunciando una serie di risultati strampalati, con dimostrazioni sbagliate la cui fallacia era proporzionale alla grandezza delle sfide che si era scelto.
Oggi lo scetticismo dei colleghi perdura: de Branges porta con sé la “maledizione” delle sue dissolutezze intellettuali degli anni Sessanta e forse anche un po' di invidia per i risultati importanti che ha in ogni caso conseguito. Inoltre utilizza strumenti di analisi matematica così astrusi e personali che in pratica solo lui e qualche (raro) allievo ne hanno familiarità, il che non contribuisce ad accrescere la platea degli studiosi interessati alla sua produzione scientifica. Il risultato è che il suo lavoro sull'ipotesi di Riemann è parecchio snobbato, nonostante si tratti del solo matematico insigne che abbia mai annunciato di averla dimostrata!
D'altra parte, l'atteggiamento di de Branges è quantomeno curioso. Egli sostiene di aver dimostrato l'ipotesi e lo fa in due file Pdf che da una decina d'anni appaiono e scompaiono in successive versioni sul sito web della Purdue University, dove è professore. Uno consta, nella versione attuale (che risale al settembre 2009), di 71 pagine e contiene la dimostrazione vera e propria. L'altro, 43 pagine risalenti mentre scrivo all'aprile 2010, fornisce il contesto.
Il documento più interessante per i matematici è il primo, “Riemann Zeta Functions”: ma mi risulta che quasi nessuno se ne occupi. Il più interessante per me, invece, è il secondo, “Apology for the proof of the Riemann hypothesis”, ossia “Chiedo venia per aver dimostrato l'ipotesi di Riemann” (o, secondo alcuni ma a mio parere meno credibilmente, “Apologia della dimostrazione dell'ipotesi di Riemann”). In questo scritto de Branges sembra voler fornire una spiegazione del perché la sua dimostrazione, che se vera sarebbe un risultato storico, non venga compresa dai colleghi.
«Scrivere bene di matematica è difficile perché il lettore sa o troppo o troppo poco» dice de Branges in apertura, e fa seguire 20 pagine piuttosto pedanti di storia della matematica che servono a offrire un contesto agli strumenti di analisi utilizzati per la dimostrazione. Poi aggiunge che l'impresa è stata «resa possibile da eventi che a prima vista sembrano non avere nulla a che fare con la matematica. Persone eccezionali e circostanze eccezionali hanno preparato la dimostrazione dell'ipotesi di Riemann». Ed ecco una quindicina di pagine di storia della famiglia dell'autore, con albero genealogico dettagliatamente narrato sino al 1199, fotografie degli zii e aneddoti curiosi. Apprendiamo, fra l'altro, che il nostro si appassionò alla fatale sfida di Riemann quando era matricola all'Università.
Insomma, un bel tipo. Si è tentati di non prenderlo sul serio, visti i precedenti e l'eterodossia con cui propone la sua presunta clamorosa scoperta su una specie di blog e senza averla mai pubblicata su un journal o almeno su arXiv, alla Perelman. In più, i suoi modi possono essere ritenuti, come io credo siano, sprezzanti da parte dei colleghi.
Però, aspettate un attimo. Cosa ho detto? Prendere sul serio? Ortodossia? Furono presi sul serio, inizialmente e in alcuni casi per tutta la vita, Galois, Grassmann, Cantor, Ramanujan? E non era forse eterodosso Gödel, che praticamente morì di fame a Princeton perché non sapeva badare a se stesso? E Grisha Perelman, che non va a ritirare né la Fields Medal né il milione di dollari del Clay Millennium Price e rinuncia senza nemmeno rispondere a cattedre dorate nella Ivy League?
La verità è che non possiamo “prendere sul serio” un matematico, la grandezza della cui arte sta, prima ancora che nel rigore, nella bellezza, nella purezza eterea e nell'audacia delle sfide. Più un matematico è grande, meno possiamo prenderlo sul serio, perché i canoni ordinari della professionalità non si applicano. E i matematici lo sanno. Ecco perché quel blog di de Branges leva il sonno anche a quelli che fingono di non farci caso.
Paolo Magrassi
