Aritmetica indecidibile o incompleta? Terremoto nei fondamenti della matematica [Kurt Goedel]

"... si potrebbe quindi congetturare che questi assiomi e regole d'inferenza siano sufficienti a decidere ogni questione matematica che possa essere formalmente espressa in questi sistemi (Principia Mathematica di Russell, teoria dei sistemi nell'assiomatizzazione di Zermelo o Von Neumann). Verrà mostrato ... che non è così, che al contrario esistono nei due sistemi menzionati problemi relativamente semplici della teoria dei numeri che non possono essere decisi sulla base degli assiomi"

Sulle proposizioni formalmente indecidibili dei 'Principia Mathematica' e di sistemi affini (Kurt Goedel 1906 -1978).

"la soluzione di certi problemi aritmetici richiede l'uso di assunzioni che essenzialmente trascendono l'aritmetica, cioè il dominio di evidenza elementare indiscutibile che può essere meglio confrontato con la percezione sensoriale". "Grazie al lavoro di A.M. Turing può ora esser data una definizione precisa e indiscutibilmente adeguata del concetto di sistema formale, l'esistenza di proposizioni aritmetiche indecidibili e la non dimostrabilità della coerenza di un sistema all'interno del sistema stesso possono ora essere dimostrate rigorosamente per ogni sistema formale coerente che contenga un certo frammento di teoria finitaria dei numeri".

"... D'altra parte, sulla base di quello che è stato dimostrato finora, rimane possibile che possa esistere (e anche essere empiricamente scoperta) una macchina per dimostrare teoremi che di fatto è equivalente all'intuizione matematica [della mente umana], ma che non può essere dimostrata essere tale e nemmeno che fornisce solo teoremi corretti dell'aritmetica finitaria." (Appunti vari)

La scoperta di Goedel, che nessun sistema di assiomi coerente può essere completo per aree della matematica come la teoria dei numeri e quella degli insiemi rende impossibile il programma di Hilbert di fondare l'intera matematica su un numero finito di assiomi e dedurre poi da essi tutti i teoremi necessari. Lo stesso principio del terzo escluso viene ad essere messo in discussione perchè accanto a proposizioni 'vere' e proposizioni 'false' potranno trovarsi proposizioni "indecidibili" (almeno nell'ambito del sistema di assiomi definito).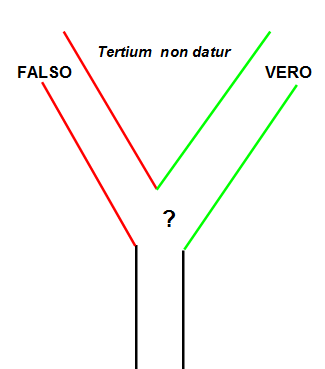

Ad esempio, il primo problema di Hilbert 'ipotesi del continuo' riproposto nel celebre convegno di matematica svoltosi all'inizio del 1900, che chiedeva di confermare la congettura: 'l'insieme dei numeri reali ha una infinità di ordine immediatamente superiore a quella dei numeri interi', è stato dimostrato essere "indecidibile" nel 1963 da Paul Cohen. Analogamente Il secondo problema di Hilbert, che chiedeva se fosse possibile dimostrare che gli assiomi dell'aritmetica sono compatibili, ossia che partendo da essi e procedendo attraverso un numero finito di passaggi logici non si può mai giungere a risultati contraddittori, è stato dimostrato dallo stesso Godel essere "indecidibile" nel suo celebre articolo del 1931.

Scrive Piergiorgio Odifreddi (Le Menzogne di Ulisse: L'avventura della logica da Parmenide ad Amartya Sen, Longanesi 2004): "Una delle conseguenze filosofiche dei teoremi di Goedel fu dunque la dimostrazione definitiva che il sogno logicista di Frege e Russell era irrealizzabile e che invece avevano ragione Kant e i suoi seguaci da Poincaré a Brouwer: l'aritmetica non è analitica, ma sintetica a priori. Le discussioni finiscono quì. Almeno per noi cioè, perché né Russell né Wittgenstein capirono l'antifona e, meno che mai, il salmo. Il primo credette per tutta la vita che Goedel avesse dimostrato che l'Aritmetica era inconsistente e il secondo si immaginò che ci fosse qualcosa di sbagliato in tutta la faccenda, perché non si poteva dimostrare che qualcosa non era dimostrabile". "...Nel 1948 Alfred Tarski dimostrò ... che la teoria dei numeri reali è completa e decidibile: l'esatto contrario cioè della teoria dei numeri interi (aritmetica). E la stessa cosa (cioè la completezza) vale, come ci si può aspettare dal modello di Hilbert, anche per la geometria ... Ancora una volta Poincaré e Brouwer avevano visto giusto nel sospettare che aritmetica e geometria fossero teorie sostanzialmente irriducibili l'una all'altra, e di natura completamente differente ...".

Nella matematica applicata, in particolare nella rappresentazione dei problemi mediante modelli, più che la decidibilità o indecidibilità teorica interessa la complessità computazionale degli algoritmi risolutivi. Esistono infatti problemi che pur essendo decidibili non dispongono di algoritmi che possano risolverli in tempi di calcolo ragionevoli neanche utilizzando i supercomputer più veloci: si dice che questi algoritmi hanno una complessità esponenziale (cioè il tempo di calcolo cresce esponenzialmente con la dimensione del problema). Per altri problemi decidibili sono invece conosciuti algoritmi polinomiali (cioè il tempo di calcolo cresce polinomialmente con la dimensione del problema) che ne consentono la risoluzione in tempi ragionevoli per qualunque computer adeguato, si parla allora di problemi trattabili.

Goedel era convinto dell'irriducibilità della mente al cervello. Il cervello secondo lui funziona essenzialmente come una macchina di Turing, ma il cervello è un calcolatore connesso a uno spirito, anche se lo spirito probabilmente non può sussistere senza il corpo; la sua convinzione è che gli stati possibili della mente siano infiniti (a differenza di quelli del cervello che sono finiti probabilmente a causa del numero finito di neuroni). Dunque per Goedel è molto probabile che il cervello funzioni come un computer, ma la mente e la cognizione non può essere ridotta a un processo del solo cervello al contrario della digestione che è invece riducibile a un processo del solo stomaco.

Nelle organizzazioni la situazione del problem solving (prevalenza di problemi poco strutturati rispetto a quelli ben strutturati della logica e della matematica) è assai differente, ma utili insegnamenti possono essere tratti dai risultati di Goedel anche se questi possono valere solo come stimoli per generare idee; è comunque necessario chiarire che le analogie/traduzioni tra discipline diverse (nello specifico dai problemi della matematica a quelli delle organizzazioni) sono sempre solo suggestioni e/o spunti di riflessione e non devono essere presi alla lettera.

Nelle organizzazioni, a fronte di problemi che richiedono decisioni, esistono i limiti della mancanza di informazioni e della incertezza (rischio) insita negli eventi. Questa situazione rende molti problemi difficilmente decidibili all'interno degli schemi (gli assiomi?) consolidati. Conseguentemente un primo suggerimento è quello di considerare punti di vista e prospettive diverse: anche i primi due problemi di Hilbert potrebbero forse essere risolti partendo da assiomi diversi? Una seconda considerazione riguarda la indecidibilità che non può essere accettata come soluzione alle problematiche di sopravvivenza delle organizzazioni. Non prendere posizione, non decidere riguardo ad un problema vitale di una organizzazione non significa solo riconoscere uno status, "indecidibile" , alla situazione problematica, ma vuol dire far si che la decisione sia presa automaticamente (e non si sa come!) dagli eventi. Significa in altre parole abbandonarsi alla gestione per emergenze continue.