_stan
di _stan
(320 punti)
23' di lettura
La teoria dei giochi viene fatta risalire ad un celebre carteggio del 1654 tra Blaise Pascal e Pierre de Fermat, un filosofo e un magistrato entrambi appassionati di matematica.

Ai due viene anche attribuito il fondamento moderno del calcolo delle probabilità. Effettivamente, tra i molti problemi che si posero vi era quello di stabilire come ripartire le poste, qualora un gioco d'azzardo ripetuto fosse interrotto prima del termine.
Nel 1838 l'economista Cournot studiò le condizioni di equilibrio di un duopolio cioè un mercato dominato da due aziende concorrenti che scelgano di attuare le proprie strategie per accrescere le quote di mercato e i rispettivi profitti.
Nel 1920 il matematico Emile Borel usò per primo la dizione "teoria dei giochi" riferendosi principalmente a giochi a due persone e a somma zero.

Sempre in quegli anni, degli stessi problemi si occupò anche il logico e matematico Ernst Zermelo.
La svolta per la soluzione dei giochi a due persone a somma zero avvenne nel 1928 quando Von Neumann, matematico ungherese naturalizzato americano, formulò il celebre teorema del Mini-Max che stabiliva, per questo tipo di giochi, l'esistenza, in ogni caso, di strategie pure o miste di equilibrio; le seconde vengono calcolate risolvendo un opportuno sistema di equazioni lineari. Nelle sue dimostrazioni Von Neumann si era servito del teorema del punto fisso formulato da Luitzen Brouwer nel 1910.
Nella sua tesi di laurea il matematico George Dantzig aveva descritto l'algoritmo del Simplesso per la soluzione dei problemi di programmazione lineare. Uno dei maggiori successi tra gli algoritmi di programmazione matematica; esso è infatti ancora oggi incluso nei Risolutori di software popolari come Excel. Nel 1948 Dantzig incontrò Von Neumann e, racconta, che da quell'incontro, sentendo descrivere il teorema del Mini-Max, si ispirò per la teoria della dualità in programmazione lineare. Per quanto riguarda il presente articolo ci si potrebbe fermare qui nel riportare i cenni storici, citiamo però ugualmente per completezza i principali sviluppi seguenti.
Nel 1944 Von Neumann scrisse assieme all'economista Oscar Morgenstern il testo fondante "Theory of Games and Economic Behavior". Il matematico John Nash racconta di aver presentato a Von Neumann nel 1950 la sua dimostrazione dei punti di equilibrio, che portano il suo nome (una generalizzazione del teorema del Mini-Max, per i giochi a due persone, non cooperativi e a somma non zero). Von Neumann dando una occhiata al lavoro disse: "sicuramente per la dimostrazione avrai usato il teorema del punto fisso di Kakutani del 1941"; così era. In quegli anni questo importante teorema matematico fu utilizzato anche da K.Arrow e G. Debreu in economia per lo sviluppo della teoria dell'equilibrio generale dei mercati.
Sempre negli anni 50 Flood e Dresher inventarono il seminale "dilemma del prigioniero" in cui si mostra che, nell' esempio, l'equilibrio di Nash non è Pareto-Ottimale in quanto dominato dalla soluzione in cui i due prigionieri collaborano.
Da ricordare poi, per i giochi cooperativi, i lavori di Shapley del 1953 e di Aumann del 1974 ed infine il lavoro di Robert Axelrod "The evolution of competition" del 1984 che, con simulazioni su computer di giochi ripetuti, dimostra che la strategia vincente, nelle situazioni tipo dilemma del prigioniero, è quella proposta da A. Rapaport: "tit for tat", ovvero: "pan per focaccia", ovvero: "occhio per occhio, dente per dente".
Anche se apparentemente non ha molte applicazioni la teoria dei giochi viene oggi utilizzata oltre che nelle applicazioni militari anche in economia, finanza, management, pianificazione strategica/tattica, scienze sociali, biologia, medicina.
Ecco infine un po' di concetti e di tassonomia relativi alla teoria dei giochi:

  • A due o più persone;
  • Non cooperativi o cooperativi (sono possibili accordi tra i partecipanti);
  • A somma non zero o zero (quello che vince uno lo perde l'altro);
  • A giocata singola o iterata (si usa molto la simulazione su computer);
  • Strategie pure: definite e determinabili per entrambi i giocatori;
  • Punti di Sella: strategie pure di equilibrio nei giochi a somma zero;
  • Strategie miste: probabilistiche, frequenze relative nei giochi iterati;
  • Strategie dominate: peggiori di un'altra per qualunque scelta dell'avversario;
  • Strategie non dominate, chiamate anche Pareto Ottimali;
  • Equilibri Mini-Max di Von Neumann nei giochi a somma zero;
  • Equilibri di Nash: strategie di equilibrio nei giochi non a somma zero.

Pattugliatori e Incursori

In una situazione di conflitto le nostre forze, nel seguito chiamate "amiche" sono impegnate a pattugliare un ampio tratto di mare per intercettare eventuali incursori delle forze "nemiche".
I tratti di mare interessati sono schematizzati con un rettangolo che prevede due linee di pattugliamento delle forze amiche. Si può, ad esempio volere che la linea più avanzata sia ancora coperta dalla nostra protezione aerea e che l'altra sia in posizione tale da dare il tempo, quando necessario, alle forze amiche di intervenire ed ingaggiare l'unità nemica avversaria. Naturalmente la probabilità di scoperta di eventuali incursori dipenderà, oltre che dalle caratteristiche del nostro sistema di scoperta e dalla natura del tratto di costa da difendere anche dalle strategie di pattugliamento attuate. Dividiamo il tratto di mare in quattro settori: A.B,C,D. Gli incursori avranno a disposizione quattro strategie possibili:
  • Entrare da A ed uscire da C;
  • Entrare da A ed uscire da D;
  • Entrare da B ed uscire da C;
  • Entrare da B ed uscire da D.
Supponiamo che le forze amiche abbiano a disposizione le seguenti quattro strategie di pattugliamento sulle due linee:
  • Pattugliare prevalentemente in A e C;
  • Pattugliare prevalentemente in A e D;
  • Pattugliare prevalentemente in B e C;
  • Pattugliare prevalentemente in B e D.

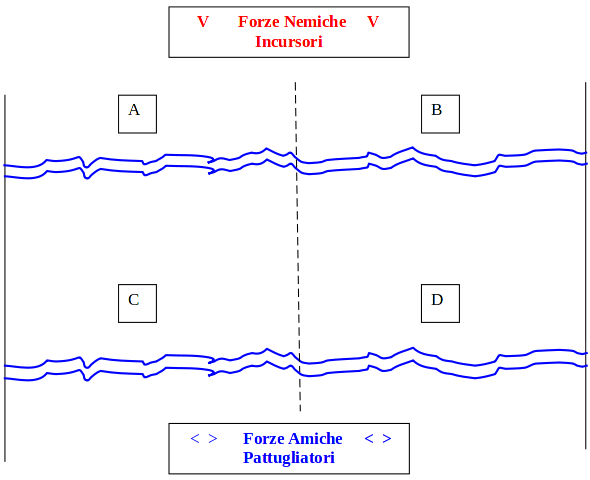
Supponiamo, ad esempio, che pattugliare prevalentemente in A significhi che le forze pattuglianti trascorrano lo 0.75 del tempo nel quadrante A e solo lo 0,25 del tempo nel quadrante B. Analogamente pattugliare prevalentemente in C significa trascorre lo 0.75 del tempo in C e solo lo 0.25 in D.
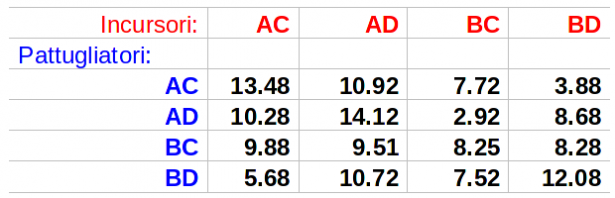
Con certe ipotesi sulla natura del nostro sistema radar, sulle caratteristiche (velocità, guerra elettronica, ecc.) degli incursori possiamo calcolare che se noi decidiamo di pattugliare prevalentemente in A e C e il nemico di entrare in A ed uscire da C la nostra probabilità di intercettarlo è pari a 13.48/25 = 53.92%. Analogamente possiamo calcolare le probabilità di intercettazione per tutte le 4*4 = 16 combinazioni di strategie possibili tra noi e il nemico. La risultante matrice 4*4 può essere interpretata come la matrice di un gioco a due persone e a somma zero, in quanto lo avvistamento è anche nostra vincita e perdita del nemico.
Nel seguito, per semplicità, abbiamo riportato la matrice del gioco a meno della costante moltiplicativa K = 1/25 in quanto essa non altera le caratteristiche del gioco.

Strategie pure e punti di sella

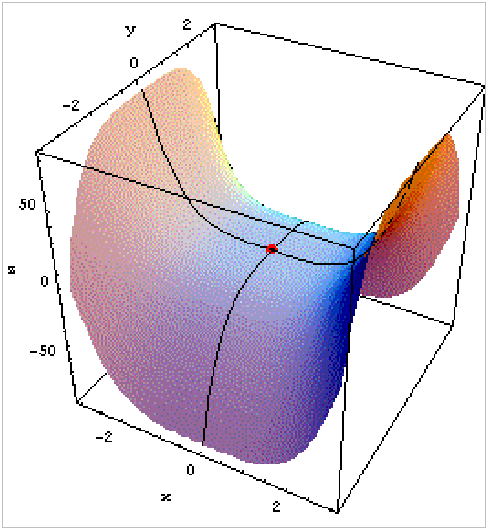
Strategia pura significa che entrambi i giocatori, ognuno non a conoscenza delle decisioni dell'altro, scelgano in modo univoco e deterministico una strategia. Abbiamo visto che, nel nostro caso, se entrambi i giocatori scelgono la strategia AC il risultato del gioco è 13.48. Cerchiamo ora di immaginare geometricamente cosa significa "Punto di Sella". Pensate ad un cavallo sellato; pensate poi ad un ipotetico piano longitudinale che lo sezioni dal muso alla coda. Su quel piano la sezione della sella sarà una specie di parabola con il vertice nel suo punto di minimo. Pensate ora ad un piano trasversale, ortogonale al precedente che sulla sella separi la testa dalla coda del cavallo. Su questo piano la sezione della sella sarà una specie di parabola rovesciata con il vertice nel suo punto di massimo. Il vertice, punto di minimo della prima parabola, coincide con il vertice, punto di massimo della seconda. Ebbene questa può essere una visione intuitiva dei punti di sella e del teorema del Mini-Max di Von Neumann.

Torniamo al nostro gioco e alla teoria razionale delle decisioni. I Pattugliatori sanno che giocano contro un nemico intelligente, che dunque li porterà alla soluzione peggiore per qualunque strategia essi scelgano, cioè al minimo di riga:

AC >> 3.88
AD >> 2.92
BC >> 8.25
BD >> 5.68

Analogamente gli Incursori sanno che giocano contro un nemico intelligente, che dunque li porterà alla soluzione peggiore per qualunque strategia essi scelgano, cioè al massimo di colonna:

AC >> 13.48
AD >> 14.12
BC >> 8.25
BD >> 12.08

Dunque è possibile completare come riportato sotto la matrice del gioco. In essa si vede chiaramente che nessuno dei due giocatori ha interesse, spostandosi unilateralmente, a cambiare la strategia di Sella (BC, BC, 8.25).
Un aspetto interessante, perché porta alla semplificazione della matrice, è che gli incursori possono eliminare la loro strategia AD in quanto essa risulta dominata dalla strategia BC. Basta confrontare i valori delle due colonne per concludere che AD ha valori sistematicamente più alti (dunque peggiori per il nemico) dei corrispondenti valori di BC.
Questa strategia non è Pareto-Ottimale mentre tutte le altre, sia degli incursori che dei pattugliatori lo sono e pertanto non possono essere eliminate dalla analisi del gioco.

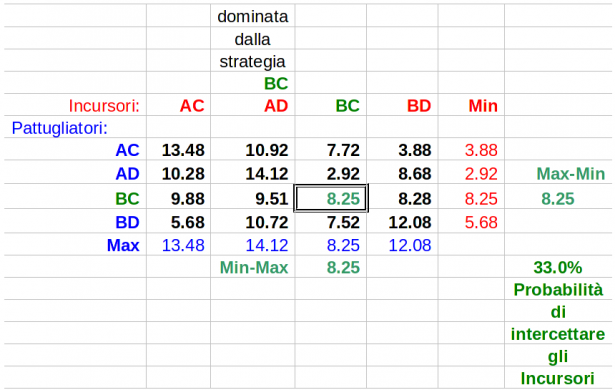
In conclusione Pattugliatori (BC) - Incursori (BC) sono le strategie pure di equilibrio del gioco; ad esse corrisponde il Valore 8.25 che rappresenta sia il Massimo dei Minimi delle righe che il Minimo dei Massimi delle colonne.

Strategie miste di equilibrio e teorema del Mini-Max di Von Neumann

Nel paragrafo precedente abbiamo visto che, nel caso di esistenza delle strategie pure di equilibrio di un gioco, il teorema di Von Neumann sia di interpretazione molto semplice:
Massimo dei Minimi di riga = Minimo dei Massimi di colonna = Valore del gioco.
Nel caso di non esistenza di strategie pure, il teorema afferma che esistono comunque delle strategie miste di equilibrio che debbono essere giocate con determinate e calcolabili probabilità assieme al Valore del gioco. Da esse nessuno dei due giocatori ha interesse a discostarsi. Illustriamo quanto scritto con un esempio. Consideriamo una situazione numerica leggermente diversa dalla precedente che, sempre a meno della costante moltiplicativa 1/25, è riportata sotto. Per prima cosa è da osservare che in questa nuova matrice la strategia AD degli incursori non è più dominata dalla strategia BC. Dunque essa deve essere presa in considerazione a tutti gli effetti.

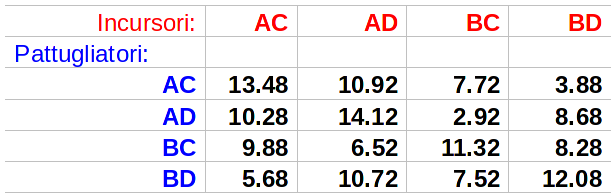
Cerchiamo ora eventuali strategie pure di equilibrio. A questo scopo è necessario, innanzi tutto calcolare i minimi di riga:

AC >> 3.88
AD >> 2.92
BC >> 6.52
BD >> 5.68

E i massimi di colonna:

AC >> 13.48
AD >> 14.12
BC >> 11.32
BD >> 12.08

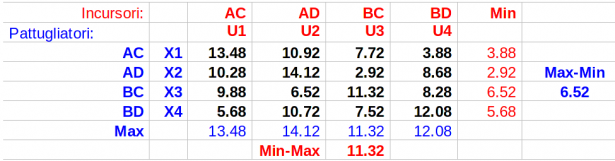
Come si può osservare il Massimo dei Minimi di riga non coincide con il Minimo dei Massimi di colonna. Possiamo dunque affermare che non esistono strategie pure di equilibrio e che non vi è un punto di Sella. L'unica cosa che si può affermare, per il Valore del gioco (V), è che valgono le relazioni:

6.52

Il teorema del Mini-Max di Von Neumann ci dice però che in ogni caso, se non esistono strategie pure di equilibrio, ne esistono di miste che debbono essere attuate con probabilità P che, sia sulle righe che sulle colonne debbono rispettare le ovvie relazioni:

0

I valori saranno, in generale, diversi per i due giocatori e possono essere interpretati come le probabilità con cui debbono essere estratte/scelte le strategie (se la giocata è unica), ovvero come le frequenze relative con cui giocare le varie strategie (se il gioco è iterato). Il teorema di Von Neumann del 1928, però non si limita a stabilire solo l'esistenza di queste strategie miste di equilibrio, ma ci indica anche la via con cui calcolarle, per entrambi i giocatori, assieme al Valore del gioco, risolvendo due sistemi di equazioni lineari. Indichiamo, per semplicità di notazione, con Xi le probabilità delle strategie dei pattugliatori con Uj le probabilità delle strategie degli incursori e con V1 e V2 i valori del gioco (anche se sappiamo come insegna Von Neumann che sarà V1 = V2 = V).

Sistema di equazioni per i pattugliatori:

Sistema di equazioni per gli incursori:

E' da osservare che la matrice dei coefficienti dei due sistemi sono una la trasposta dell'altra e coincidono con la matrice del gioco vista dalla parte dei due giocatori.

Prima di riportare la soluzione di questi due sistemi intendiamo ricordare un aspetto del Risolutore Excel non a tutti noto. Esso consente di risolvere non solo problemi di ottimizzazione, ma anche sistemi di equazioni (lineari e no): è sufficiente non indicare alcun valore nella cella obiettivo. In questo esempio (Vedi foglio: Strategie Miste MinMax dell'allegato file Excel) abbiamo addirittura risolto contemporaneamente i due sistemi di equazioni.

Soluzione: strategie miste per i pattugliatori:

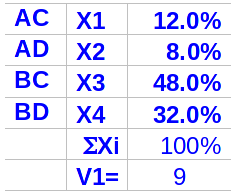
Soluzione: strategie miste per gli incursori:

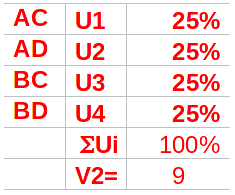
Questa soluzione numerica mi ha inizialmente stupito non tanto per la preferenza data alla strategia BC dei pattugliatori ( X3 = 48%) quanto per l'indifferenza tra le proprie strategie degli incursori (Uj = 25%). Una più attenta considerazione porta però a concludere che gli incursori nulla sanno delle strategie dei pattugliatori e pertanto per loro il comportamento più razionale è equiparare al 25% le proprie tattiche di incursione. Una altra considerazione deriva dal valore del gioco: V1 = V2 = V = 9. Questo significa: per i pattugliatori una probabilità di successo del 9/25 = 36% per gli incursori (1 - 9/25) = 64%.

Cosa possono fare i pattugliatori per far salire le probabilità di successo oltre il 36%?

  1. Cambiare la ripartizione 0.25 - 0.75 nelle tecniche di pattugliamento;
  2. Migliorare le caratteristiche tecniche dei propri sistemi di avvistamento;
  3. Istituire una terza o quarta linea di pattugliamento.

Programmazione lineare e dualità

Come già scritto nella introduzione fu Von Neumann, pensando al suo teorema del MiniMax, a segnalare a Dantzig l'ipotesi della teoria della dualità in P.L. quando questi gli illustrò il suo metodo del simplesso. Dantzig recepì immediatamente le informazioni e ideò un metodo alternativo per la PL chiamato Simplesso primale/duale che consentiva di risolvere contemporaneamente i due problemi gemelli: il primale e il duale. La teoria della dualità fu presto estesa e generalizzata, seppure in altre forme, alla programmazione quadratica e ad altri problemi di programmazione matematica da Tucker, Gale e Kuhn.

Si riporta sotto un esempio di problema di PL con il suo duale

Primale:

( \text{Min} \sum ci ast xi ) (i = 1 … n variabili)

( Aast X gt b ) (m vincoli)

( xi gt 0 )

Duale:

( \text{Max } \sum bj ast uj ) (j =1 … m variabili)

( B ast U lt c ) (n vincoli)

( uj gt 0 )

Di seguito alcune considerazioni qualitative:

  1. Ogni problema di PL ha un suo duale. Il duale di un problema ha il suo duale nel primale originario;
  2. il duale di un problema di massimizzazione è un problema di minimizzazione, e viceversa;
  3. se il primale ha n variabili ed m vincoli il duale ha m variabili ed n vincoli;
  4. vincoli di maggiore o uguale del primale diventano di minore o uguale nel duale e viceversa;
  5. la matrice di questi vincoli è una la trasposta dell'altra;
  6. i termini noti dei vincoli del primale diventano i coefficienti della funzione obiettivo del duale e i coefficienti della funzione obiettivo del primale diventano i termini noti dei vincoli del duale.
Con riferimento al punto 6) la teoria della dualità ha trovato feconda applicazione in economia per spiegare il concetto dei "prezzi ombra" delle risorse. Questi prezzi nulla hanno a che vedere con i prezzi di mercato delle risorse (uomini, mezzi, materiali e servizi). Essi si riferiscono infatti, in una specifica situazione problematica, al maggiore guadagno in più che si potrebbe ottenere se fosse disponibile una unità in più della specifica risorsa vincolante.

Torniamo al nostro problema di pattugliamento/incursione e vediamone la rappresentazione in termini di problema di P.L: primale/duale:

Punto di vista dei pattugliatori (problema primale):

Soluzione del primale:

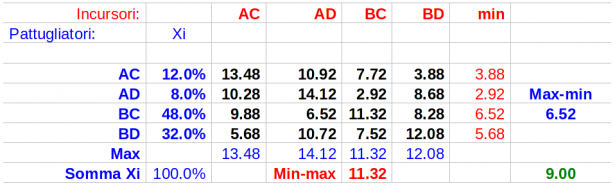
Punto di vista degli incursori (problema duale):

Soluzione duale:

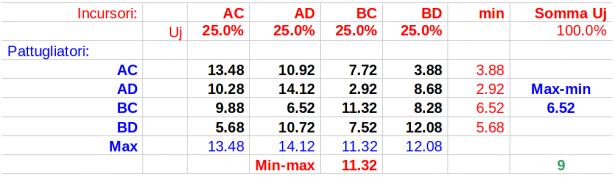
Con la programmazione lineare abbiamo ritrovato gli stessi risultati ottenuti risolvendo il sistema di equazioni previste dal teorema del MiniMax di Von Neumann.

Per chi volesse effettuare ulteriori simulazioni numeriche o ricerche su questi problemi può trovare nel file Excel allegato i seguenti fogli:

  • Strategie pure;
  • Strategie miste MinMax;
  • Prog. Lineare primale;
  • Prog. Lineare duale.

Conclusioni

"...le scienze non cercano di spiegare, a mala pena tentano di interpretare, ma soprattutto fanno dei modelli. Per modello si intende un costrutto matematico che, con l'aggiunta di certe interpretazioni verbali, descrive dei fenomeni osservati. La giustificazione di un costrutto matematico del genere è soltanto e precisamente che ci si aspetta che funzioni - cioè descriva correttamente i fenomeni di un area ragionevolmente ampia. Inoltre esso deve soddisfare certi criteri pratici ed estetici - cioè in relazione con la quantità di descrizione che fornisce, deve essere piuttosto semplice".

John Von Neumann (1903 -1957), Opere, vol 6, pag 492.

Con il progetto denominato EDVAC (Electronic Discrete Variable Automatic Computer ) Von Neumann diede, tra il 45 ed il 49, un grande contributo allo sviluppo dei computer. Nel rapporto preliminare venivano descritte cinque unità di base del calcolatore: l'unità di ingresso (per l'introduzione dei dati e dei programmi), l'unità di memoria (che immagazzinava i dati numerici e le istruzioni in codice binario), l'unità aritmetica (che provvedeva ad eseguire i calcoli previsti dal programma), l'unità centrale di governo (che controllava la sequenza delle operazioni e coordinava il funzionamento delle altre quattro unità), l'unità di uscita (per l'emissione dei risultati). Questa impostazione denominata 'architettura Von Neumann' costituisce ancor oggi, indipendentemente dal progresso tecnologico (tubi elettronici, transistor, circuiti integrati, microchip etc.) la struttura di base dei computer. Vedremo se in futuro si consolideranno nuove architetture, ad esempio le reti neurali, i computer paralleli o quelli quantici.
Per quanto riguarda lo sviluppo del software Von Neumann pubblicò tra il 47 ed il 48 il rapporto Planning and Coding Problems for an Electronic Computing Instrument che forniva un potente metodo per affrontare l'analisi dei problemi e l'approntamento dei programmi. I diagrammi di flusso (o schemi a blocchi) consentono di analizzare il problema in studio indipendentemente dal linguaggio di programmazione che sarà poi utilizzato (oggi si parla spesso di pseudo codice); di fatto questi diagrammi, magari con qualche modifica nella notazione, sono usati nelle organizzazioni anche per problemi che non implicano necessariamente un implementazione su computer (ad esempio l'analisi dei processi aziendali).

John Von Neumann

Riferimenti

Vuoi approfondire Applicazioni con un insegnante esperto?
Trovalo su Ripetizioni.it