Giochi non a somma zero e non cooperativi [John Nash]

Adam Smith va rivisto! ... Se tutti ci proviamo con la bionda, ci blocchiamo a vicenda. E alla fine… nessuno di noi se la prende. Allora ci proviamo con le sue amiche, e tutte loro ci voltano le spalle, perché a nessuno piace essere un ripiego. Ma se invece nessuno ci prova con la bionda, non ci ostacoliamo a vicenda, e non offendiamo le altre ragazze. È l'unico modo per vincere. ...L'unico modo per tutti di scopare!...Adam Smith ha detto che il miglior risultato si ottiene quando ogni componente del gruppo fa ciò che è meglio per sé, giusto? Incompleto.

"Negli anni 20 Emile Borel incominciò a studiare i giochi a due persone e a somma zero, in cui cioè quando qualcuno vince l'altro perde, cercando di dimostrare l'esistenza di equilibri. Si era reso conto che si trattava di una questione importante, ma pur essendo un matematico molto famoso e competente, non era più giovanissimo e non riuscì a risolverla. Chi lo fece fu Von Neumann, che ne parlò a un seminario a Gottingen e un paio di anni dopo pubblicò il suo famoso lavoro del 1928 in cui si dimostra l'esistenza di un equilibrio che può essere interpretato come un minMax: ogni giocatore ha una strategia perfettamente difensiva e la sceglie in maniera ottimale contro la strategia difensiva dell'altro giocatore.

Von Neumann e Morgestern generalizzarono il risultato a un numero qualunque di giocatori, ma sempre per giochi a somma zero. Nella mia tesi io estesi poi la generalizzazione a giochi qualunque, e i cosiddetti equilibri di Nash si riducono ai minMax di Von Neumann e Morgestern non appena si specifica che il gioco in questione è a somma zero."

".... Alcuni dei miei metodi sono stati quasi subito recepiti da Kenneth Arrow e Gerard Debreu. Più che fra le teorie, la relazione è fra i metodi di dimostrazione: sia Arrow che Debreu usarono il teorema del punto fisso di Kakutani, che io avevo già usato un anno o due prima per dimostrare l'esistenza di quello che oggi si chiama 'Equilibrio di Nash' . A me l'aveva suggerito David Gale: agli inizi io pensavo invece di usare il teorema del punto fisso di Brouwer."

"... In un articolo degli anni 30 Von Neumann aveva effettivamente usato il teorema del punto fisso di Brouwer: fu proprio quell'articolo a stimolare Shizuo Kakutani a sviluppare la sua versione , che poi io ho usato nella mia tesi".

A proposito di Von Neumann, lei lo ha mai incontrato? "Si a Princeton. Andai da lui, quando ormai la mia tesi era a buon punto. Lui ascoltò l'enunciato del mio teorema e mi chiese immediatamente se nella dimostrazione usavo un punto fisso. All'epoca rimasi sorpreso, ma quello che ho appena detto spiega, almeno in parte, la reazione di von Neumann.

E conferma anche la sua proverbiale velocità di pensiero? "Si. Ma non tanto quanto la storia che si racconta, a proposito del problema di calcolare la distanza percorsa da un ape che va avanti e indietro tra due treni che si avvicinano a velocità costanti note. Il trucco sta nel calcolare prima il tempo che i due treni impiegano ad incontrarsi, e poi la distanza percorsa dall'ape in quel tempo, ma dicono che von Neumann calcolò a mente in un attimo la somma della serie infinita dei percorsi dell'ape".

Che cos'è invece la disuguaglianza di Nash? "Ha a che fare con un mio lavoro di analisi degli anni 50, relativo ad un problema aperto sulle equazioni differenziali parziali ellittiche. Io ho avuto l'idea di collegarlo al problema analogo delle equazioni paraboliche, riuscendo a risolvere entrambi i casi. Nel corso di questo processo ho usato alcune disuguaglianze, che poi sono state chiamate col mio nome. Ma, nel frattempo, alla soluzione del problema per le equazioni ellittiche era gia arrivato indipendentemente Ennio De Giorgi, che mi ha battuto nell'obiettivo".

John Nash (1928), Intervistato da P.G. Odifreddi in "I matematici solitari". Mondadori 2009.

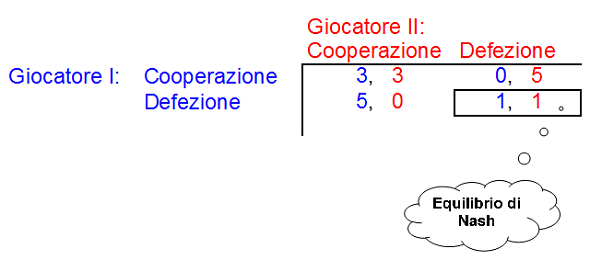
Il dilemma del prigioniero (Flood e Dresher, 1950) è forse il gioco di strategia più famoso e più diffuso dalle società di consulenza, dalle business school e dalle università americane, per descrivere le problematiche della competizione e della cooperazione. Due ladri vengono sorpresi, fermati, incarcerati ed interrogati in attesa del processo (pena prevista 5 anni). Sanno che se entrambi (cooperazione) negheranno ogni addebito per se e per il compare avranno entrambi uno sconto di pena pari a 3 anni; se, dichiarando la propria innocenza, si accuseranno reciprocamente (defezione) avranno uno sconto di solo 1 anno. Se uno solo decide di coprire il compare cooperando non avrà nessuno sconto di pena mentre l'altro che lo accusa avrà l'intera pena condonata. La matrice, riportata in figura, riassume la situazione problematica del dilemma. Il gioco (che non è a somma zero) ha un punto di equilibrio di Nash nella defezione di entrambi i giocatori (1,1). Se un solo giocatore proverà a scostarsi da esso cooperando cadrà nella situazione peggiore in cui non si ha alcuno sconto di pena. L'aspetto inquietante del gioco è dato dal fatto che proprio il punto di equilibrio stabile (1,1) è l'unico a non essere Pareto-ottimale cioè è l'unico ad essere dominato da un altro punto (3,3 che è migliore per entrambi i giocatori). Dunque la cooperazione, che è migliore per tutti, non è in questo gioco un punto di equilibrio. E' stato simulato al computer (R. Axelrod, The Evolution of Cooperation, Basic Books, New York 1984) che, nel Dilemma del prigioniero iterato, la strategia vincente non è ne quella di Defezione ad oltranza (1,1) ne quella di Cooperazione ad oltranza (3,3), ma è quella denominata "Tit for Tat" ovvero "Occhio per occhio, dente per dente": alla prima mossa collabora, alle successive copia la precedente del tuo avversario. (R. Chiappi, Il foglio elettronico come strumento per il problem solving, F.Angeli 2008).

Chi volesse approfondire gli aspetti teorici dei giochi o conoscerne le principali applicazioni può, in questo sito, leggere sul primo numero del Magazine l'articolo di F. Patrone: "Matematica d'oggi: la teoria dei giochi" oppure consultare sull'argomento il Forum da lui diretto.