Introduzione al Metodo Montecarlo

"Dio non gioca a dadi con l'universo".
Da una lettera di Albert Einstein a Niels Bohr
"...Ventisei tentativi hanno preceduto la Genesi attuale e tutti erano destinati a fallire. Il mondo dell'uomo uscito dal grembo caotico di questi detriti anteriori, e a sua volta non possiede alcun certificato di garanzia: anch'esso esposto al rischio del fallimento e del ritorno al nulla. Speriamo che funzioni! [Halway Sheyaamod] esclama Dio creando il mondo, e questa speranza accompagna tutta l'ulteriore storia del mondo e dell'umanit, sottolineando fin dall'inizio come questa storia segnata dal marchio della radicale incertezza".

Riferimento all'esegesi rabbinica - Bershit Rabba 9,4

(in : André Neher, L'esilio della parola, pag. 72)

Introduzione

L'origine del metodo Montecarlo viene solitamente associata alla nascita dei computer ed in particolare alle ricerche fatte da Fermi, Ulam e Von Neumann, nel secondo dopoguerra, sui processi di diffusione dei neutroni. Per la verità circa 150 anni prima Buffon aveva ideato un esperimento consistente nel lancio di un ago di lunghezza nota su un foglio in cui erano rappresentate rette parallele a distanza nota tra loro. Il lancio, ripetuto molte volte, dell'ago consentiva un calcolo approssimato di PI greco. Forse per questo motivo si è cominciato a dire che la simulazione Montecarlo consentiva alla matematica, regina delle scienze priva però della possibilità di fare esperimenti, di effettuare anch'essa i propri. Non vi per dubbio che il metodo ha potuto, visto l'elevato numero di replicazioni necessarie, affermarsi solo con la diffusione di computer sempre più veloci e a minor costo. È sorprendente che una tecnica probabilistica, come è questo metodo, si sia rivelata utile in problemi deterministici di calcolo numerico come la stima di integrali non calcolabili in forma chiusa. Fate il seguente esperimento mentale. Ritagliate da un grande cartone un quadrato avente un metro di lato. Da un punto di uno dei lati del cartone disegnate una linea qualunque, anche con massimi, minimi o punti angolosi, che termina in un punto qualunque del lato opposto del quadrato. Appendete il cartone ad un albero e procuratevi un fucile da caccia (cioè uno di quelli che ad ogni colpo sparano una nuvola di pallini di piombo). Posizionatevi a circa una ventina di metri dal cartone e, puntandolo, sparate una decina di colpi. Andate a prendere il cartone e, con pazienza contate il numero di fori che stanno sotto la linea tracciata (supponiamo 613) e quelli che stanno sopra la linea (supponiamo 380). Quale può essere una buona stima dell'area che sta sotto la curva? La risposta è straordinariamente semplice: 613/(613 + 380) = 613/993 = 0.6173 metri quadrati. Naturalmente nella realtà di oggi non servono cartoni, alberi o fucili da caccia. Qualunque computer dispone di un generatore di numeri casuali¹. È sufficiente, ad ogni iterazione generare due numeri casuali a cui corrisponderà un punto, nello spazio cartesiano, posizionato sotto o sopra la curva di cui volete calcolare l'integrale.

Il metodo Montecarlo ha un ruolo rilevante tra i metodi di simulazione stocastica che, assieme alla simulazione dinamica, costituisce uno dei più importanti capitoli della simulazione su computer.

Una volta si diceva che la simulazione costituisce l'ultima spiaggia dei matematici applicati: da usarsi quando tutto il resto fallisce. Oggi non è più così e la simulazione su computer (grazie ai continui miglioramenti di hardware e software), ed in particolare il metodo Montecarlo, costituisce uno dei più importanti strumenti disponibile ai matematici applicati per risolvere problemi. Citiamo tra questi: calcolo dei premi delle compagnie di assicurazione; regolazione dei semafori cittadini; dimensionamento del traffico telefonico; code o attese ai caselli autostradali, per gli esami clinici, o più banalmente in banca o dal barbiere; gestione degli ordini, del magazzino e della produzione; marketing e distribuzione; programmazione della manutenzione preventiva; gestione dei forni in una acciaieria; budgeting e finanza; rischio nelle durate e nei costi di un progetto; applicazioni militari, valutazione dei sistemi d'arma; gioco d'azzardo, ecc.

Gioco dazzardo, dadi e probabilità

Il nome Monte Carlo fu inventato, successivamente ai lavori di Ulam, Fermi, Von Neumann, da Nicholas Constantine Metropolis proprio in riferimento alla nota tradizione, nei giochi d'azzardo praticati nel casinò del mini stato omonimo situato nel sud della Francia. Può sembrare superficiale riferirsi a questi giochi eppure il calcolo delle probabilità nacque da problemi discussi e basati sull'esito del lancio dei dadi, basti citare: Cardano, Pascal, Fermat, Galilei, Huygens.

Le definizioni/concezioni di probabilità sono quattro:

• Classica (Pascal-Laplace): rapporto tra casi favorevoli e casi possibili (considerati equiprobabili);


• Frequentista (Von Mises): limite (all'infinito) del rapporto tra casi favorevoli e totali;


• Soggettivistica (De Finetti): stima, soggettiva, della probabilità di successo di un evento;


• Assiomatica (Kolmogorov): qualunque numero compreso tra 0-1 che rispetti definite proprietà.

Le prime tre definizioni sono costruttiviste indicano cioè una via per calcolare le probabilità, la quarta non lo è, ma indica gli assiomi a cui deve sottostare un sistema coerente di calcolo delle probabilità. Da osservare che le prime tre concezioni (Classica, Frequentista, Soggettivistica) soddisfano tutte le condizioni poste dai requisiti di coerenza della teoria Assiomatica.

Interessante ricordare che sul concetto di probabilità si sono esercitate alcune delle migliori menti, molti del secolo scorso, provenienti da contesti disciplinari assai diversi (sia umanisti che scientifici): matematici (Bayes, Kolmogorov, De Finetti), filosofi (Russell, Wittgenstein, Popper), economisti (Keynes, Von Mises); Fermat era un magistrato che si dilettava di matematica.

Lancio di un dado:

Iniziamo con il lancio di un dado non truccato. Le facce del cubo sono sei dunque le probabilità di uscita di ogni numero sono 1/6 = 16.666 %. Si osservi che per calcolare la probabilità abbiano implicitamente applicato la definizione Classica di probabilità: caso favorevole 1 casi possibili 6.

Esiti possibili 6:	Probabilità (1/6)	Cumulata
1	16.7%	16.7%
2	16.7%	33.3%
3	16.7%	50.0%
4	16.7%	66.7%
5	16.7%	83.3%
6	16.7%	100.0%
Totale	100.0%

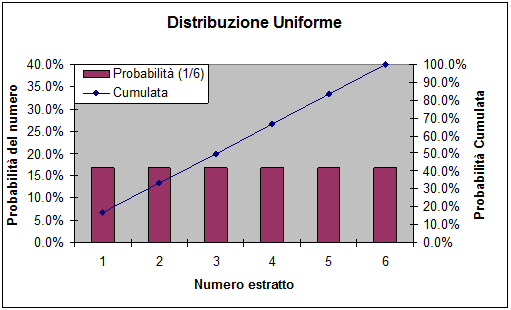
Abbiamo introdotto alcuni concetti importanti. L'istogramma, che rappresenta la probabilità di ciascun numero, si chiama distribuzione (o densità) della probabilità. Le funzioni di distribuzione della probabilità possono essere discrete (come nel gioco dei dadi, nella roulette, le persone in coda o servite, ecc.) oppure possono essere continue (altezze o peso delle persone, durata di una telefonata, di una attività, ecc.). L'istogramma riportato sopra rappresenta una distribuzione discreta uniforme (in cui tutti i valori hanno la stessa probabilità). Le distribuzioni uniformi, sia nel discreto che nel continuo (rappresentabili con un rettangolo) sono molto importanti perché a partire da esse e possibile generare distribuzioni di ogni tipo (ad esempio con il metodo di inversione della funzione cumulata). I fogli Excel consentono l'accesso a due generatori di numeri pseudo casuali uniformi: la funzione =Casuale() che genera numeri casuali uniformi distribuiti con continuità tra 0 ed 1 e la funzione Casuale.tra(n1;n2) che genera numeri discreti (interi) compresi tra n1 e n2. Questa seconda funzione è stata utilizzata nel workbook Excel (iterazioni) per simulare, con il metodo Montecarlo, il lancio di 1- 4 dadi.

Nel grafico riportato sopra la retta (tra 16.7% e 100%) rappresenta la funzione di ripartizione (o cumulata delle probabilità). Questa linea rappresenta il progressivo, da 1 a 6, delle probabilità del lancio di un dado. Nel linguaggio della analisi matematica rappresenta l'integrale della funzione di densità di probabilità (nell'esempio l'istogramma). La funzione di probabilità cumulata ha un utilizzo pratico ed importante perché serve, in molti casi, a misurare la probabilità di successo, mentre il suo complemento ad uno (la retro cumulata) serve a misurare la probabilità (o il rischio) d'insuccesso.

Lancio di due dadi:

Nel lancio di due dadi i risultati possibili (1 ovviamente non può uscire, perché si considera la somma) variano da due a dodici. Molte persone ritengono che anche in questo caso la distribuzione di probabilità sia uniforme, come nel lancio di un dado. Così non è, e per convincersene basta guardare la tabella riportata sotto che mostra tutti gli esiti possibili:

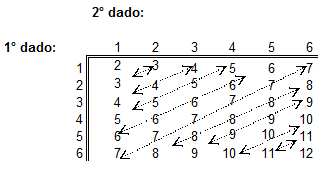Lancio di due dadi: (Somma valori)

E subito evidente che il 2 e il 12 possono uscire solo con una combinazione (1+1 e 6+6) mentre il 7 (che ha la probabilità massima) può uscire con 6 combinazioni diverse. Ecco sotto la tabella e il grafico della densità di probabilità e della funzione di ripartizione (o cumulata) calcolate per ogni Esito possibile.

Esiti possibili 11: (6x6=36 Combinazioni)	Probabilità	Cumulata
2	2.8%	2.8%
3	5.6%	8.3%
4	8.3%	16.7%
5	11.1%	27.8%
6	13.9%	41.7%
7	16.7%	58.3%
8	13.9%	72.2%
9	11.1%	83.3%
10	8.3%	91.7%
11	5.6%	97.2%
12	2.8%	100.0%
Totale	100.0%

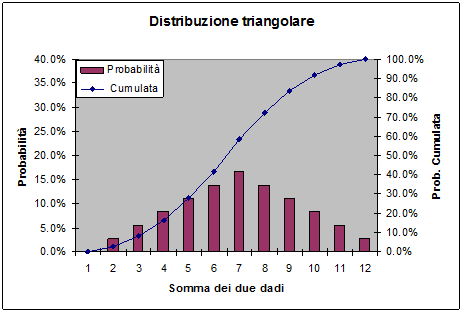
Dunque sommando due distribuzioni uniformi si ottiene una distribuzione triangolare.


Lancio di tre Dadi:

Si narra che un amico di Galileo Galilei, amante dei giochi di azzardo, fosse angustiato dal problema seguente: sebbene con un solo lancio di tre dadi si possa ottenere in totale 9 oppure 10 con lo stesso numero (6) di combinazioni (per esempio, 9 = 4+3+2 e 10 = 4+4+2), l'esperienza gli mostrava che 10 era un risultato leggermente più probabile di 9. La risposta, corretta di Galileo fu che dei 6^3 =216 modi possibili in cui tre dadi potevano cadere, un numero leggermente superiore di essi dava 10 rispetto a 9. In pratica l'amico trascurava le permutazioni che si possono avere all'interno di ciascuna combinazione. Oggi studenti, meritevoli, delle scuole medie hanno ripercorso l'elenco delle 216 possibilità computate da Galilei (vedi Bibliografia). Nel seguito ci limitiamo a riportare i risultati possibili con la funzione di densità e la cumulata.
lancio di tre dadi: (Somma valori)

Esiti possibili 16: (6x6x6=216 Combinazioni)	Probabilità	Cumulata
3	0.5%	0.5%
4	1.4%	1.9%
5	2.8%	4.6%
6	4.6%	9.3%
7	6.9%	16.2%
8	9.7%	25.9%
9	11.6%	37.5%
10	12.5%	50.0%
11	12.5%	62.5%
12	11.6%	74.1%
13	9.7%	83.8%
14	6.9%	90.7%
15	4.6%	95.4%
16	2.8%	98.1%
17	1.4%	99.5%
18	0.5%	100.0%
Totale	100.0%

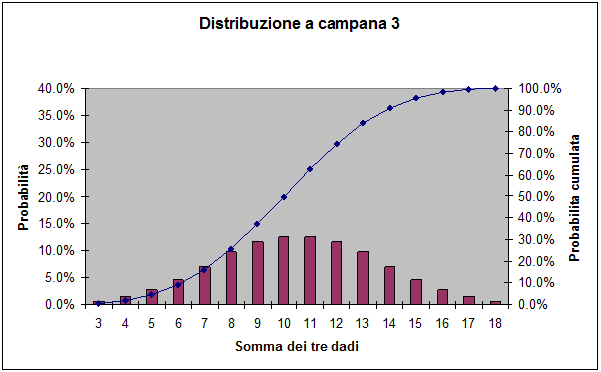
Dunque sommando tre distribuzioni uniformi si ottiene una distribuzione che assomiglia ad una campana.

Teorema del limite centrale

La distribuzione vagamente assimilabile ad una campana, già per il lancio di tre dadi (in generale per la somma di n variabili casuali), permette di introdurre uno dei più importanti teoremi della statistica e del calcolo delle probabilità, notevole non solo per la teoria, ma anche per le applicazioni pratiche del calcolo statistico/probabilistico. Si tratta del Teorema del limite centrale formulato inizialmente da de Moivre e poi generalizzato da Laplace. Per una definizione rigorosa del teorema si rimanda a qualunque manuale di calcolo delle probabilità o più semplicemente a Wikipedia. Qui è sufficiente comprenderne il significato e la portata. Così recita il teorema: se una variabile casuale s è somma di n variabili casuali allora la distribuzione di densità di s tende, al tendere di n all'infinito, alla distribuzione Normale (o Campana di Gauss) avente per media la somma delle medie delle singole distribuzioni e per varianza la somma delle varianze delle singole distribuzioni componenti la somma (Varianza = Scarto quadratico medio^2). L'aspetto pratico/operativo, interessante del teorema è che già per n uguale a 20 variabili la distribuzione somma è molto vicina ad una distribuzione Normale. Inoltre se le distribuzioni sono simmetriche rispetto alla mediana (il valore centrale della distribuzione sull'asse delle ascisse) e se le distribuzioni hanno media e scarto dello stesso ordine di grandezza allora è sufficiente che n sia uguale a 4-5 per avere una distribuzione somma molto vicina ad una distribuzione a campana e quindi alla Normale di Gauss.

Workbook Excel (Iterazioni) per il lancio simulato dei dadi con il metodo Montecarlo:

Solitamente per illustrare il metodo Montecarlo con Excel (vedi in bibliografia i link a Project Ware e a Project Management Center) si usa memorizzare ogni replicazione in una riga del foglio. Ci dipende dal fatto che in Excel non sono permessi riferimenti circolari tra le celle e quindi tantomeno sono permessi accumulatori del tipo X = X +1 in una unica cella. Questo limite, proprio di tutti i fogli di calcolo, può essere superato ricorrendo al Men: Strumenti, Opzioni, Calcolo, consentendo le iterazione e ponendo a 1 il numero di esse. In questa maniere si evita il messaggio di errore Riferimenti Circolari e si consente agli accumulatori degli esiti dei lanci di funzionare (Vedi Workbook Iterazioni).

La simulazione può essere fatta passo, passo. Al primo lancio (effettuato inserendo 1 nella cella E1) l'istogramma andrà fuori scala in quanto il 100% concentrato in un solo esito e il fondo scala degli istogrammi è stato posto al 40%. Dopo alcuni lanci, effettuati premendo ripetutamente F9 Ricalcolo, l'istogramma rientrerà nella scala prefissata. Se invece si desidera simulare il lancio di dadi in rapida successione è sufficiente mantenere premuto il tasto F9. La velocità dipende dal computer e dalla versione Excel che avete, con il mio effettuare 1000 lanci richiede circa 35 secondi, cioè, più o meno, 29 lanci al secondo. È sempre possibile lanciare una simulazione, sospenderla e riprenderla in un altro momento, come è possibile in ogni momento ripartire con una² sequenza nuova: E1 = 0. Questo workbook consente di iniziare a toccare con mano l'affermazione che il metodo Montecarlo, implementato su computer, permette di effettuare esperimenti matematici, altrimenti impossibili a questa disciplina. Tempo addietro sul Forum di www.matematicamente.it appariva questa discussione: Quanti lanci di due dadi debbo effettuare perché il numero 7 prevalga?. Potete cercare di trovare la risposta sperimentando, con il foglio relativo a due dadi, il metodo Montecarlo. A Galileo fu chiesto: Nel lancio di tre dadi il 10 è più probabile del 9?. Cercate la risposta sperimentalmente con il foglio relativo a tre dadi, Galileo non poteva sperimentare perché all'epoca i computer non erano disponibili. Con semplicità possono essere aggiunti a questo Workbook altri fogli per simulare il lancio di 5, 6 10 dadi. Se vi diverte provate a farlo, vedrete che la curva di densità di probabilit si approssimerà sempre di più alla curva Normale di Gauss.

Lancio di 4 dadi. Applicazione a un progetto fortemente incerto.

Se i dadi sono 4 Le possibilità diventano 6^4 = 1296, decisamente un po' troppe da enumerare a mano, forse non basterebbe la pazienza di Galileo. Qualcosa si può per subito dire sugli esiti possibili della somma dei dadi lanciati: minimo 4, massimo 6x4 =24, inoltre poiché si tratta sempre di distribuzioni simmetriche (media, mediana e moda coincidono), il risultato più probabile : (4+24)/2 = 28/2 =14 che può avvenire in 146 modi diversi; dunque la sua probabilità è di 146/1296 = 11.265 %. (vedi il libro di Paul J. Nahin citato in bibliografia).

Per dare un minimo di concretezza a questi discorsi e andare oltre il mero gioco dei dadi si consideri il seguente progetto costituito da quattro fasi, fortemente incerte, da eseguirsi in serie una dopo l'altra.



Le quattro fasi hanno tutte una Durata (Du) incerta che può andare da uno a sei mesi in dipendenza di alcuni test che se di esito negativo possono costringere a lunghi rifacimenti. Per essere più precisi diciamo che ciascuna fase sarà completata entro un mese con probabilità 1/6, entro due mesi con probabilità 2/6, entro 3 mesi con probabilità 3/6, entro 4 mesi con probabilità 4/6, entro 5 mesi con probabilità 5/6, entro 6 mesi con certezza. Il Committente del progetto garantisce all'appaltatore, che accetti di realizzarlo, margini molto consistenti, ma pone penali assai rilevanti se la durata del progetto dovesse superare i 20 mesi. Queste penali non solo azzererebbero tutti i margini, ma rischierebbero di mandare in rosso l'appaltatore. Il direttore commerciale della potenziale società appaltatrice ha molte riserve sul progetto e così le esprime al suo amministratore delegato.

La probabilità di terminare i lavori nei tempi contrattuali è di 20/24 = 83.33% dunque il rischio di non farcela è del 16.66%. Non possiamo permettere che la nostra azienda lavori per quasi due anni ad un progetto così impegnativo che ha un rischio di quasi il 17% di mandarci in rosso. Per scrupolo il direttore commerciale si riserva di far fare una analisi Montecarlo, sui tempi di completamento, al Risk Manager e di tornare poi, con i risultati più precisi, dall'amministratore delegato.

Il Risk Manager riconosce immediatamente che il calcolo della distribuzione di densità della durata del progetto, della cumulata e del conseguente rischio di non farcela è assimilabile al problema del lancio di quattro dadi infatti ciascuna fase del progetto, assimilabile ad un dado, può durare, con distribuzione uniforme da uno a sei mesi³. Con facilità prepara l'analisi Montecarlo richiesta effettuata su circa 10,000 replicazioni.





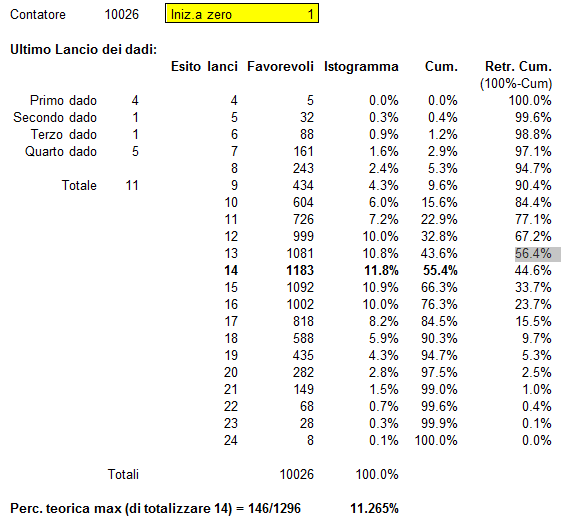
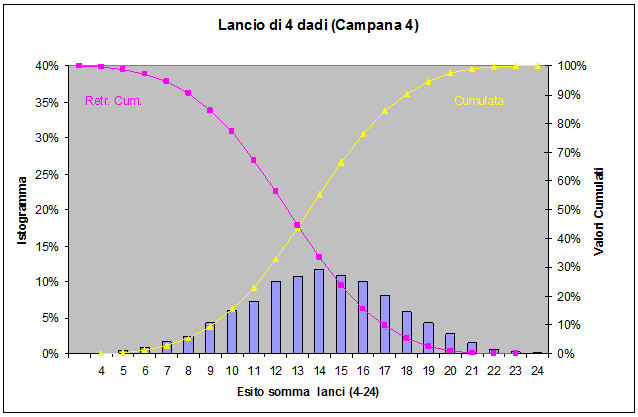
Il direttore commerciale, vedendo i risultati riconosce subito il suo errore, ma al contempo è piuttosto soddisfatto. L'errore stato evincere che se le sei fasi hanno distribuzione uniforme delle durate sui 6 mesi, anche il progetto, nella sua totalità, ha una densità di probabilità uniforme sui 24 mesi. I tempi dell'università erano lontani, e si era del tutto dimenticato del teorema del limite centrale studiato con l'esame di statistica. La soddisfazione deriva dal fatto che la probabilità di completare il progetto entro 20 mesi è di circa 97.5%, mentre il rischio di non farcela è solo del 2.5%. Chiede subito alla segretaria dell'amministratore delegato di poterlo incontrare per illustrargli i risultati ottenuti con l'analisi Montecarlo.

Bibliografia:

• Ludovico Piccinato, "La Simulazione", Istituto del Calcolo delle probabilit, Roma 1967.


• R.J, Thierauf, R.C. Klekamp, "Decision Making Through Operations Research", Wiley, New York 1970.


• Pierangelo Cignoli, "Introduzione alla Simulazione", Giappichelli, Torino 1976.


• Walter De Ambrogio, "Programmazione Reticolare", Etas Libri, Milano 1977.


• Bruno Martinoli, "Guida alla Simulazione", F. Angeli, Milano 1988.


• Bruno de Finetti, Filosofia della probabilit, Il Saggiatore, Milano 1995.


• A.N. Kolmogorov, Teoria delle probabilit, Teknos, Roma 1995.


• Stefano Fabi, "Una introduzione all'analisi MonteCarlo in finanza", 1998


• Roberto Chiappi, "Tecniche di General Management", Scuola Mattei, S.Donato 2001.


• Istituto Ivana Niccolai, Giocando con tre dadi non truccati, Classe VB, 2006/07


• YouTube, "Tutorial Metodo MonteCarlo con MS Excel", 2011


• Nicola De Nitti, "Casualità Matematica e metodo MonteCarlo", Matematicamente.it, Il Magazinie Sett. 2013.


• Project Ware: MonteCarlo Simulation in MS Excel


• Project Management Center, "Simulazione MonteCarlo con MS Excel, 2015


• ITIS Galilei, "Simulare con il metodo MonteCarlo", Crema


• Paul J. Nahin, "Sarai ancora vivo tra 10 anni? E molte altre curiose domande di probabilità",U. Hoepli, Milano 2015

---

Note

1. In realtà questi generatori, essendo guidati da un algoritmo deterministico forniscono dei numeri pseudo-casuali che prima o poi si ripetono ciclicamente. Quanto più lungo è il periodo del ciclo tanto migliore è la qualità del generatore. Altra caratteristica di un buon generatore è la sua velocità nel generare i numeri (oggi si parla anche di un miliardo di numeri al secondo).


2. Si osservi che una nuova sequenza non ripete gli stessi numeri casuali, in quanto i generatori sono inizializzati con un seme sempre diverso (preso, ad esempio dall'ora e dalla data segnata dall'orologio del computer)


3. A rigore, in questo caso, invece di usare =Casuale.tra(1,6), che genera numeri interi, sarebbe opportuno usare =Casuale()*(6-1) + 1 che genera valori continui compresi tra 1 e 6 mesi. L'approssimazione è comunque accettabile.