Essi sono sempre risolvibili quando sia possibile esprimere le relazioni che legano fra loro le variabili con espressioni (equazioni e disequazioni) lineari.
La direzione di uno stabilimento metalmeccanico, appartenente ad una media impresa a gestione familiare operante negli anni 70, deve impostare il proprio programma annuale di produzione. Attraverso ricerche, condotte dall'ufficio Marketing, si è individuata una certa gamma di prodotti (P), per ciascuno dei quali si è poi determinato il limite presunto di Assorbimento (A) in corrispondenza di un prefissato prezzo di vendita. I tecnici hanno messo a punto le analisi di costo e di fattibilità (attrezzature e macchinari disponibili, capacità tecnica del personale, risorse finanziarie, tempistica di approvvigionamento per semilavorati e componenti di produzione esterna, ecc.).
Dopo alcune riunioni, si è deciso di fissare l'attenzione su sei prodotti per ciascuno dei quali, nella tabella sottostante sono riepilogati: Guadagno netto (G) realizzabile per unità prodotta, limite massimo di Assorbimento del mercato (A), Tempi di lavorazione (T) occorrenti per la produzione di un' unità (suddivisi per ciascuno dei tre Reparti principali (R) che costituiscono lo stabilimento):
| Prodotti | Guadagni | Mercato | Tempi R1 | Tempi R2 | Tempi R3 |
|---|---|---|---|---|---|
| G (ML/n) | A (10^3n) | T1 (h/n) | T2 (h/n) | T3 (h/n) | |
| P1 | 3.0 | 10 | 3.5 | 2.0 | 4.0 |
| P2 | 4.0 | 8 | 3.0 | 3.0 | 4.2 |
| P3 | 5.0 | 30 | 4.0 | 2.8 | 3.5 |
| P4 | 3.5 | 16 | 5.0 | 1.5 | 2.5 |
| P5 | 4.0 | 25 | 2.8 | 5.0 | 3.0 |
| P6 | 2.8 | 5 | 1.7 | 1.5 | 2.0 |
| Capacità R | |||||
| ( 10^3 ore) | 200 | 160 | 400 |
200,000; 160,000; 400,000 ore. La direzione dello stabilimento si rende benissimo conto che i rapporti fra le capacità produttive dei tre reparti non sono ottimali per i cicli di lavorazione richiesti dalla nuova gamma di prodotti; tuttavia richiede, all'ufficio di Ricerca operativa dell'azienda, di elaborare il programma di produzione cui corrisponde il massimo guadagno.
Il problema è evidentemente di programmazione lineare. Oggi esistono vari algoritmi che fanno riferimento anche ai punti interni della regione ammissibile (Khachiyan, Karmarkar, ecc.) che hanno complessità polinomiale, ma il metodo del Simplesso di Dantzig, che lavora solo sui vertici del poliedro convesso e che nel caso peggiore ha complessità esponenziale, risulta in media ancora molto efficiente; infatti i fogli elettronici come Excel continuano ad adottarlo.
Ecco come, nel nostro caso, l'ufficio di Ricerca Operativa dell'azienda ha formalizzato il problema chiamando Z la funzione obiettivo da massimizzare ed impostando il sistema vincolante esprimendo i Guadagni in Milioni di Lire, le Produzioni in Migliaia di pezzi e le capacità produttive dei singoli Reparti in Migliaia di ore:
Obiettivo
Max Z ! con: Z = 3*P1 + 4*P2 + 5*P3 + 3.5*P4 + 4*P5 + 2.8*P6Vincoli sui Prodotti
0 0 0 0 0 0Vincoli sui Reparti
R1) 3.5*P1 + 3*P2 + 4*P3 + 5*P4 + 2.8*P5 + 1.7*P6 R2) 2*P1 + 3*P2 + 2.8*P3 + 1.5*P4 + 5*P5 + 1.5*P6 R3) 4*P1 + 4.2*P2 + 3.5*P3 + 2.5*P4 + 3*P5 + 2*P6Soluzione con il metodo del Simplesso
Valori Ottimali della funzione obiettivo, delle Produzioni e dell'impegno dei Reparti:
| 244.88 | Z funzione obiettivo | (Milioni Lire) |
| N° Pezzi | Produzione ottimale e mercato |
|---|---|
| (Migliaia) | |
| P1 = 9.49 | Al massimo consentito dal mercato |
| P2 = 8.00 | Al massimo consentito dal mercato |
| P3=30.00 | Al massimo consentito dal mercato |
| P4 = 0.00 | Non viene prodotto |
| P5 = 5.11 | A 1/5 dei limiti del mercato |
| P6 = 5.00 | Al massimo consentito dal mercato |
| Tot = 57.6 | Totale Produzione |
| Ore Impegno | Sfruttamento risorse Reparti |
|---|---|
| (Migliaia) | |
| R1 = 200 | Al massimo |
| R2 = 160 | Al massimo |
| R3 = 202 | 198 Migliaia di ore non utilizzate |
Il direttore delle vendite chiede come mai nella soluzione ottimale il Prodotto P4 non venga incluso benché il suo Guadagno unitario (3.5) sia superiore sia a quello del Prodotto P1 (3) che a quello del Prodotto P6 (2.8) che invece sono inclusi nel piano annuale ottimale. Il responsabile R.O. spiega che non bisogna guardare solo i Guadagni unitari nella funzione obiettivo, ma anche l'impegno di risorse che i vari Prodotti richiedono. In particolare il Prodotto P4, per ogni pezzo prodotto, impegna (5) le risorse del Reparto 1 (che è saturato) ben più dei prodotti P1 (3.5) e P6(1.7).
Sul tema della saturazione dei Reparti, chiede la parola il direttore della produzione ponendo l'accento sul fatto che il problema dell'azienda è il sovradimensionamento del terzo Reparto (R3) che ha circa la metà delle sue risorse inutilizzate. La sua direzione ha studiato un piano di ridimensionamento di R3 che dovrebbe portare ad un taglio dei costi, consentendo un risparmio di circa 30 Milioni all'anno. Il problema, a suo dire, è che il piano implica inevitabilmente un elevato numero di esuberi tra le maestranze di R3, cosa poco gradita alla stessa proprietà che ha un implicito patto di solidarietà con il territorio circostante.
Il direttore della programmazione e analisi degli investimenti illustra invece un progetto di ristrutturazione globale dell'azienda che prevede il trasferimento di personale, macchinari e attrezzature da R3 (sovradimensionato) a R1 ed R2 (saturati). Il piano è ambizioso perché richiede: corsi di formazione per le maestranze e adattamento/acquisti di macchinari e attrezzature. Il suo costo secondo stime preliminari, ma attendibili, è piuttosto elevato, circa 300 Milioni di lire.
L'amministratore delegato, assistito dal direttore finanziario, vuole esplorare questa seconda soluzione e per questo chiede all'ufficio ricerca operativa di definire meglio come dovranno essere ridimensionati i tre Reparti, in termini di capacità produttive, ed inoltre chiede di valutare se la spesa di 300 Milioni potrà essere riassorbita, solo con i maggiori introiti derivanti dalla ristrutturazione, nell'arco di 6 anni tenendo anche conto degli oneri finanziari (presumibilmente al 4%).
Ristrutturazione
Una settimana dopo l'ufficio R.O. illustra i risultati ottenuti.La premessa è che in qualunque programma matematico (lineare o no) se si pongono vincoli più restrittivi, o se se ne aggiungono di nuovi, la funzione obiettivo potrà solo restare invariata o peggiorare. Al contrario se si rilasciano dei vincoli, o addirittura se ne tolgono, la funzione obiettivo potrà solo restare invariata o migliorare. Fortunatamente ci si trova in questo secondo caso. Nel nuovo modello di P.L. denominato "Ristrutturazione" sono stati infatti eliminati i tre vincoli sulle ore massime dei singoli reparti (lasciando all'algoritmo del simplesso il calcolo del loro dimensionamento ottimale), ma è stato inserito un vincolo totale per i tre reparti di 760,000 ore, questo per ottemperare al mandato della direzione che non vuole licenziamenti, ma neanche nuove assunzioni. Ecco i risultati che indicano: il nuovo valore della funzione obiettivo, le quantità di prodotti, che osservano comunque i limiti di assorbimento del mercato, e il nuovo dimensionamento dei reparti:
| 325.85 | Z Ristrutturazione | (Milioni Lire) | |
| 244.88 | Z Vecchia | (Milioni Lire) | |
| 80.97 | Differenza annua | (Milioni Lire) |
| N° Pezzi | Produzione ottimale e mercato |
|---|---|
| (Migliaia) | |
| P1 = 0.00 | Non viene prodotto |
| P2 = 8.00 | Al massimo consentito dal mercato |
| P3=30.00 | Al massimo consentito dal mercato |
| P4=16.00 | Al massimo consentito dal mercato |
| P5=18.46 | Al 74% dei limiti del mercato |
| P6 = 5.00 | Al massimo consentito dal mercato |
| Tot = 77.46 | Totale Produzione |
Per quanto concerne la richiesta della direzione di verificare dopo quanti anni potranno rientrare le spese di 300 milioni di lire necessarie per la ristrutturazione, il responsabile R.O. fa osservare che questo valore deve essere confrontato con il progressivo attualizzato dei maggiori introiti dovuti alla ristrutturazione, infatti la valutazione del Pay back attualizzato consente di tener conto implicitamente degli oneri finanziari. In proposito vengono presentate due Slides:
| Valore Attualizzato Progressivo | ||
| dei vantaggi della ristrutturazione: | ||
| Tasso di interesse = | 4% | |
| Numero anni | Val. At. | |
| (Milioni L.) | ||
| 1 | 77.86 | |
| 2 | 152.72 | |
| 3 | 224.70 | |
| 4 | 293.91 | |
| 5 | 360.46 | |
| 6 | 424.45 | |
| 7 | 485.98 | |
| 8 | 545.15 | |
| 9 | 602.04 | |
| 10 | 656.74 |
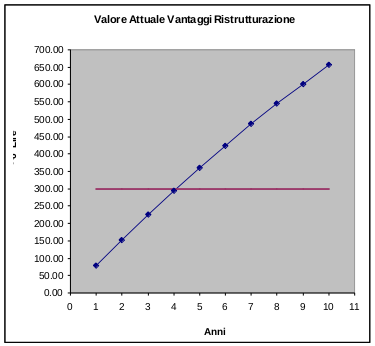
Dal grafico si può facilmente osservare che già nei primi mesi del 5° anno potranno essere recuperati integralmente i 300 milioni necessari alla riconversione delle maestranze e dei reparti pagando interessi al 4%: dunque parecchio prima dei 6 anni imposti come limite massimo dalla direzione. L'amministratore delegato si impegna a riferire i risultati delle ricerche alla proprietà. Alle ore 18 la riunione si chiude.
Dal foglio Excel si possono scaricare i dati "Iniziali", la soluzione "Ottima" ed i risultati della "Ristrutturazione".
(Fai click sull'icona in basso a destra per visualizzare la cartella di lavoro a pagina intera)
Riferimenti
- U. De Simoni, R. Chiappi, "La decisione motivata", non pubblicato, Ivrea 1976.
- F. Hillier, G. Lieberman, "Introduction to Operations Research", Holden Day, San Francisco 1969.
- R. Chiappi , "Il Foglio Elettronico come strumento per il Problem Solving", Angeli, Milano 2008.


