Programmazione lineare

Ogni industria si trova a dover fronteggiare problemi connessi con la distribuzione dei suoi prodotti finiti. Per industrie che producono beni di largo consumo, quali le industrie petrolifere, alimentari e farmaceutiche i costi connessi alla distribuzione dei prodotti possono rappresentare anche il 30% dei costi totali.

Introduzione

"…After my talk the chairman called for discussion. For a moment there was silence; then an hand raised. It was Hotelling's. I must explain that Hotelling was huge. He used to love to swim in the ocean and when he did, it is said the level of the ocean rose perceptively. This huge whale of a man stood up in the back of the room. His expressive face took on one of those of all-knowing smiles that we all know so well. He said devastingly: "But we all know the world is non -linear". Then he majestically sat down . And there I was, a virtually unknown, frantically try to compose a proper reply to great Hotelling.
Suddenly an other hand in the audience was raised. It was Von Neumann. "Mr Chairman, Mr. Chairman!" he said, if the speaker das not mind I would reply for him. Naturally I agreed . Von Neumann said: "The speaker titled his talk "Linear Programming". Then he carefully stated his axioms. If you have an application that satisfies the axioms use it. If does not then don't" and then he sat down .
In the final analysis of course, Hotelling was right. The world is highly non linear . Fortunately systems of linear inequalities (as opposed to equalities) permits us to approximate most of the kinds of non-linear relations encountered in practical planning.
The advent or rather the promise of the electronic computer, the exposure of theoretical mathematicians and economists to real problems during the war, the interest in mechanizing the planning process, and the availability of money for such applied research all converged during the period 1947-49…".
(George B. Dantzig, "Reminiscences About the Origins of Linear Programming", Operations Research Letters, North Holland, 1982)

Distribuzione

Ogni industria si trova a dover fronteggiare problemi connessi con la distribuzione dei suoi prodotti finiti. Per industrie che producono beni di largo consumo, quali le industrie petrolifere, alimentari e farmaceutiche i costi connessi alla distribuzione dei prodotti possono rappresentare anche il 30% dei costi totali.
Uno dei problemi che si presenta in questo campo è quello della determinazione del numero e della ubicazione ottimale dei depositi periferici. Può essere vantaggioso disporre di un certo numero di depositi perché ciò diminuisce i costi di trasporto ed aumenta il livello di servizio ai clienti. D'altro canto, a favore di un ristretto numero di grossi depositi, vi è l'esigenza di minimizzare i costi di installazione e mantenimento dei depositi stessi.
Un classico problema di ottimizzazione dei costi di trasporto fu quello affrontato nel 1958 a Mosca. Si trattava di determinare un programma ottimale per il trasporto di sabbia ai molti cantieri della città. Vi erano 10 origini e 230 destinazioni; la soluzione ottenuta dal computer "Strela" mediante un algoritmo di P.L. specializzato nei trasporti (Stepping-stone) portò ad un risparmio dell'11% circa, in un periodo di soli 10 giorni. Problemi più generali, che comprendano anche la localizzazione dei depositi, possono essere risolti con la Programmazione Lineare a Numeri Interi. Queste tecniche, accanto ad altre di simulazione, hanno fornito nel 1971 ad una grande azienda alimentare italiana, una rete di distribuzione che prevedeva una drastica riduzione del numero dei depositi rispetto a quelli esistenti, con una economia annua di alcune centinaia di milioni di Lit., a parità di livello di servizio ai clienti.

Caso 1: Raffinerie, Depositi, Punti vendita

Consideriamo l'esempio di due raffinerie (R1,R2) che alimentano tre depositi (C3,C4,C5) che devono rifornire cinque punti di domanda/vendita (d6, d7, d8, d9, d10).
I parametri del sistema sono: le domande dei cinque punti di vendita (d), le capacita dei depositi (C,c) e le potenzialità produttive delle raffinerie che devono essere comprese tra un massimo (Q) ed un minimo (q). Nel grafo riportato sull'allegato foglio Excel tutti questi parametri possono essere cambiati, ad esempio possono essere annullate le scorte di sicurezza (c) sui depositi.
Supponendo che i costi di produzione delle due raffinerie siano identici, e che pure identici siano i costi di stoccaggio nei depositi (limitazione che tra l'altro si può facilmente rimuovere) il problema si riduce a minimizzare i costi di trasporto Raffinerie-Depositi e Depositi-Punti di distribuzione.
Perché il problema abbia soluzione è necessario ovviamente che la somma delle domande (d) dei punti di distribuzione sia compresa tra la somma delle capacità Massime (C) e minime (c) dei depositi e la somma delle capacità Massime (Q) e minime (q) delle raffinerie. E' comunque interessante osservare che il Risolutore Excel, qualora queste condizioni non siano soddisfatte, oltre ad indicare che non esiste una soluzione fattibile, indica quello che è riuscito a fare.



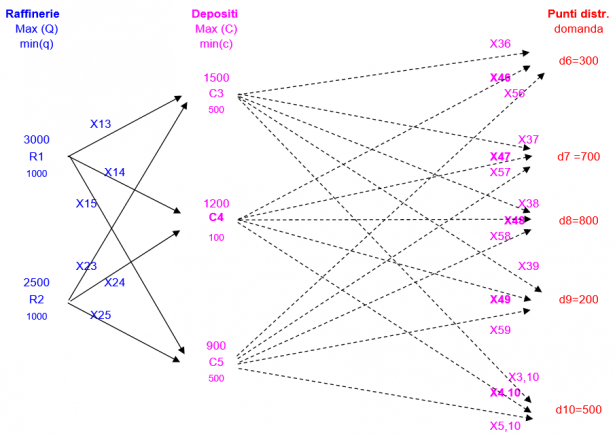
Introducendo dunque le quantità trasportate Xij, i costi di trasporto unitari Cij e le produzioni p1, p2 delle due raffinerie avremo il seguente modello matematico di programmazione lineare

Funzione obiettivo, minimizzare i costi totali di trasporto Raffinerie-Depositi e Depositi-Domanda:






Vincoli sulla produzione (p1 e p2) delle Raffinerie:

p1 = X13+X14+X15 <= Q1
p1 = X13+X14+X15 >= q1

p2 = X23+X24+X25 <= Q2
p2 = X23+X24+X25 >= q2

Vincoli di bilancio e scorta minima (c3,c4,c5, che può anche essere nulla) sui Depositi:

X13+X23 - (X36+X37+X38+X39+X3,10) >= c3
X14+X24 - (X46+X47+X48+X49+X4,10) >= c4
X15+X25 - (X56+X57+X58+X59+X5,10) >= c5

Vincoli di Capacità Massima (C1, C2, C3) sui Depositi:

X13+X23 <= C3
X14+X24 <= C4
X15+X25 <= C5

Vincoli di soddisfazione della domanda (d6,d7,d8,d9,d10):

X36+X46+X56 = d6
X37+X47+X57 = d7
X38+X48+X58 = d8
X39+X49+X59 = d9
X3,10+X4,10+X5,10 = d10

Vediamo ora il risultato che ci fornisce il Risolutore Excel in cui sono state scelte le opzioni: Modello lineare, Variabili Positive (Cioè metodo del Simplesso).

Variabili e Funzione Obiettivo (Costi totali, da minimizzare)



Dunque il Costo minimo (5000) si ottiene trasportando i quantitativi indicati in tabella tra le raffinerie e i depositi e poi tra i depositi e i punti di consumo finali.
Per chi volesse effettuare altre analisi con il Risolutore si consiglia per prima cosa di azzerare le Xij e poi di lanciare l'opzione "Risolvi". Se tutto è in ordine si deve nuovamente ottenere il Costo minimo 5000. Dopo aver effettuato questa prova di funzionamento si possono azzerare nuovamente le Xij, cambiare i dati ed effettuare nuove analisi.

Vincoli sulla produzione (p1 e p2) delle Raffinerie:



Si può osservare che la Produzione (p) delle due Raffinerie è compresa tra i limiti minimi (q) e Massimi (Q) consentiti.

Vincoli di bilancio e scorta minima (c3,c4,c5) sui Depositi:



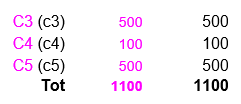
I requisiti di scorta minima sui tre depositi sono interamente soddisfatti.

Vincoli di Capacità Massima (C1, C2, C3) sui Depositi:

Le Capacità dei depositi sono sfruttate al massimo come mostra la tabella soprastante.

Vincoli di soddisfazione della domanda (d6,d7,d8,d9,d10): d6 (d6)



La domanda dei singoli punti di consumo (d6…d10) è interamente soddisfatta.
In definitiva possiamo riassumere dicendo che, rispettando tutti i vincoli, le raffinerie producono 3600 tonnellate di cui 2500 per soddisfare la domanda e 1100 per mantenere le scorte di sicurezza. I costi totali di trasporto sono minimizzati al valore 5000.

Caso 2: Localizzazione dei Depositi

Un'azienda produttrice di beni di largo consumo ha il problema di ristrutturare la sua rete di distribuzione che provvede a rifornire tutti i punti di vendita dislocati nella regione. Essendo nota l'ubicazione geografica dei punti di vendita, le possibili sedi dei magazzini, i costi di istallazione e le possibili vie di rifornimento (determinate precedentemente da vincoli geografici, economici, organizzativi, ecc.), si vuole ricercare il numero e la ubicazione dei depositi da costruire in modo da minimizzare i costi totali di installazione mantenimento e trasporto sul territorio. A questo scopo accanto alle 7 ubicazioni possibili dei depositi e stato indicato [tra parentesi quadre] un indicatore, compreso tra 0-10, che riassume la diversa onerosità di stabilire un deposito in quello specifico sito.
Il problema può essere formalizzato introducendo 7 varabili bivalenti (0 se non si fa il deposito 1 se si fa) X1,…X7. Inoltre debbono essere introdotti 20 vincoli per garantire che ciascuno dei punti vendita (pi) sia alimentato da almeno un deposito:

p1) X1 >= 1
p2) X1 >= 1
p3) X1 + X3 >= 1
p4) X1 + X2 >= 1
p5) X1 + X2 + X6 >= 1
p6) X2 + X3 + X5 >= 1
p7) X1 + X3 + X4 >= 1
p8) X4 >= 1
p9) X3 + X4 >= 1
p10) X3 + X4 +X7 >= 1
p11) X4 + X7 >= 1
p12) X4 + X5 >= 1
p13) X3 + X5 >= 1
p14) X2 + X5 + X6 >= 1
p15) X1 >= 1
p16) X1 + X5 + X6 + X7 >= 1
p17) X5 + X7 >= 1
p18) X2 + X3 + X7 >= 1
p19) X1 + X2 >= 1
p20) X4 >= 1

Xi = 0 o 1 (i = 1,…7)

F. Obiettivo: min {2X1 + 3X2 + X3 + X4 +6X5 + 2X6 + X7}



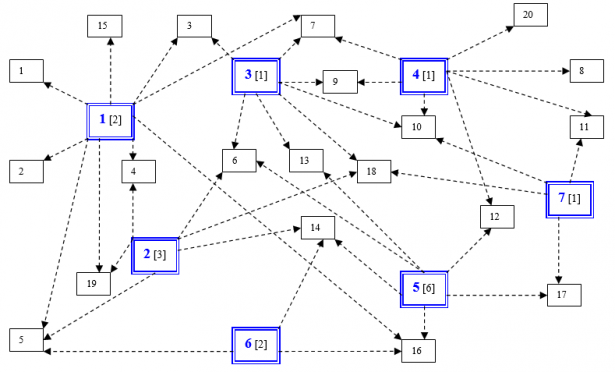
Per un problema così piccolo è facile fare subito delle semplificazioni. Innanzi tutto i vincoli p1, p2, p15, p20, p8 impongono che sia X1 = X4 = 1 in quanto sono gli unici magazzini possibili fornitori e pertanto debbono essere attivati. Stabilito questo i vincoli possono essere eliminati.
Possiamo poi eliminare i vincoli: p3, p4, p5, p7, p9, p10, p11, p12, p16, p19 che sono soddisfatti dalle posizioni X1 = X4 = 1 ed il vincolo p6 che risulta meno restrittivo del vincolo p13. In definitiva il problema può essere così riformulato:

X1 = X4 =1

p13) X3 + X5 >= 1
p14) X2 + X5 + X6 >= 1
p17) X5 + X7 >= 1
p18) X2 + X3 + X7 >= 1

Xi = 0 o 1 (i = 2, 3, 5, 6, 7)

F. Obiettivo: 3 + min {3X2 + X3 + 6X5 + 2X6 + X7}

Poiché i problemi di Programmazione lineare a numeri interi (ed a maggior ragione quelli di programmazione zero-uno) ammettono un numero finito di soluzioni si può pensare di risolverli in modo esaustivo, elencando cioè tutte le soluzioni possibili, scartando tutte quelle che non soddisfano i vincoli, calcolando la funzione obiettivo per le altre e, infine scegliendo la soluzione (ammissibile) che ottimizza il valore della funzione oggetto. Questa procedura è abbastanza lenta e fastidiosa per il problema originario (seppure non grandissimo) si devono infatti esaminare soluzioni però è istruttiva e fattibile per il problema ridotto cui siamo pervenuti: soluzioni. Un modo per elencare tutte le soluzioni possibili di un problema Zero-uno, senza dimenticarne alcuna, e quello di contare utilizzando la numerazione binaria. Questo è stato fatto nella tabella sottostante che elenca tutte le 32 soluzioni possibili, ammissibili e N0:





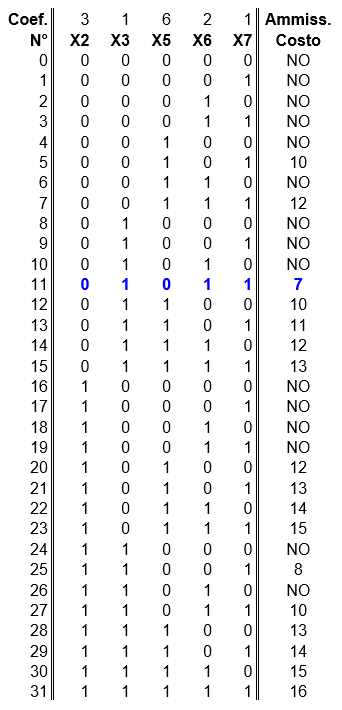
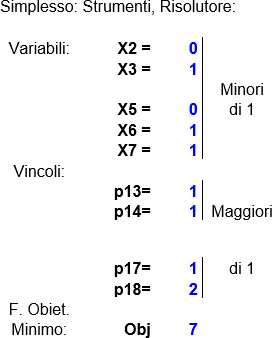
Guardando sopra si vede che, come previsto, il Risolutore Excel adottando il metodo del Simplesso, ha immediatamente trovato la soluzione in cui l'indicatore di costo è minimo (7) tra quelle ammissibili. Si osservi che tra i vincoli del problema non è stato necessario introdurre quello che le variabili siano intere (nello specifico o zero o uno). Ciò è stato possibile in quanto i coefficienti dei vincoli sono tutti unitari 1. Il metodo del Simplesso non consente da solo di trattare i vincoli di integralità delle variabili (nei casi in cui questi vincoli siano richiesti bisogna usarlo assieme al Branch and Bound che però ha complessità e tempi di convergenza superiori). Quindi questa proprietà (uni modularità della matrice dei vincoli), quando applicabile, è molto utile in quanto permette di ottenere rapidamente soluzioni a problemi a numeri interi che solitamente richiedono tempi di calcolo molto maggiori.

Conclusioni

La teoria della complessità computazionale ha posto un drastico solco tra problemi che hanno complessità polinomiali (facili) e problemi che hanno complessità esponenziale (molto difficili). Complessità polinomiale significa che i tempi di calcolo crescono, con la dimensione dei dati, con una funzione polinomiale. Complessità esponenziale significa che i tempi di calcolo crescono, con la dimensione dei dati, con una funzione esponenziale. E' evidente che la prima situazione è accettabile, la seconda è esplosiva anche per i più moderni supercomputer.
Oltre ai problemi/algoritmi che hanno complessità polinomiale (P) e a quelli che hanno una complessità esponenziale, esiste una classe intermedia di problemi/algoritmi (NP) per cui non è noto un algoritmo di soluzione in tempi polinomiali ma, se una soluzione ammissibile è conosciuta, si può verificare in tempi polinomiali se essa è ottima.
All'inizio del 1900 Hilbert aveva segnalato i problemi matematici da risolvere più importanti per il nuovo secolo: alcuni sono stati risolti altri no. All'inizio del 2000 questo elenco è stato aggiornato ed uno dei principali problemi ancora da risolvere è quello di stabilire se sia vero che: "P = NP"
Il problema è di grande rilevanza pratica oltre che teorica, tra l'altro è stato promesso un milione di dollari a chi riuscisse a risolverlo, perché se fosse dimostrato che anche per un solo problema NP hard (cioè i problemi NP difficili/completi) fosse trovato un algoritmo polinomiale allora si potrebbe inferire che tutti i problemi NP possono avere soluzioni in tempi polinomiali. Se la congettura, oggi ritenuta improbabile, P = NP fosse vera molti sistemi di crittografia e sicurezza informatica dovrebbero essere rivisti.
Veniamo, per concludere, al così detto "paradosso del Simplesso". L'algoritmo di Dantzig non è polinomiale, sono stati infatti costruiti dei casi che mostrano come il metodo finisca con lo spostarsi tra i vertici del poliedro convesso in maniera tale che i tempi di calcolo crescano esponenzialmente con il numero dei vertici da esplorare. Per la Programmazione lineare sono stati trovati, a partire dagli anni 70 dello scorso secolo, degli algoritmi basati sull'esame dei punti interni della regione ammissibile (Khacyan, Karmarkar,…) che sono polinomiali dunque in teoria molto più efficienti del Simplesso. Ebbene in pratica si è verificato che il Simplesso, per problemi non di grandissime dimensioni, è assolutamente concorrenziale con essi e spesso più rapido nella convergenza all'ottimo. Ciò dipende dal fatto che esso è si esponenziale nei casi peggiori (molto rari), ma nella grande maggioranza dei problemi converge rapidamente. Questo spiega perché molti software, tra cui il Risolutore Excel utilizzato in questo articolo, lo propongano all'interno dei loro sistemi per risolvere problemi di Programmazione lineare.

Riferimenti

• Il foglio elettronico come strumento per il Problem Solving, R. Chiappi, Franco Angeli, Milano 2008


• Project Management, Problem Solving, Decision Making, R Chiappi, Matematicamente.it 2015


• Programmazione matematica, di Hume e Smith.


• Problemi, Algoritmi e Codici, di Smith e Hume


• Piani di produzione, di Roberto Chiappi


• Allocazione degli investimenti di Roberto Chiappi


• Raffineria, di Roberto Chiappi


• Goal Programming: scelta dei titoli su cui investire, di Roberto Chiappi.

---

Note

1. Il lettore attento avrà notato che anche nel problema precedente le soluzioni sono intere, anche se non richiesto dalla natura del problema. Il motivo è dovuto al fatto che pure in questo caso la matrice dei coefficienti dei vincoli è uni modulare