Slitta

Luca e Piero sono grandi appassionati della montagna. Abili sciatori, sci-alpinisti, scalatori.
A inizio dell'inverno hanno convinto un amico a prestare loro una baita sulle Dolomiti. Non ci sono mai stati, ma dalla narrazione del proprietario capiscono che il luogo è incantevole: campi da sci, rocce, crepacci tra vette imponenti.
Si prendono una settimana di ferie e partono in auto per la vacanza. Il viaggio, lungo e faticoso ha richiesto due ore in più del previsto. Arrivano, piuttosto stanchi, al passo finale. Lasceranno l'auto, da dove raggiungeranno, in qualche modo, la baita. Decidono di affittare una slitta abbastanza capiente da trasportare tutto l'occorrente: attrezzatura da montagna, provviste per la settimana bianca, indumenti per quattro persone, libri. È stato programmato che la mattina seguente le loro ragazze arriveranno al passo e di lì scenderanno alla baita sciando.

I due amici entrano in un tipico caffè per riposarsi e fare una merenda calorica: strudel, paste, bevande calde. Dispongono sull'ampia tavola le carte della zona, con le mappe militari. E pianificano la tappa finale per raggiungere la baita. Intanto notano che il percorso dal passo alla baita è tutto in discesa e può essere ben approssimato da un arco di parabola.

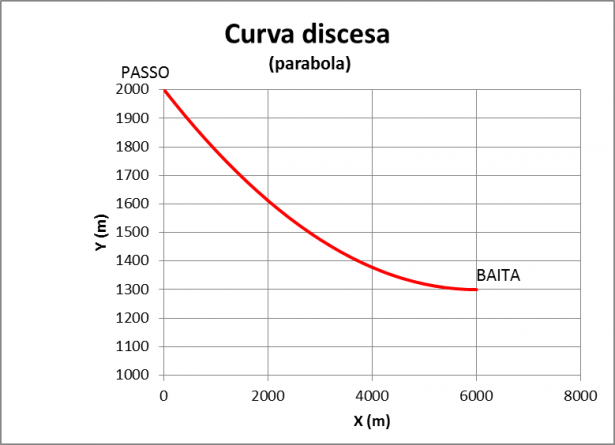
È una bella discesa innevata con un dislivello di 700 m. Come percorrerla?
Piero propone di scendere lentamente a zig-zag trattenendo la slitta con due funi: una persona davanti, l'altra dietro, per controllare la slitta che è piuttosto pesante con tutti i carichi. Luca nota che il tempo disponibile per la discesa è scarso dal momento che è pomeriggio inoltrato. Tuttavia i due amici hanno programmato di arrivare entro sera per accendere il camino e iniziare le pulizie della baita. In tal modo le loro ragazze, il mezzogiorno seguente, troveranno l'ambiente caldo e accogliente.

Occorre stimare quanto tempo ci vuole per la discesa. Allora Piero apre il suo inseparabile PC e cerca informazioni. Trova la correlazione del Metodo Svizzero, usato dai montanari, che lega il tempo di percorrenza in montagna alla distanza e al dislivello:

Si dovrebbe applicare il coefficiente

, essendo la marcia in discesa ma Luca nota che la marcia prevista dal metodo presumibilmente non si riferisce a terreno innevato, che certamente è più difficile. I due amici decidono di assumere , come dire che aumentano del 50% la durata prevista con .

Ora il dislivello è noto, mentre si non conosce la distanza da percorrere. Si potrebbe approssimarla con il segmento che unisce i punti di partenza e arrivo. Dal momento che si usa il metodo svizzero, Luca decide che si deve calcolare con precisione svizzera l'arco di parabola.

Piero ricorda a Luca che la lunghezza di un arco di curva si calcola con la nota formula:

[ \begin{equation}s=int_0^{xf} \sqrt{1+y'^2} , dx \tag{1}label{eq:1} end{equation} ]

che è una semplice applicazione del teorema di Pitagora in forma differenziale.

Ora la funzione parabolica

, in forma generale, è la seguente:

[ \begin{equation} y(x) = ax^2 + bx + c \tag{2}label{eq2} end{equation} ]

Mentre la sua derivata vale:

[ \begin{equation} y'(x) = 2ax + b \tag{3}label{eq3} end{equation} ]

La parabola che congiunge il passo e la baita ha i seguenti parametri:

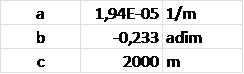
Quindi si ha:

[ \begin{equation} s=int_0^{xf} \sqrt{1+y'^2}, dx = int_0^{xf} \sqrt{1+(2ax+b)^2}, dx = int_0^{xf} \sqrt{Ax^2+Bx+C}, dx \tag{5}label{eq5} end{equation} ]

Dove

.

L'integrale deve essere calcolato tra il punto di partenza (

e quello di arrivo ().
L'integrale analitico, piuttosto complicato, è riportato in APPENDICE 2. Sostituendo costanti e parametri nella formula si ottiene il risultato: .

Piero applica ora la formula svizzera e ottiene

.
È questa una durata troppo lunga per il tempo disponibile, quindi la soluzione proposta non è accettabile.
Che fare? Luca propone allora di salire sulla slitta e di lanciarsi lungo la discesa: in breve si raggiungerebbe la baita. Per questo ci vogliono dei robusti teli, per avvolgere bagagli, attrezzature, merci, da bloccare alla slitta con delle corde elastiche. Questi materiali sono disponibili. Secondo Luca la cosa è fattibile. Piero, più riflessivo, si domanda se la discesa in slitta è sicura, anche perché con i due amici a bordo la massa totale raggiunge i 200 kg. Propone di fare un calcolo approssimato. Luca concorda, prende un block-notes e comincia a scrivere il modello del moto della slitta. Le forze in gioco sono la gravità (), la resistenza di attrito radente () nel moto della slitta che striscia sulla neve, la reazione normale ((F)_n) della pista sulla slitta, come appare in figura sotto. Mentre V è il vettore velocità.

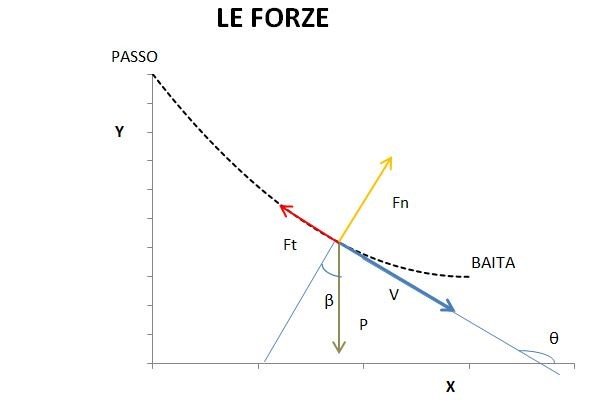
La slitta è rappresentata da un punto materiale vincolato a percorrere la parabola. Di conseguenza la velocità della slitta è sempre tangente alla parabola. Questo vuol dire che in ogni istante la forza normale (i.e. perpendicolare) che la pista esercita sulla slitta (uguale e contraria alla forza normale che la slitta esercita sulla pista) è bilanciata dalla componente della forza di gravità normale alla parabola:

[ F_n = Pcos(\beta) = mgcos(\beta) ]

La forza di attrito radente esercitato dalla neve sulla slitta è una forza tangenziale con direzione contraria al vettore velocita

. Per la legge empirica di Coulomb è proporzionale alla forza normale:

( F_t = mu_d F_n = mu_d mgcos(\beta) ,,,,,, (mu_d = 0.15 ,, \text{ è il coeff. di attrito radente dinamico}) )

Luca comincia a scrivere le equazioni del moto, usando la seconda legge di Newton ma Piero lo ferma osservando che con questo procedimento si otterrà un'equazione differenziale di 2° grado lungo la tangente alla parabola, riconducibile a due equazioni di primo grado. Un po' complesso. Meglio sarebbe fare un bilancio di energia. Luca concorda.

Luca scrive che il lavoro infinitesimo esercitato dalla forza di attrito vale: (dL_t = F_t ds)

Dove

è l'arco infinitesimo di parabola, che a meno di infinitesimi di ordine superiore, coincide con il vettore spostamento lungo la direzione della velocità.

Risulta:

( dL_t = F_t ds = mu_d mgcos(\beta)ds )

Ora Piero ricorda a Luca che la lunghezza di arco è definita dalla (eqref{eq:1}) scritta in forma differenziale
(gli studenti della secondaria superiore sanno che la derivata di un integrale coincide con la funzione integranda):

( dL_t = F_t ds = mu_d mgcos(\beta)ds = mu_d mgcos(\beta)\sqrt{1+y'^2}dx )

Per la definizione di derivata sappiamo che (y'=\tan(\theta))

Allora ( dL_t = mu_d mgcos(\beta)\sqrt{1+\tan(\theta)^2}dx )

La figura precedente che schematizza le forze riporta due angoli β e θ. Come si vede facilmente risulta:

( \beta = pi - \theta mbox{ e quindi } cos(\beta) = -cos(\theta)). Ne consegue: ( dL_t = -mu_d mgcos(\theta)\sqrt{1+\tan(\theta)^2}, dx)

Infine Luca rammenta a Piero che dalla trigonometria si sa che ( cos(\theta) = frac{1}{\sqrt{1+\tan(\theta)^2}} ).

E la formula precedente si semplifica:

( dL_t = -mu_d mgdx)

dove il segno negativo sta a indicare che si tratta di lavoro negativo, in quanto lo spostamento si oppone alla forza di attrito radente.

"Ci interessa il valore assoluto del lavoro", dice Piero, quindi Luca scrive: (dL_t = mu_d mgdx).

Che integra ottenendo: ( L_t = mu_d mgx ).

A questo punto si può scrivere il bilancio di energia meccanica (somma di energia cinetica e potenziale): la differenza di energia meccanica tra la partenza (dove

) e il generico punto di ascissa x eguaglia il lavoro della forza di attrito.

, vale a dire:

[ \begin{equation} (mgy_0 + frac{1}{2}mv_0^2)-(mgy+frac{1}{2}mv^2)=mu_d mgx \tag{6}label{eq:6} end{equation} ]

Il significato della (eqref{eq:6}) è il seguente: la perdita di energia meccanica è dovuta al lavoro di attrito. Questo lavoro si traduce in una trasformazione (degradazione) dell'energia meccanica in calore che va ad aumentare l'energia interna del sistema slitta-neve-aria.
"Se assumiamo che la velocità iniziale

sia nulla", dice Piero," l'equazione si semplifica e si risolve rispetto a ":

[ \begin{equation} v = \sqrt{2g(y_0-y-mu_d x)} \tag{7} label{eq:7} end{equation} ]

La (eqref{eq:7}) permette dunque a Luca di determinare l'andamento della velocità in funzione di x.

Luca prova ora ad azzerare la (eqref{eq:7}) per determinare il valore di x che per il quale la slitta si ferma (

). E ottiene:

[ \begin{equation} x_{mbox{stop}} = frac{y_0-y(x)}{mu_d}\tag{8}label{eq:8}end{equation}]

dove

è l'equazione della parabola (eqref{eq2}).

La (eqref{eq:8}) è una semplice equazione di 2° grado che, volendo, si può anche risolvere per sostituzioni successive partendo da un valore x di tentativo. Luca inserisce i valori e dopo alcune iterazioni ottiene (x_{mbox{stop}}=4286 m).

Ma la baita ha per ascissa

, quindi la slitta non ce la fa ad arrivare fino alla baita e si ferma un paio di chilometri prima. Questo risultato pare davvero strano a Luca: si aspettava che una volta partita la slitta continuasse a scivolare fino alla baita, trascinata dalla componente della forza di gravità tangente alla pista. Perché questo non avviene? Piero spiega a Luca che, man mano che la slitta scende lungo la pista, la sua inclinazione (vale a dire la tangente) si riduce. In questo modo aumenta la reazione normale e quindi la forza di attrito. Questa frena sempre più la slitta fino alla fermata completa. Luca ha capito e tuttavia replica che è comunque possibile completare la discesa trascinando la slitta per il tratto che manca. Piero sembra d'accordo, ma propone di tracciare l'andamento della velocità con la (eqref{eq:7}). Qui sotto il diagramma di Piero:

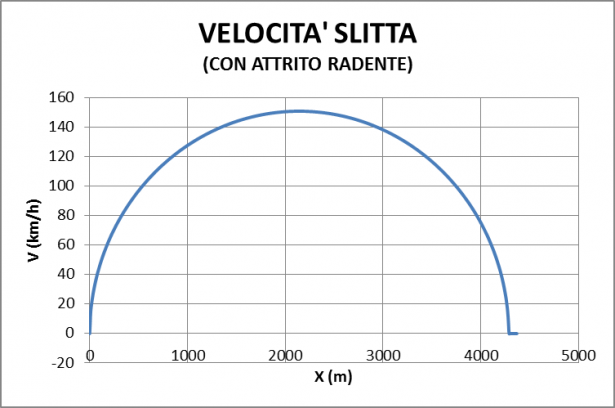
Si vede che la slitta accelera fino a raggiungere una velocità massima, poi rallenta fino a fermarsi.
I due amici notano, allarmati, che la slitta raggiungerà 150 km/h, una velocità eccessiva e molto pericolosa per la slitta. Controllare la slitta in discesa a queste velocità non è facile né consigliabile. Ora Piero ha un dubbio: forse il modello che hanno scritto è poco realistico. A tale velocità di sicuro la slitta sarà frenata dall'aria.
Luca passa il foglio a Piero, più esperto di aerodinamica, il quale scrive l'espressione della resistenza aerodinamica dell'aria sulla slitta:

[ F_a = frac{1}{2} C_x \rho_a Sv^2 ]

Questa resistenza è un vettore contrario alla velocità v, che si somma alla resistenza di attrito radente.

Il lavoro di questa forza è dato da:

(dL_a = F_a ds = F_a \sqrt{1+y'^2} )

oppure, in forma integrata:

( L_a = int F_a,ds = int F_a\sqrt{1+y'^2}, dx )

Piero riprende il modello (eqref{eq:6}) aggiungendo il lavoro della resistenza aerodinamica:

( (mgy_0+frac{1}{2}mv_0^2)-(mgy+frac{1}{2}mv^2)= )

( mu_d mgx + frac{1}{2}C_x\rho_a S int v^2\sqrt{1+y'^2}, dx \tag{9}label{eq:9} )

Ora la faccenda diventa complicata perché la variabile dipendente (la velocità v ) appare sotto il segno d'integrale: non si riesce a risolvere l'equazione algebrica rispetto a v, che è funzione di x. La (eqref{eq:9}) è un'equazione integrale.

Ecco allora che Luca ha un'idea: provare a passare alla forma differenziale. Luca sa che data una funzione generica

, il suo differenziale vale

[ dy=f'(x)dx ]

Luca riprende l'equazione (eqref{eq:6}) e riscrive il membro di sinistra:

((mgy_0+frac{1}{2}mv_0^2) -(mgy+frac{1}{2}m^2))

Ne calcola il differenziale:

Il primo termine tra parentesi è una costante e il suo differenziale è zero. Il secondo termine diventa: ( -(mgdy+mvdv) ).

Mentre, per scrivere il membro di destra dell'equazione differenziale, basta inserire le espressioni differenziali dei due lavori che Luca ha scritto prima. Si ottiene complessivamente:

[ \begin{equation} -(mgdy+mvdv) = mu_d mgdx + frac{1}{2}C_x\rho_aSv^2\sqrt{1+y'^2}\tag{10}label{eq:10} end{equation}]

Inoltre ( dy=y'dx=(2ax+b)dx ) che può essere introdotta nella (eqref{eq:10}) ottenendo:

[ \begin{equation} mvdv = -Big[ mg(2ax+b)+mu_d mg + frac{1}{2}C_x \rho_a Sv^2\sqrt{1+(2ax+b)^2} Big]dx \tag{11}label{eq:11} end{equation} ]

E quindi:

( frac{dv}{dx} = -frac{1}{mv} Big[mg(2ax+b)+ mu_d mg + frac{1}{2} C_x \rho_a Sv^2 \sqrt{1+(2ax+b)^2} Big])

È questa un'equazione differenziale del 1° ordine in forma normale, del tipo:

[ frac{dv}{dx}=f(x,v)]

Che deve essere risolta rispetto alla variabile v, con metodi numerici. Ma c'è un problema. Nel punto iniziale (

) la velocità è nulla e la funzione ha valore infinito. "C'è un punto di discontinuità che mette in crisi il calcolo numerico", dice Luca.

Piero propone allora un espediente: far sparire il termine v a denominatore nel secondo membro.

"Basta portarlo al membro di sinistra", dice:

( 2vfrac{dv}{dx}=frac{dv^2}{dx} =-frac{2}{m} Big[ mg(2ax+b)+ mu_d mg + frac{1}{2} C_x\rho_aSv^2 \sqrt{1+(2ax+b)^2}Big] )

In questo modo l'equazione differenziale è del tipo:

[ frac{dv^2}{dx} = f(x,v^2) ]

Che si risolve rispetto alla variabile

. Compare anche la variabile y, che è funzione nota di x (la parabola del percorso).
Per integrarla si può usare Runge-Kutta, routine d'integrazione che Piero ha nel PC. Per applicarla occorre scrivere un pezzo di codice per il problema specifico, fare il debugging e risolvere. Ma ormai è tardi e il tempo stringe. Si decide allora di usare il vecchio metodo di Eulero (vedere RIFERIMENTI), piuttosto impreciso. "Vada per Eulero", dice Piero, "basta prendere un passo d'integrazione Δx molto piccolo".

E scrive il modello finale:

[ \begin{equation} frac{Delta v^2}{Delta x} = - frac{2}{m} Big[ mg(2ax+b)+mu_d mg + frac{1}{2} C_x\rho_a Sv^2 \sqrt{1+(2ax+b)^2}Big] \tag{12}label{eq:12} end{equation} ]

Ora, per definizione:

[ Delta v^2 = v_{i+1}^2 - v_i^2 ]

E la (eqref{eq:12}) diventa:

[ \begin{equation} v_{i+1}^2 = v_i^2 - frac{2}{m} Big[ mg(2ax_i + b)+ mu_d mg + frac{1}{2} C_x\rho_a Sv_i^2 \sqrt{1+(2ax_i + b)^2} Big] \tag{13}label{eq:13}end{equation} ]

"Questo semplice algoritmo ricorsivo si risolve in un attimo con Excel!", dice Piero.
La condizione iniziale è, ovviamente: per

Piero fa i calcoli con il PC è ottiene la soluzione numerica, come da diagramma seguente:

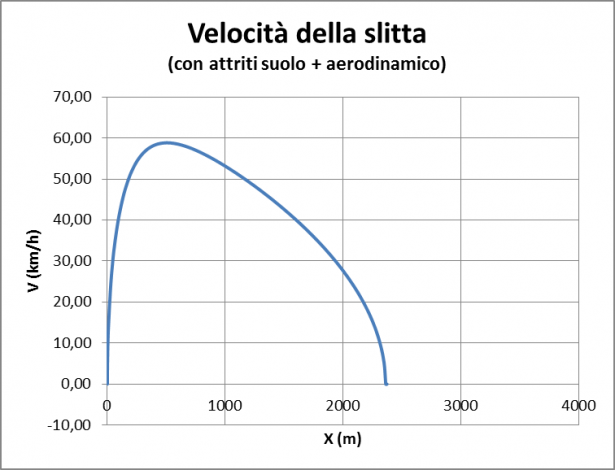
Questa soluzione è ben diversa da quella del modello precedente. Evidentemente la resistenza aerodinamica ha giocato un ruolo importante. La velocità massima è inferiore a 60 km/h che, ai due amici abili sciatori, pare accettabile. La slitta si ferma a

, dopo pochi minuti. Resta poi da trascinare la slitta per quasi 4 km per raggiungere la baita. Usando il metodo svizzero si calcola che ci vogliono altri 93 minuti. Purtroppo si è fatto tardi è fra un'ora cala l'oscurità. I due amici capiscono che oggi dovranno rinunciare. Dormiranno in albergo al passo per raggiungere la baita domattina.

Un anziano valligiano, seduto al tavolo vicino, ha ascoltato con curiosità l'intera conversazione e, ridendo tra sé, scuote la testa. Per lui, esperto del luogo, era evidente che la discesa dei due amici doveva essere rimandata al giorno successivo. Mentre sorseggia con studiata lentezza un delizioso punch, riprende a leggere placidamente il suo libro di astrofisica. Nella sala si diffonde il profumo dello strudel, appena sfornato per una allegra comitiva di sciatori. Cala il tramonto dietro i monti innevati.

CONCLUSIONE

Il piccolo problema di meccanica descritto nell'articolo è stato affrontato dai due amici - che comprendiamo esser amanti delle scienze dure - in due modi, in termini di bilancio di energia meccanica.
Il primo ha portato a scrivere un modello di tipo algebrico, molto semplice da risolvere. Purtroppo è risultato poco realistico ed è stato messo da parte.
Il secondo ha prodotto un'equazione differenziale, non risolvibile in forma chiusa. È stata integrata per via numerica con il metodo di Eulero (sommo matematico e meccanico).
Tutti i calcoli sono riportati nel file Excel allegato all'articolo.

APPENDICE 1

Il metodo ha tuttavia un lieve difetto: non ha fornito la durata della discesa in slitta. Nel nostro caso la cosa aveva ben poca importanza perché era evidente che alle velocità calcolate la durata era di pochi minuti, mentre il tempo di marcia a piedi, per completare la discesa, richiedeva più di un'ora. Tuttavia, se vogliamo essere precisi (come gli svizzeri), possiamo calcolare facilmente la durata della discesa sulla slitta. Sappiamo che per definizione:

[ v = frac{ds}{dt}]

Ed anche che:

[ ds = \sqrt{1+y'^2}, dx ]

Dunque: ( dt = frac{ds}{v} = frac{\sqrt{1+y'^2}}{v}, dx )

Ora sappiamo che

mentre è nota essendo stata calcolata numericamente con la (eqref{eq:13}).

Non resta allora che calcolare un semplice integrale per via numerica - ad esempio come somma di trapezi - per ottenere:

[ T=int_0^{x_{mbox{stop}}} frac{\sqrt{1+(2ax+b)^2}}{v(x)}, dx = mbox{4 minuti} ]

APPENDICE 2

Lunghezza di un arco di parabola

( int_0^L \sqrt{Ax^2+Bx+C}, dx = frac{(4AC-B^2)ln[2\sqrt{A}\sqrt{AL^2+BL+C}+2AL+B]}{8A^{1.5}} +)

( frac{(B^2-4AC)ln[2\sqrt{AC}+B]}{8A^{1.5}}+ frac{(2AL+B)\sqrt{AL^2+BL+C}-B\sqrt{C}}{4A} )

RIFERIMENTI

• https://it.wikipedia.org/wiki/Attrito#Attrito_radente (attrito radente)
• https://it.wikipedia.org/wiki/Energia_meccanica (energia meccanica)
• https://it.wikipedia.org/wiki/Metodo_di_Eulero (metodo di Eulero)
• http://www.girovagando.net/info_utili/tempi.html (metodo svizzero)
• https://it.wikipedia.org/wiki/Regola_del_trapezio (integrazione con regola trapezio)
• https://it.wikipedia.org/wiki/Aerodinamica#Collegamenti_esterni (attrito aerodinamico)