La più grande soddisfazione non è la conoscenza, ma il processo dell'apprendimento [Gauss]

"La più grande soddisfazione non è la conoscenza, ma il processo dell'apprendimento, non il possesso del sapere ma il processo per raggiungerlo". Carl Gauss (1777, 1855)

Il maestro aveva dato ai ragazzi (di circa 9 anni) un problema: sommare tutti i numeri da 1 a 60 invitandoli a portargli la soluzione non appena avessero la avessero calcolata. Pochi minuti dopo il piccolo Carl salta su, corre al tavolo e consegna la soluzione: 1+2+...+59 + 60 = 1830.

Come mai? Come ha fatto il monello? Sapeva già a memoria la soluzione?

Quando, dopo molto tempo, tutti avevano consegnato il compito, Carl, interrogato dal maestro su come avesse fatto, disse con semplicità di aver scritto mentalmente uno sotto l'altro il numero più alto e il numero più basso, poi il successivo più alto e il successivo più basso, e così via sino al termine, calcolando infine i totali di tutte le coppie che valevano sempre 61:
basso: 1 2 3 ... 29 30
alto: 60 59 58 ... 32 31
Totale: 61 61 61 ...61 61

moltiplicare a mente 30x61 era poi stato facile poiché: 3x6 = 18 quindi 61x3 = 183 e 183x10 = 1830.

In generale la formula per sommare i primi n numeri naturali (caso particolare di progressione aritmetica) è:

Il Princeps Mathematicorum, come poi venne chiamato, divenne anche un campione oltre che della matematica pura anche di quella applicata ed in special modo della geodesia, della fisica e dell'astronomia.

Gauss, le cui capacità di calcolo ricordano nel passato quelle di Archimede e nel futuro quelle di Von Neumann, non aveva alcun bisogno di aiuti esterni per calcolare le cose più difficoltose e complicate: i sistemi di equazioni lineari, le equazioni di grado n-esimo (a lui è dovuto il teorema fondamentale dell'algebra), i numeri e le variabili complesse, gli spazi curvi, gli integrali, le congruenze, le distribuzioni di probabilità, ecc.

Scoprì prima di ogni altro le geometrie non euclidee, ma non pubblicò nulla nel timore, come lui stesso disse, di suscitare le strida dei beoti.

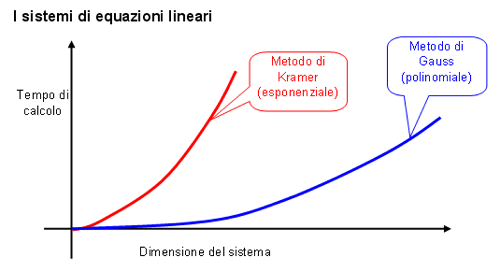
Disporre di algoritmi efficienti per risolvere i sistemi di equazioni lineari è fondamentale per affrontare problemi tecnici, economici, aziendali, di ricerca pura e di ricerca applicata. Ancora oggi nelle scuole molti insegnano il metodo di Cramer senza ricordare che la sua validità è puramente didattica e che l'applicabilità pratica è ridotta ai sistemi che abbiano meno di 10 equazioni in 10 incognite. Se programmassimo l'algoritmo di Cramer e quello di Gauss su un calcolatore in grado di eseguire un milione di operazioni significative (moltiplicazioni e divisioni) al secondo, il metodo di Cramer impiegherebbe più di un milione e mezzo di anni per risolvere un sistema di sole 20 equazioni in 20 incognite, mentre il metodo di Gauss impiegherebbe circa un centesimo di secondo. Se poi il sistema è costituito da 50 equazioni il tempo trascorso dall'origine dell'universo ad oggi non sarebbe sufficiente per calcolare la soluzione col metodo di Cramer (né in tempo utile concluderebbe l'operazione un computer capace di 1000 miliardi di operazioni al secondo), mentre il metodo di Gauss fornirebbe il risultato in meno di due decimi di secondo.

Gli errori di misura piccoli (sia positivi che negativi) sono più probabili degli errori di misura elevati; questa considerazione porta alla curva di distribuzione di Gauss (curva normale o curva a campana per la prima volta descritta da de Moivre nel 1733). La distribuzione di Gauss gode di una importante proprietà (teorema del limite centrale): se si ha un fenomeno casuale che dipende dalla somma di più variabili casuali (in genere ne bastano 10 o 12) allora il fenomeno totale ha una distribuzione di probabilità che tende alla curva di Gauss al crescere del numero delle variabili e indipendentemente dalla forma delle distribuzioni componenti.

In natura moltissime grandezze (dall'altezza delle persone, alla velocità delle molecole nei gas, al quoziente intellettivo, ecc.) seguono una curva di Gauss. Le curve a campana, che hanno degli asintoti che precipitano esponenzialmente verso lo zero, ci sono familiari e tendiamo ad usarle spesso, magari a sproposito come nella stima delle variazioni di prezzo dei titoli di borsa.

Negli ultimi anni B. Mandelbrot ed altri hanno mostrato che in finanza, come in altri sistemi complessi, gli eventi casuali non seguono le curve di Gauss, ma delle leggi di potenza che decrescono molto più lentamente dando luogo a degli eventi rari, i famosi cigni neri, molto più frequenti di quanto previsto con la curva normale di Gauss.

Se si hanno diverse osservazioni di uno stesso fenomeno, il valore x che minimizza i quadrati degli scarti delle varie osservazioni è dato dalla media aritmetica delle osservazioni stesse. Il metodo dei minimi quadrati consente di costruire rette e curve utili per interpolare ed extrapolare dai dati disponibili funzioni incognite.

La curva di Gauss ed il metodo dei minimi quadrati sono tra gli strumenti statistici e di calcolo delle probabilità più utilizzati per risolvere i problemi aziendali: dalla produzione al marketing, dalla qualità all'analisi del rischio, dall'analisi delle serie storiche alla pianificazione strategica.

"Come esprimerle la mia ammirazione e il mio stupore nel vedere il mio stimato corrispondente signor Le Blanc trasformarsi in un personaggio che dà un esempio così luminoso di ciò che io stenterei a credere. Il gusto per le scienze astratte, in generale, e per i misteri dei numeri, in particolare, e rarissimo: ma non è questo il motivo del mio stupore. Il fascino incantevole di questa scienza sublime si rivela solo a coloro che hanno il coraggio di immergersi nel suo studio. Ma quando una persona del sesso che, secondo i nostri costumi e pregiudizi, deve incontrare difficoltà infinitamente superiori a quelle degli uomini nel familiarizzare con queste scabrose ricerche, riesce nondimeno a sormontare gli ostacoli e a penetrare le parti più oscure della materia, allora senza dubbio ella deve possedere il coraggio più elevato, talenti straordinari e un genio superiore. Niente potrebbe in maniera altrettanto lusinghiera e inequivocabile fornirmi la prova che le attrattive di questa scienza, che ha arricchito la mia vita di gioie così numerose, non sono chimere quanto la predilezione di cui voi l'avete onorata." Lettera di Gauss alla matematica Sophie Germain.

Sophie Germain ebbe intense corrispondenze scientifiche con i maggiori matematici del suo tempo tra cui Lagrange, Legendre e Gauss, ma temendo di creare imbarazzo nei suoi corrispondenti, i quali avrebbero guardato con sospetto una "donna matematica", aveva creato il suo pseudonimo maschile: Monsieur Le Blanc. Le sue lettere ricche di problemi risolti ed idee feconde sulla teoria dei numeri, le avevano fatto subito guadagnare la stima del grande Gauss. Nel 1837, in occasione della celebrazione dei cento anni dell'università di Gottinga Gauss ricordava con rammarico Sophie Germain, ormai defunta, e dichiarava: "Ella ha dimostrato che anche una donna può realizzare qualcosa d'importante nella più rigorosa ed astratta delle scienze e per questa ragione avrebbe meritato una laurea ad honorem". L'aver riconosciuto le capacità di avere idee feconde e risolvere problemi da parte della metà della popolazione le cui capacità intellettuali erano all'epoca sistematicamente sottovalutate, fu certamente uno dei tanti meriti di Carl Friedrich Gauss.