Villetta

PREMESSA

Lisa è davvero soddisfatta. Da un anno si è comprata una villetta in collina. Dotata di un'ampia porta-finestra che copre gran parte della facciata sud. Con una bella vista sulla pianura e sul fiume che s'intravede all'orizzonte.
Ma non tutto è perfetto. La costruzione risale a più di quarant'anni fa, quando ancora le tecniche e le normative per il risparmio energetico erano ben poco sviluppate. Di conseguenza nella stagione fredda la villetta ha importanti dispersioni che si traducono in spese per il riscaldamento piuttosto salate. Lisa è diventata piuttosto attenta a limitare i consumi.
Come detto l'edificio è piuttosto vecchio e l'impianto di riscaldamento è davvero antiquato: una scomoda stufa a legna/carbone, dal momento che non esiste una rete pubblica per il trasporto del gas.
In una bella giornata invernale, verso le undici, Lisa decide di assentarsi per quattro ore. In previsione di questo al mattino non ha caricato il combustibile; in tal modo, di fatto, il riscaldamento è spento. Lisa pensa che la casa non si raffredderà. Anzi confida che l'irraggiamento solare attraverso la vetrata possa compensare le dispersioni termiche.
Ci domandiamo se il suo ottimismo sia fondato.

MODELLO

Per far questo possiamo immaginare di sviluppare un piccolo modello matematico che rappresenti il fenomeno. La figura sotto rappresenta la villetta, in modo molto semplificato, come un parallelepipedo; supponiamo inoltre che si tratti di un grande monolocale, il che vuol dire che non esistono pareti interne. La figura riporta i flussi termici in entrata e uscita.

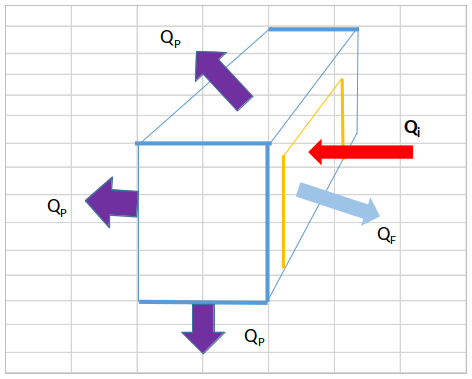
Notiamo che esiste un'importante dispersione

attraverso le pareti (inclusi i solai di pavimento e tetto), un'altra dispersione attraverso la grande vetrata sul lato sud. Nella vetrata entra il flusso termico causato dall'irraggiamento solare.
Questi tre flussi, inseriti in un bilancio termico, ci permettono di calcolare la temperatura all'interno della casa. Vediamo di scrivere le espressioni che definiscono i tre flussi. Si ha:

Dove i due flussi termici in uscita sono definiti come prodotto di tre termini: una costante

(trasmittanza), la differenza di temperatura tra l'interno e l'ambiente, la superficie di scambio di questi flussi.
Abbiamo in tal modo introdotto la trasmittanza che, come appare evidente dalle formule sopra riportate, rappresenta la quantità di calore che in un secondo attraversa di parete (di qualsiasi tipo) quando la differenza di temperatura tra i due lati della parete è di 1°C.
Ovviamente in un caso reale pavimento, soffitto (i.e. tetto), pareti sono fatte di materiali diversi e hanno trasmittanze diverse. In questo modello semplificato si è immaginato che siano uguali.

Per spiegare il termine del flusso in entrata (

) vediamo la figura sotto

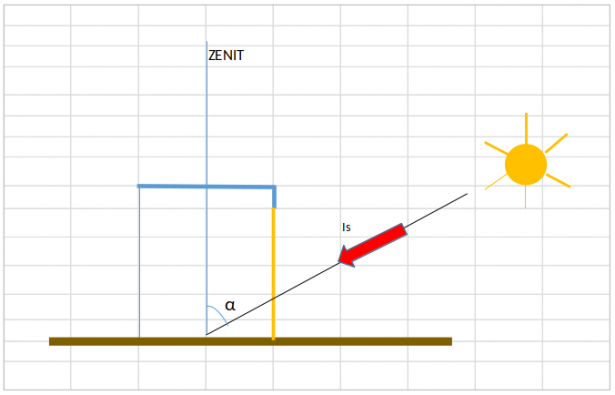
I raggi del sole arrivano sulla terra con un angolo di zenitale α (che dipende dalla latitudine, dalla stagione e dall'ora del giorno). I raggi trasportano la potenza termica specifica

(espressa in , che rappresentiamo con un vettore). Tale vettore si può scomporre nelle due direzioni orizzontale e verticale. La componente verticale finisce sul terreno, dove è dispersa. La componente orizzontale, , colpisce la vetrata. Una sua frazione () è riflessa. La parte che entra vale: .
Moltiplicando tale grandezza per la superficie della finestra si ottiene la potenza entrante (in ).
Ora ci chiediamo che tipo di bilancio termico vogliamo fare.
Supponiamo di voler calcolare la condizione di equilibrio termodinamico, che di sicuro si raggiungerebbe se i flussi termici rimanessero stabili per un tempo molto lungo.

BILANCIO TERMICO ALL'EQUILIBRIO

Eguagliando la potenza entrante a quella uscente:

[ Q_i = Q_p + Q_f ]

Vale a dire:

[ \begin{equation}I_s (1 -F_r) \sin(alpha) S_f = U_p (T_i - T_e) S_p + U_f (T_i - T_e) S_f \tag{1}label{eq1} end{equation} ]

Che si risolve rispetto a

:

[ \begin{equation}T_{i,eq} = T_e + frac{I_s (1 -F_r) \sin(alpha) S_f }{U_p S_p + U_f S_f} \tag{2}label{eq2} end{equation} ]

Come detto la temperatura di equilibrio rappresenta un valore limite che si raggiungerebbe, a condizioni di flussi costanti, in un tempo infinito. Ci dà un'indicazione importante, ma non spiega cosa succede nell'intervallo limitato di qualche ora.

TRANSITORIO TERMICO

Per far questo è necessario un modello che renda conto dell'evoluzione temporale della temperatura interna. Notiamo che durante il transitorio termico verso l'equilibrio, la villetta si può riscaldare (o raffreddare). Questo avviene attraverso un accumulo (o perdita) di energia da parte della casa.
Ora l'energia (entalpia) accumulata si esprime come prodotto della massa per il calore specifico () di tale massa, per la temperatura. Assumiamo, in modo approssimato, che la massa della casa sia rappresentata dalla massa delle sue pareti . In tal modo l'entalpia è data da .

Scriviamo ora il bilancio termico in forma differenziale, vale a dire riferito a quantità infinitesime:

( M_p C_p dT_i = [I_s (1-F_r)cos(alpha)S_f - U_p(T_i-T_e)S_p - U_f(T_i-T_e)S_f]dt )

( = {I_s(1-F_r)\sin(alpha)S_f - [U_pS_p+U_fS_f](T_i-T_e)}dt)

E dunque:
[ frac{dT_i}{I_s(1-F_r)\sin(alpha)S_f-[U_pS_p+U_fS_f](T_i-T_e)}=frac{dt}{M_pC_p} ]

Raggruppando le costanti si scrive in forma più semplice:

[ \begin{equation}frac{dT_i}{BT_i - A} = - frac{dt}{M_p C_p} \tag{3}label{eq3} end{equation} ]

dove:

( A = I_s (1-F_r)\sin(alpha)S_f + [U_pS_p + U_fS_f]T_e )

( B = U_p S_p + U_f S_f )

In definitiva abbiamo trasformato l'equazione differenziale, tramite separazione delle variabili, in due integrali, che facilmente risolviamo con la condizione iniziale: (t = 0, T_i = T_{i_0})

( int_{T_{i_0}}^{T_i} frac{dT_i}{BT_i-A} = - int_0^t frac{dt}{M_pC_p} )

che diventa:

( frac{1}{B} ln Big(frac{BT_i -A}{BT_{i_0}-A}Big) = - frac{t}{M_pC_p})

Ora si prende l'esponenziale di ambo i membri e si risolve rispetto a

:

[ \begin{equation}T_i = frac{A}{B} + Big(T_{i_0} - frac{A}{B} Big)expBig(-frac{Bt}{M_pC_p}Big) \tag{4}label{eq4} end{equation} ]

La ((\ref{eq4})) è una funzione esponenziale che ha i seguenti estremi:

( t = 0 \rightarrow T_i = T_{i_0} )

( t \rightarrow +infty \rightarrow T_i = T_e + frac{I_s (1-F_r)\sin(alpha)S_f}{U_pS_p+U_fS_f} )

Notiamo che per

si ritrova, ovviamente, il valore iniziale. Mentre il limite all'infinito individua la condizione di equilibrio termodinamico ((\ref{eq2})) che abbiamo visto.

Il file EXCEL allegato all'articolo riporta costanti e parametri e calcoli del modello nello Sheet Modello1.
Data la temperatura iniziale (T_{i_0} = 22 °C) e quella esterna

, la temperatura di equilibrio - calcolata con la ((\ref{eq2})) - risulta essere (T_{i, eq} = 25{,}1 °C), quindi si avrà un lieve aumento della temperatura interna.

Il diagramma conclusivo riporta l'andamento della temperatura in funzione del tempo, ottenibile dalla ((\ref{eq4})).

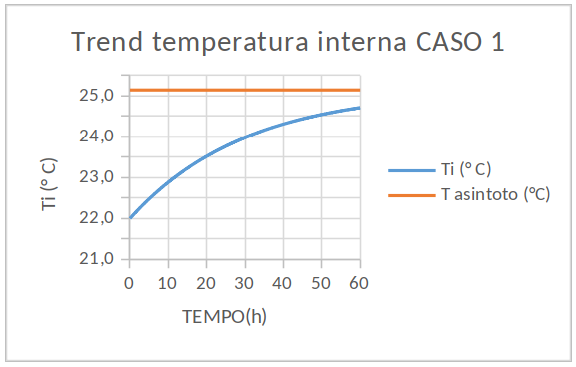
Si osserva che occorrerebbero alcune decine di ore per avvicinarsi alla (T_{i, eq}). Tuttavia l'insolazione diurna non dura così a lungo. E dopo quattro ore di assenza da casa la

è aumentata di soli 0,4 °C. In definitiva, pur in assenza di riscaldamento, non si è raffreddata. Dunque Lisa aveva ragione (Ovviamente questi calcoli sono basati su costanti e parametri ipotizzati nel file EXCEL).

CASO 2

Potremmo chiederci, per semplice curiosità, quale sarebbe stato l'andamento della temperatura interna nel caso in cui al posto di una vera e propria casa in muratura, si fosse trattato di una baracca, oppure di una serra, a pari geometria e trasmittanze. In questo caso particolare potremmo assumere che lo spessore delle pareti e la loro massa siano trascurabili. E dunque l'unica cosa che si scalda o raffredda all'interno dell'edificio sarebbe l'aria. Rifacendo i calcoli riferiti all'aria interna (massa pari a circa 500 kg) il transitorio termico è ben differente (vedere Sheet Modello 2). La raggiunge l'equilibrio in circa un'ora, come appare dal seguente diagramma.

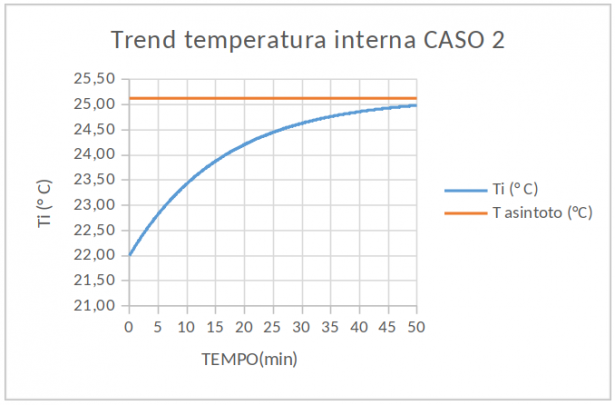
CONCLUSIONE

Scopo di quest'articolo è stato di familiarizzare il lettore con le grandezze, i criteri, i parametri principali che entrano in gioco nel calcolo dei flussi termici di un edificio. Mostrare le equazioni importanti che si applicano. E provare a risolvere, in forma semplificata, un paio di casi.
Chi è interessato all'argomento può provare a usare i modelli cambiando i valori di costanti e parametri. Nel caso di un edificio di recente costruzione le trasmittanze sono molto inferiori, anche dimezzate.
E si può anche assumere , per valutare il raffreddamento in assenza dell'insolazione.

Ovviamente il calcolo - di progetto o verifica - richiederebbe modelli molto più complessi e dettagliati, sulla base di metodi, normative, manuali…. e molta esperienza. Cosa che ben volentieri lasciamo agli esperti.

RIFERIMENTI

• http://www.solaritaly.enea.it/Documentazione/Archivio%20Radiazione%20e%20Solaritaly.pdf;
• http://www.diee.unica.it/~pisano/13_143_20080930104402.pdf;
• http://oldsite.ing.unisalento.it/seo-start/page/home.bacheca_allegato/news_id/7381fcd9718ecff58049234fdd275964/no_header/seo-stop/index.php?format=.pdf.