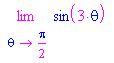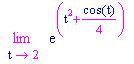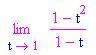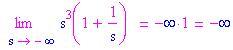Limiti di funzioni e funzioni continue
Se il valore di una funzione f(x) si avvicina al valore L quando x si avvicina ad a , diciamo che f(x) ha come limite L per x tendente ad a.Noi scriviamo ciò, in notazione matematica, così:
Tale notazione matematica si legge nel seguente modo: il limite di f(x) per x che tende ad a equivale a L, dove f(x) è una funzione, x è la variabile indipendente della funzione f(x), a è un numero che corrisponde al valore a cui tende la x mentre L è il valore della funzione quando le ascisse tendono ad a.
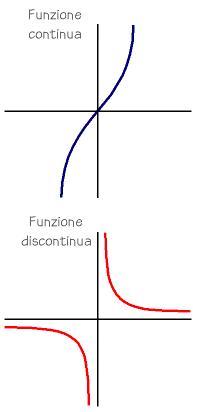
In seguito riportiamo due esempi di una funzione continua e di una discontinua.
Affinchè f(x) abbia limite L quando x si avvicina ad a, devono esistere il limite destro e il limite sinistro per x tendente ad a e devono essere uguali.
Ricordiamo che il limite sinistro di una funzione si indica con l'apice meno e significa che si calcola il limite per valori inferiori e quindi per valori che stanno a sinistra del valore di riferimento.
Il limite destro invece si indica con un segno + ad apice e significa che si calcola il limite per valori superori e quindi per valori che stanno a destra del valore di riferimento.
Con notazione matematica si può scrivere che:
se e solo se
Una funzione f(x) è continua in x = a se:
- f(a) è definito;
esiste;
Limiti e continuità
C'è differenza tra un limite che esiste in un punto del dominio di una funzione e la continuità della funzione nel punto? Sì.La continuità impone una condizione più forte. Infatti, perché un limite esista è irrilevante che il valore della funzione esista in x = a, o anche che appartenga al dominio della funzione.
Per la continuità, noi dobbiamo poter valutare la funzione in a, e il valore f(a) deve coincidere con il limite di f(x) in a.
Questo limite esiste ed è 1 se x è misurato in radianti, ma 0 non appartiene al dominio di
Esistono vari modi di calcolare i limiti.
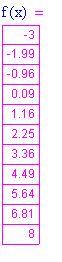
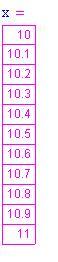
- Definiamo una lista di valori che si avvicini ad a e si calcoli il valore della funzione in ciascuno di questi punti. Se i valori della funzione si avvicinano quanto si vuole ad un unico numero, quel numero è il limite.
I numeri nella colonna di destra tendono a 8 quando la variabile indipendente tende a 11. - Se le funzioni sono polinomi, radici, seni, coseni, esponenziali, o una combinazione algebrica di queste funzione (somma, differenza, prodotto, o quoziente), proviamo a sostituire il numero a cui tende la variabile indipendente per ottenere il limite.
Se l'espressione del limite non si pone nella forma[math]\frac{0}{0}[/math]o[math]\frac{\infty}{\infty}[/math], allora abbiamo raggiunto il risultato.
Poniamo[math]\frac{p}{2}[/math]al posto di q.
Poniamo 2 al posto di t. - Se quando sostituiamo 1 alla variabile indipendente otteniamo una forma del tipo [math]\frac{0}{0}[/math]o[math]\frac{\infty}{\infty}[/math], proviamo a scomporre in fattori l'espressione dentro il segno di limite per eliminare il denominatore.
Se sostituiamo 1 a t otteniamo[math]\frac{0}{0}[/math]. Prima di sostituire, possiamo fattorizzare il numeratore:
Ora sostituiamo 1 a t:
dà
Limite per x che tende a [math]\pm \infty[/math]
Che succede se la variabile tende a Nessun problema se non troviamo forme indeterminate
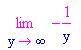
dà
perchè dà
Se quando sostituiamo otteniamo
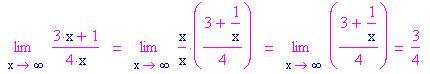
?
otteniamo un insieme di numeri compresi tra 1 e -1.
Questo è un caso in cui ottieni una risposta equivoca.
Questo limite non esiste! Ciò succede perché la funzione coseno è periodica e così assume tutti i valori compresi tra -1 e 1.
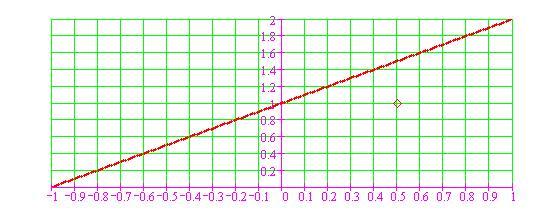
Ecco l'esempio di una funzione che ammette limite per x = 0,5, ma non è continua in x = 0,5.
La discontinuità nel punto 0,5 è evidenziata nel grafico.
Il limite esiste in x = 0,5, perchè più ci avviciniamo a 0,5, più la funzione si avvicina a 1,5.
dà
dà
Dunque, func(x) non è continua per x = 0,5.
Per essere continua, func(0,5) deve esistere ed essere uguale a 1,5:
Per ulteriori approfondimenti suile forme indeterminate vedi anche qua
Esercizio
Il prezzo del biglietto di un cinema èQual è
Il prezzo è una funzione continua?
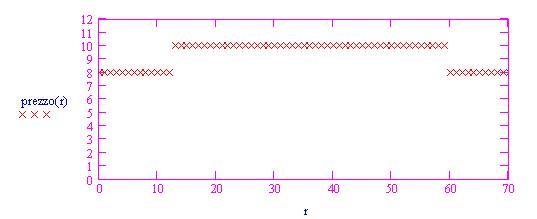
Grafico di prezzo(w):
Calcoliamo i limiti destro e sinistro per w tende a 12.
perché prezzo(w) = 8 per ogni valore di w=12.
perché per età inferiori di 12 e superiori di 60, si ha che: prezzo(w) = 10.
Poiché questi limiti sono diversi, prezzo(w) non ha il limite per w che tendente a 12. Ciò risponde esaurientemente alla domanda sulla continuità: prezzo(w) non è continua per w = 12; sebbene prezzo(12) sia definita, il limite per w tendente a 12 non esiste.