Classificazione dei fasci di parabole

I fasci di parabole si dividono in tipi diversi a seconda dei coefficienti delle parabole generatrici. Quando di qui in avanti parleremo di ( Delta ), ci riferiremo a quello dell'equazione

[ \begin{equation} (a_1-a_2)x^2+(b_1-b_2)x+(c_1-c_2)=0 label{eq1} end{equation} ]

ottenuta per ?=−1 dall'equazione del fascio

[ \begin{equation} Phi: (k+1)y=(a_1+ka_2)x^2+(b_1+kb_2)x+(c_1+kc_2) label{eq2} end{equation} ]

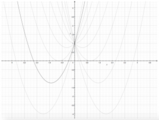
Nelle immagini, le parabole in nero sono le generatrici del fascio, mentre quelle in grigio tratteggiato sono altre parabole appartenenti al fascio ( Phi ).

Tipo 1: ( a_
e a_2, Delta gt 0 )

Se

ed sono distinti, l'equazione ((\ref{eq1})) non si riduce ad una di primo grado; il fatto poi che sia (Delta gt 0 ) assicura l'esistenza di due punti base, che nell'immagine abbiamo indicato con ? e ?. Siccome l'equazione ((\ref{eq1})) si ottiene per ?=−1, essa è una particolare parabola

del fascio, che però degenera in due rette: esse sono le rette ( x=x_A ) e ( x=x_B ), in rosso nel grafico. Per ( k = -a_1/a_2 ), l'equazione del fascio ((\ref{eq2})) si riduce a quella di una retta, ovvero a una parabola degenere; poiché deve passare per i punti base, si tratta della retta blu ??. Si noti che non può mai capitare il caso che ( -a_1/a_2=-1 ), perchè per ipotesi è (a_1
e a_2 ).

Tipo 2: ( a_1
e a_2, Delta = 0 ).

Questo caso è molto simile al precedente, ma differisce da esso per il fatto che, essendo ( Delta = 0 ), l'equazione ((\ref{eq1})) ha un solo risultato: ciò implica l'esistenza di un unico punto base ? e che la parabola che prima degenerava in due rette verticali si riduce alla retta ( x=x_T ).

Poiché, come prima, non può risultare ( -a_1/a_2=-1 ), la retta blu e quella rossa non sono coincidenti; visto che la retta rossa è verticale, quella blu dunque non può esserlo. Essendo la retta blu una parabola del fascio, essa interseca tutte le altre nel solo punto ?; non essendo poi verticale, essa non è secante in un sol punto alle parabole, ma tangente a tutte esse. Ciò dimostra anche che tutte le parabole sono tra loro tangenti in ?.

Tipo 3: ( a_1
e a_2 , Delta lt 0 ).

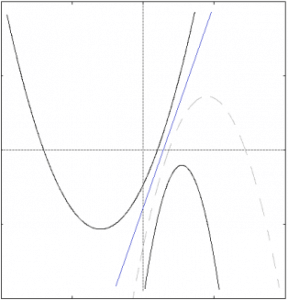
L'equazione ((\ref{eq1})) in questo caso è di secondo grado, ma non ha soluzioni reali: ciò implica l'inesistenza di punti base, e dunque tutte le parabole sono tra loro disgiunte. La parabola degenere che si ottiene per ( k = -a_1/a_2 ), ovvero la retta blu del grafico, è anch'essa tale da non intersecare alcuna delle parabole del fascio. Si noti altresì che essa è l'unica retta del piano con tale proprietà.

Tipo 4: ( a_1 = a_2, b_1
e b_2 )

Adesso l'equazione ((\ref{eq1})) non è più di primo secondo grado, ma di primo: dunque essa avrà sempre una e una sola soluzione, ovvero l'ascissa dell'unico punto base ?. Come anche nel caso 2, la retta rossa ( x = x_A ) è una parabola degenere del fascio, ottenuta come al solito ponendo ?=−1. Da questo tipo di fascio in avanti non esistono più le parabole degeneri che indicavamo in blu, poiché l'uguaglianza

implica che ( -a_1/a_2 = -1 ), e perciò esse coincidono con le rette rosse.

È poi facile vedere che, qualora esistessero due parametri â„Ž e ? tali che le parabole ad essi corrispondenti fossero tangenti in ?, allora una loro combinazione lineare particolare darebbe come risultato la loro comune retta tangente, che sarebbe ancora una parabola del fascio. Siccome tale retta non esiste, possiamo concludere che le parabole di questo tipo di fascio sono tutte secanti in ?.

Tipo 5: ( a_1 = a_2, b_1 = b_2 )

Analizziamo in ultimo il caso in cui i coefficienti delle

e delle ? delle parabole generatrici sono tra loro uguali; si ricordi che in questo caso si ha certamente ( c_1
e c_2 ), altrimenti ( Pi_1 ) e ( Pi_2 ) sarebbero la stessa parabola, contro l'ipotesi fatta in definizione 1. Se sostituiamo tali informazioni nell'equazione ((\ref{eq2})) del fascio, abbiamo

[ Phi: y=frac{a_1+ka_1}{k+1}x^2+frac{b_1+kb_1}{k+1}x+frac{c_1+kc_2}{k+1} Rightarrow y=a_1x^2+b_1x+frac{c_1+kc_2}{k+1} ]

Dunque tutte le parabole del fascio sono tra loro congruenti, e i loro grafici sono tutti traslati verticalmente l'uno rispetto all'altro. Ciò implica, in primo luogo, che essi non si intersecano, e quindi non esistono punti base; inoltre tutte le parabole condividono lo stesso asse di simmetria, corrispondente alla retta viola ? indicata in figura.

Vale la pena evidenziare che in questo caso l'equazione ((\ref{eq1})) diventa impossibile, e quindi non esistono parabole degeneri; in particolare la retta ? non è una parabola degenere del fascio, ma è sia il luogo dei vertici che quello dei fuochi di tutte le parabole.

Esercizio proposto

Sia dato il fascio di parabole di equazione ((m+1)x^2-4(m+1)x-(m+1)y+4+5m=0 ):

1. Studiare il fascio;
2. Determina la parabola cui appartiene il punto A(3; -3);
3. Determina la parabola che intercetta sull'asse x un segmento lungo 6;
4. Determina la parabola che tange la retta (2x-y-3=0);
5. Determina la parabola che forma nel 1° quadrante un triangolo mistilineo di area (frac{8}{3}).

Confronta la tua soluzione con quella (parziale) data nel forum di Matematicamente.