Equazione della parabola

(320 punti)

9' di lettura

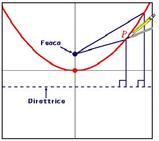
Definizione di parabola

Definizione 1: Definizione di parabola

Siano fissati una retta ? e un punto ?. Si chiama parabola di retta direttrice ? e fuoco ? il luogo geometrico dei punti del piano equidistanti da ? e da ?.

Definizione 2: Vertice di una parabola

Data una parabola ( Pi ) di direttrice ? e fuoco ?, si chiama vertice della parabola il punto ? ad essa appartenente che si trova a minima distanza dalla retta direttrice e dal fuoco.

Definizione 3: Asse di simmetria di una parabola

Data una parabola ( Pi ) di direttrice ? e fuoco ?, si chiama asse di simmetria della parabola la retta ? perpendicolare alla direttrice e passante per il fuoco (e dunque inevitabilmente anche per il vertice).

Osservazione 1: Se vale la relazione ( F in d ), cioè se il Fuoco appartiene alla direttrice, allora il luogo geometrico è banalmente la retta perpendicolare a ? passante per ?.

Si suole dire che questa retta è una parabola degenere. In questo caso naturalmente il vertice, dovendosi trovare a distanza minima dal fuoco e potendovi coincidere, è ?=?; inoltre l'asse di simmetria della parabola coincide con la stessa parabola degenere.

Osservazione 2: L'asse di simmetria è così chiamato, com'è semplice immaginare, perché il grafico della parabola risulta simmetrico rispetto ad esso. Ciò significa che se un punto ? appartiene alla parabola ( Pi ), allora anche il suo riflesso ?…² rispetto alla retta ? appartiene a ( Pi ). D'altra parte, essendo

[math] d _|_ a [/math]

, la distanza tra ? e la retta direttrice è identica a quella tra ?…² e la retta direttrice; inoltre, visto che ( F in a ), necessariamente ??=?…²?. Allora

[ \text{dist}(P', d) = \text{dist}(P, d) = PF = P'F ]

col che le distanze di ?…² dalla retta direttrice e dal fuoco sono uguali, e ( P' in Pi ).

Equazione della parabola con asse di simmetria parallelo all'asse ?

Metodo per ricavare l'equazione: Concentriamoci per il momento su di una parabola non degenere il cui asse di simmetria sia parallelo all'asse delle ordinate; ciò, in virtù della definizione 3, implica che la direttrice è una retta parallela all'asse delle ascisse, cioè che essa è ( d: y = y_d) , con

[math]y_d[/math]

un fissato numero reale. Il fuoco sia invece il punto ( F(x_F, y_F) ).

Se adesso un generico punto ?(?,?) appartiene alla parabola, dovrà risultare ????(?,?)=??; esplicitando questa affermazione in formule, avremo

[ |y-y_d|=\sqrt{(x-x_F)^2+(y-y_F)^2} ]

Calcolando i quadrati di entrambi i membri di questa equazione e isolando l'incognita ? al primo membro otterremo quindi

[ (y-y_d)^2=(x-x_F)^2+(y-y_F)^2 ]

[ y^2+y^2_d-2yy_d=x^2+x^2_F-2xx_F+y^2+y^2_F-2yy_F ]

[ 2yy_F-2yy_d=x^2+x^2_F-2xx_F-y^2_d+y^2_F ]

[ 2y(y_F-y_d)=x^2-2xx_F+(x^2_F+y^2_F-y^2_d) ]

Se la parabola non è degenere, per l'osservazione 1 ? non appartene a ?; ne consegue che ( y_F
e y_d ), e quindi si possono dividere ambo i membri dell'ultima equazione per il valore non nullo ( 2(y_F-y_d) ), ottenendo

[ \begin{equation} y=frac{1}{2(y_F-y_d)}x^2-frac{x_F}{y_F-y_d}x+frac{(x^2_F+y^2_F-y^2_d)}{2(y_F-y_d)} label{eq1} end{equation} ]

La ((\ref{eq1})) è la generica equazione di una parabola non degenere con asse parallelo all'asse ?. Più semplicemente, essa si scriverà come ( y=ax^2+bx+c ) una volta fatte le posizioni

[ a=frac{1}{2(y_F-y_d)} ,,,, , ,,,, b=-frac{x_F}{y_F-y_d} ,,,, , ,,,, c=frac{(x^2_F+y^2_F-y^2_d)}{2(y_F-y_d)} ]

Osservazione 3: Notiamo subito che, per il modo in cui è definito, ( a
e 0 ). D'altro canto, se risultasse ?=0 l'equazione ((\ref{eq1})) diventerebbe di primo grado, e finirebbe dunque come sappiamo col rappresentare una retta.

Osservazione 4: Il fatto che l'asse di simmetria sia parallelo all'asse ? e che esso passi per il fuoco ci dice che l'equazione dell'asse è ( x = x_F ). Scritta in funzione dei parametri ?,?,? che definiscono la parabola, essa diventa ( x=-frac{b}{2a} ); è infatti facile vedere che

[ -frac{b}{2a}=-Big(-frac{x_F}{y_F-y_d}Big):Big(frac{2}{2((y_F-y_d)}Big)=frac{x_F}{y_F-y_d}(y_F-y_d)=x_F ]

Osservazione 5: È possibile scrivere l'equazione della retta direttrice in funzione di ?,?,?. Essa risulta essere ( y =-frac{1+b^2+4ac}{4a} ), o come anche si suole scrivere ( y = -frac{1+Delta}{4a} ), avendo posto come al solito ( Delta = b^2-4ac ). Infatti

[ -frac{1+Delta}{4a} = -frac{1+b^2-4ac}{4a}=-frac{1}{4a}-aBig(-frac{b}{2a}Big)^2+c = ]

[ = frac{y_d-y_F}{2}-frac{x^2_F}{2(y_F-y_d)}+frac{(x^2_F+y^2_F-y^2_d)}{2(y_F-y_d)}=frac{y_d-y_F}{2}+frac{y^2_F-y^2_d}{2(y_F-y_d)}=frac{y_F+y_d}{2}+frac{y_d-y_F}{2}=y_d ]

Osservazione 6: L'ordinata del fuoco può essere trovata come ( y_F=frac{1-Delta}{4a} ), poichè grazie all'osservazione 5 possiamo scrivere direttamente, senza tanti calcoli,

[ frac{1-Delta}{4a}=frac{2}{4a}-frac{1+Delta}{4a}=frac{1}{2a}+y_d=(y_F-y_d)+y_d=y_F ]

Osservazione 7: L'ordinata del vertice si trova con la seguente considerazione: poiché il fuoco e il vertice appartengono entrambi all'asse di simmetria, il quale è perpendicolare alla direttrice, che è a sua volta parallela all'asse ?, le distanze del vertice dal fuoco e dalla direttrice si trovano semplicemente sottraendo tra loro le ordinate. Siccome però il vertice appartiene alla parabola, le due distanze devono essere uguali, e perciò

[ y_V-y_d = y_F-y_V Rightarrow y_V=frac{(y_F-y_d)}{2}=frac{1}{2}Big(frac{1-Delta}{4a}-frac{1+Delta}{4a}Big)=-frac{Delta}{4a} ]

Osservazione 8: Riassumiamo qui tutto quanto trovato nel corso di questo paragrafo, e confrontiamolo con il grafico di una parabola con asse parallelo all'asse ?:

Grafico della parabola

[ Pi: y=ax^2+bx+c,,,,, ,,,,,, a
e 0 ]

[ FBig(-frac{b}{2a}, frac{1-Delta}{4a}Big) ,,, , ,,, VBig(-frac{b}{2a}, -frac{Delta}{4a}Big) ,,, , ,,, \text{direttrice: } y=-frac{1+Delta}{4a} ,,, , ,,, \text{asse: } x=-frac{b}{2a} ]

Equazione della parabola con asse di simmetria parallelo all'asse ?

Osservazione 9: Vogliamo adesso interessarci del caso di una parabola avente l'asse di simmetria parallelo all'asse delle ascisse. Come il lettore non stenterà a credere, tanto il metodo che consente di ricavare l'equazione della parabola a partire dalla definizione, tanto i risultati ottenuti riguardo gli elementi della parabola sono del tutto simmetrici a quelli del caso in cui l'asse di simmetria è parallelo all'asse delle ordinate. Ci limiteremo quindi ad elencarli:

Parabola con asse di simmetria parallelo all'asse dell'ascisse

[ Pi: x=ay^2+by+c,,,,, ,,,,,, a
e 0 ]

[ FBig(frac{1-Delta}{4a},-frac{b}{2a} Big) ,,, , ,,, VBig(-frac{Delta}{4a},-frac{b}{2a} Big) ,,, , ,,, \text{direttrice: } x=-frac{1+Delta}{4a} ,,, , ,,, \text{asse: } y=-frac{b}{2a} ]

Osservazione 10: L'unica sostanziale differenza tra i due casi osservati è che, mentre nel primo caso l'equazione ottenuta era quella di una funzione di ?, nel secondo caso ciò non è vero: una parabola con asse parallelo all'asse delle ? non è una funzione. Infatti, com'è facile vedere dal grafico, per ogni valore di ( x gt x_V ) ci sono due differenti valori di ? che gli corrispondono, uno al di sopra e uno al di sotto dell'asse di simmetria. Quando, per applicazioni più avanzate, si adopera una parabola di questo tipo, ci si riferisce solitamente alla funzione costituita dal suo solo ramo superiore.