_stan
di _stan
(320 punti)
7' di lettura

Definizioni

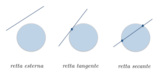
Definizione 1: Rette incidenti

Due rette r ed s si dicono incidenti quando si intersecano in uno e in un solo punto.

Definizione 2: Rette parallele

Due rette r ed s si dicono parallele quando la loro intersezione è vuota. Questa eventualità si indica con il simbolo (

[math] r ⊥ s [/math]
).

Definizione 3: Rette coincidenti

Due rette r ed s si dicono coincidenti quando si intersecano in più di un punto.

Definizione 4: Rette ortogonali o perpendicolari

Si considerino due rette incidenti a ed c.

Esse si dicono ortogonali quando i quattro angoli da esse formati nell’unico punto d’intersezione sono tutti retti. Questa eventualità si indica con il simbolo

[math] a ⊥ c [/math]
.Geometria analitica: rette ortogonali

Osservazione 1:
Le definizioni 1 – 3 tengono in considerazione tutti i casi possibili: infatti non solo due rette, ma più in generale due qualsiasi curve o non si intersecano, o si intersecano in un solo punto, o si intersecano in più di un punto. Vale però la pena di notare che, poiché per due punti passa una e una sola retta, allorché due rette hanno due o più punti in comune esse si sovrappongono completamente. I punti d’intersezione sono allora infiniti, e le due rette coincidono.

Osservazione 2:
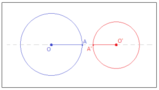
Nell’immagine precedente, le rette a ed b sono parallele, poiché come si vede non hanno punti in comune; invece la retta c e ortogonale alla retta a, e di conseguenza anche alla sua retta parallela b, come segue da un noto teorema di geometria piana. La retta d, infine, è incidente sia con a che con b; si noti che, benché il punto d’intersezione non sia mostrato, c è evidentemente incidente anche con d.

Condizioni di parallelismo e ortogonalità

Numero di intersezioni:
Siano date due rette r ed s le cui equazioni in forma esplicita sono

[math] r: y = m_rx + q_r , s: y = m_sx + q_s [/math]

con

[math] m_r, m_s, q_r, q_s [/math]
numeri reali fissati. Vogliamo trovare delle relazioni tra questi quattro valori che siano in grado di dirci se r ed s sono coincidenti, parallele o incidenti, e in questo caso vogliamo distinguere anche l’eventualità che r ed s siano ortogonali. Analizziamo a questo proposito il sistema

[math] \begin{cases} y = m_rx + q_r \\ y = m_sx + q_s \end{cases} \Rightarrow [/math]

[math] \Rightarrow \begin{equation} m_rx + q_r = m_sx + q_s \Rightarrow (m_r - m_s)x = q_s - q_r \label{eq1} \end{equation} [/math]

La x contenuta nell’ultima equazione è l’ascissa dell’eventuale punto d’intersezione. Dal momento che l'equazione è di primo grado, o è impossibile, o è indeterminata, o è dotata di una e una sola soluzione. Il caso d’impossibilità si ottiene allorché

[math] m_r - m_s = 0 , q_s - q_r \neq 0 [/math]

cioè se e solo se

[math] m_r = m_s [/math]
e
[math] q_r \neq q_s [/math]
. In questo caso le rette, che avendo intercette diverse sono necessariamente distinte, non hanno intersezioni e sono perciò parallele. Il caso d’indeterminazione si ha invece allorché

[math] m_r - m_s = 0 , q_s - q_r = 0 [/math]

In questo caso le soluzioni sono tutte le x reali, e infatti senza sorpresa ci accorgiamo che richiedere

[math] m_r = m_s [/math]
e
[math] q_r = q_s [/math]
equivale a considerare due rette coincidenti. Se invece infine abbiamo
[math] m_r \neq m_s [/math]
, allora l'equazione si può riscrivere nella forma

[math] x = - \frac{q_r - q_s}{m_r - m_s} [/math]

la quale evidenzia l’esistenza di una e una sola soluzione. Le rette r ed s saranno allora incidenti. Ricapitolando:

[math] m_r = m_s \text{ e } q_r \ne q_s \Rightarrow r \text{ ed } s \text{ sono parallele} [/math]
[math] m_r = m_s \text{ e } q_r = q_s \Rightarrow r \text{ ed } s \text{ sono coincidenti}[/math]
[math] m_r \ne m_s \Rightarrow r \text{ ed } s \text{ sono incidenti} [/math]

Condizione di ortogonalità:
Se due rette a e b sono ortogonali, allora è anche vero che tutte le rette parallele ad a sono ortogonali a tutte le rette parellele a b; poiché le relazioni di parallelismo e orotogonalità sono simmetriche, per mostrare che

[math] a ⊥ b [/math]
ci basta fare vedere che esistono
[math] r || a, s || b [/math]
tali che
[math] r ⊥ s [/math]
.

Siano dunque ? e ? due rette fissate, e siano ? ed ? le uniche rette passanti per l’origine del sistema di coordinate rispettivamente parallele ad ? e a ?, tra loro ortogonali. Siccome ? ed ? passano per l’origine, esse avranno forma

[math] y = mx [/math]
; poiché inoltre vale il parallelismo con ? e ?, in virtù della conclusione del paragrafo precedente abbiamo
[math] m_r = m_a [/math]
e
[math] m_s = m_b [/math]
. Le equazioni di ? ed ? sono perciò

[math] r: y = m_a x , s: y = m_b x [/math]
Geometria analitica: rette perpendicolari

Siano ora ? e ? i punti di ascissa 1 di ? ed ?, cioè risulti come nell’immagine

[math] A(1, m_a) [/math]
e
[math] B(1, m_b) [/math]
. La distanza tra ? e ? è
[math] |m_a - m_b | [/math]
, dal momento che essi sono verticalmente allineati; inoltre dal per il teorema di Pitagora abbiamo
[math] OA = \sqrt{1+m^2_a} [/math]
e
[math] OB = \sqrt{1+m^2_b} [/math]
. Applicando ancora il teorema di Pitagora,

[math] |m_a - m_b | = AB = \sqrt{OA^2 + OB^2} = \sqrt{1+m^2_a+1+m^2_b} [/math]

ed elevando al quadrato il primo e l’ultimo membro

[math] m^2_a + m^2_b - 2m_am_b = 2 + m^2_a + m^2_b \Rightarrow m_a m_b = -1 [/math]

L’ultima ottenuta è la desiderata relazione di ortogonalità tra le rette ? e ?.

Altro materiale di supporto

Videolezione sulle rette perpendicolari e parallele

Videolezione geometria analitica: rette perpendicolari e parallele

Vuoi approfondire Geometria - Formule e problemi di geometria con un insegnante esperto?
Trovalo su Ripetizioni.it