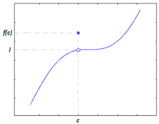
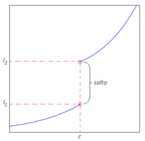
Definizione di discontinuità di seconda specie
Definizione 1: Discontinuità di seconda specie.
Sia
[math]f(x)[/math]
una funzione di dominio
[math]D \in \mathbb{R}[/math]
discontinua in
[math]c[/math]
. Tale punto
[math]c[/math]
si dice essere una
discontinuità di seconda specie per
[math]f(x)[/math]
qualora risulti che almeno uno dei due limiti destro o sinistro della funzione non esiste, oppure
[math] \displaystyle \lim_{x\rightarrow c^{-}} f(x) = \infty \mbox{ o } \lim_{x \rightarrow c^{+}} f(x) = \infty [/math]
Definizione 2: Asintoto verticale destro e sinistro.
Se il limite destro (rispettivamente, sinistro) di una funzione
[math]f(x)[/math]
in una sua discontinuità di seconda specie
[math]c[/math]
è infinito, allora si dice che la retta di equazione
[math]x = c[/math]
è per
[math]f(x)[/math]
un asintoto verticale destro (rispettivamente sinistro).
Definizione 3: Asintoto verticale.
Se la retta di equazione
[math]x = c[/math]
sia asintoto verticale destro che asintoto verticale sinistro per la funzione
[math]f(x)[/math]
, allora essa detta semplicemente essere un asintoto verticale per
[math]f(x)[/math]
.

Osservazione 1: Perché
[math]c[/math]
sia una discontinuità di seconda specie per
[math]c[/math]
, tale punto non deve necessariamente appartenere al dominio della funzione, ma basta che ne sia punto di accumulazione.
Anche nel caso in cui risulti
[math]c \in D[/math]
, la definizione 1 è indipendente dal valore di
[math]f(c)[/math]
.
Osservazione 2: Se
[math]c[/math]
è una discontinuità di seconda specie per
[math]c[/math]
, allora uno dei limiti destro o sinistro della funzione per
[math]x \rightarrow c[/math]
può anche esistere ed essere finito. Infatti nella definizione 1 si dice che a non esistere o ad essere infinito deve'ssere almeno uno dei due limiti suddetti.
Esempi di funzioni con discontinuità di seconda specie
Esempio 1: I limiti destro e sinistro non esistono.
Sia
[math]f(x[/math]
la funzione data dallequazione
[math]y = \sin\Big(\frac{1}{x}\Big)[/math]
, informalmente nominata seno del topologo, il cui grafico è approssimato dall'immagine seguente:

Verifichiamo che essa possiede una discontinuità di seconda specie per
[math]x = 0[/math]
. A questo proposito calcoliamo i limiti destro e sinistro:
[math] \displaystyle \lim_{x \rightarrow 0^{-}} \sin\Big(\frac{1}{x}\Big) = \sin(-\infty) \rightarrow \mbox{ non esiste} [/math]
[math] \displaystyle \lim_{x \rightarrow 0^{+}} \sin\Big(\frac{1}{x}\Big) = \sin(+\infty) \rightarrow \mbox{ non esiste} [/math]
I due passaggi immediatamente dopo l'uguale non sono leciti, ma servono a far intendere il ragionamento che porta alla determinazione del risultato: allorché
[math]x \rightarrow 0^{\pm}[/math]
il valore di
[math]1/x[/math]
si avvicina a
[math]\pm\infty[/math]
, ma la funzione seno periodica e continua ad oscillare tra -1 e 1 per
[math]x[/math]
comunque grande. Ciò significa che in ogni intervallo centrato nell'origine la
[math]f(x)[/math]
assume tutti i valori compresi nell'intervallo [-1,1], cosicché i limiti ricercati non esistono. Ci dimostra che 0, che naturalmente non appartiene al dominio della funzione, è per essa una discontinuità di seconda specie.
La frequenza delle oscillazioni che la funzione possiede nelle vicinanze dell'origine, tanto maggiore quanto più ci si avvicina alla discontinuità, rende impossibile la raffigurazione di un grafico preciso: è per questo che nell'immagine esso è stato solo approssimato.
Esempio 2: I limiti destro e sinistro sono infiniti.
Si consideri adesso la funzione
[math]y = \frac{\cos x}{x^2}[/math]
, rappresentata nel grafico sottostante:

Il suo dominio è
[math]D = \mathbb{R} - {0}[/math]
, cioé la funzione è definita ovunque, ad esclusione del punto
[math]x = 0[/math]
. Vogliamo verificare che in tale punto la funzione presenta invece una discontinuità di seconda specie, e a questo scopo calcoliamo i limiti destro e sinistro come richiesto dalla definizione 1:
[math] \displaystyle \lim_{x \rightarrow 0^{-}} \frac{\cos x}{x^2} = +\infty = \lim_{x \rightarrow 0^{+}} \frac{\cos x}{x^2} [/math]
Il risultato chiaramente infinito, poiché il coseno è una funzione continua che vale 1 in 0, mentre invece
[math]x^2[/math]
tende a 0. In entrambi i casi otteniamo poi
l'infinito positivo, visto che la funzione in esame è pari, ovvero dotata di grafico simmetrico rispetto all'asse delle
[math]y[/math]
. Dal momento che entrambi i limiti considerati sono infiniti,
[math]x = 0[/math]
è effettivamente una discontinuità di seconda specie per la funzione considerata, come previsto. La definizione 3 assicura infine che la retta di equazione
[math]x = 0[/math]
è un asintoto verticale per la nostra funzione.
In questo caso il fatto che il grafico della funzione oscilli non crea problemi come nell'esempio precedente, poiché tali oscillazioni non si fanno sempre più frequenti man mano che
[math]x[/math]
tende a 0.
Esempio 3: Uno solo dei due limiti è infinito e
[math]c[/math]
non appartiene a
[math]D[/math]
.
Il prossimo caso cui vogliamo interessarci è quello della funzione
[math]y = e^{\frac{1}{x}}[/math]
, rappresentata nel
piano cartesiano dal grafico seguente:

È facile osservare che il grafico della funzione si spezza in corrispondenza del punto
[math]x = 0[/math]
, il che suggerisce che in tale punto vi sia una discontinuità. Verifichiamo, tramite applicazione dei limiti nella definizione 1, che si tratta effettivamente di una discontinuità di seconda specie.
[math] \displaystyle \lim_{x \rightarrow 0^{+}} e^{\frac{1}{x}} = \lim_{z \rightarrow +\infty} e^z = +\infty [/math]
Nella seconda uguaglianza abbiamo adoperato il cambio di variabile
[math]z = \frac{1}{x}[/math]
. Come si vede il risultato ottenuto è infinito, e questo già è sufficiente a dire che
[math]x = 0[/math]
è una discontinuità di seconda specie, come da osservazione 2; inoltre la definizione 2 assicura che la retta di equazione
[math]x = 0[/math]
è un asintoto verticale destro per la funzione esaminata. Per completezza calcoliamo anche il limite sinistro:
[math] \displaystyle \lim_{x \rightarrow 0^{-}} e^{\frac{1}{x}} = \lim_{z \rightarrow -\infty} e^z = 0^{+} [/math]
Si può osservare che il risultato in questo caso è un numero finito. Ad ogni modo, poiché
[math]x = 0[/math]
non appartiene al dominio della funzione, il punto
[math]O(0, 0)[/math]
non appartiene al suo grafico, ed è stato per questo indicato con un cerchio vuoto. A ulteriore dimostrazione di ciò, si consideri che
[math]e^{1/x} \gt 0, \forall x \in \mathbb{R}[/math]
: ciò significa che la funzione non può annullarsi in alcun punto.
Esempio 4: Uno solo dei due limiti non esiste e
[math]c[/math]
appartiene a
[math]D[/math]
.
L'ultimo caso che esamineremo è quello della funzione
[math]y = {x}\sin\Big(\frac{1}{x}\Big)[/math]
, rappresentata dal grafico in blu più sotto. La funzione che indichiamo con
[math]{x}[/math]
è nominata parte frazionaria di
[math]x[/math]
, o mantissa di
[math]x[/math]
: dato un numero reale
[math]x[/math]
, essa gli fa corrispondere la sua parte decimale, ovvero
[math]x - \mbox{floor}(x)[/math]
; ad esempio,
[math]{2.75}=0.75 , {\pi}=0.14159 \ldots, {2}=0[/math]
.

Poiché i valori assunti dal seno sono tutti e soli quelli compresi tra -1 e 1, il grafico della funzione in esame sarà tutto compreso tra il grafico della mantissa di
[math]x[/math]
e il suo opposto, entrambi rappresentati nell'immagine soprastante con linee grigie tratteggiate. Quindi
[math] -{x} \le {x} \sin\Big(\frac{1}{x}\Big) \le {x} [/math]
e per il teorema del confronto avremo perciò
[math] \displaystyle 0 = \lim_{x \rightarrow 0^{+}} -{x} \le \lim_{x \rightarrow 0^{+}} {x} \sin\Big(\frac{1}{x}\Big) \le \lim_{x \rightarrow 0^{+}} {x} = 0 [/math]
il che assicura che il limite destro per
[math]x \rightarrow 0[/math]
della funzione considerata esiste ed nullo. Consideriamo adesso lo stesso limite, ma a sinistra:
[math] \displaystyle 0 = \lim_{x \rightarrow 0^{-}} {x} \sin\Big(\frac{1}{x}\Big) = \lim_{x \rightarrow 0^{-}} 1 \cdot \sin\Big(\frac{1}{x}\Big) = \lim_{x \rightarrow 0^{-}} \sin\Big(\frac{1}{x}\Big) [/math]
Come risulta dalla discussione dell'esempio 1, tale limite è oscillante e perciò non esiste.
Ciò ci dice che il punto
[math]x = 0[/math]
è una discontinuità di seconda specie per la funzione
[math]f(x)[/math]
esaminata. pure interessante notare che in questo caso
[math]{0} \in D[/math]
, visto che risulta
[math]f(0) = 0[/math]
; dunque anche se la funzione nel punto
[math]c[/math]
considerato è definita e uno dei limiti, in questo caso quello destro, tende al valore
[math]f(c)[/math]
della funzione, essa può comunque essere discontinua.