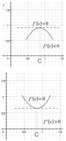
Concavità di una curva in un punto
Consideriamo una curva di equazione
[math] y = f(x) [/math]
derivabile nei punti interni di un intervallo
[math] I [/math]
, e consideriamo un punto
[math] c [/math]
interno a tale intervallo.
Si dice che la curva
[math] f(x) [/math]
ha nel punto
[math] P [/math]
di coordinate
[math] (c ; f(c)) [/math]
concavità rivolta verso il semiasse positivo delle
[math] y [/math]
se esiste un intorno del punto
[math] c [/math]
per tutti i punti del quale (escluso il punto
[math] x = c [/math]
) le ordinate dei punti sulla curva sono maggiori delle ordinate dei corrispondenti punti sulla tangente in
[math] P [/math]
.
In riferimento alla figura precedente, considerando i punti
[math] P [/math]
e
[math] Q [/math]
sulla curva, e i punti
[math] P [/math]
e
[math] T [/math]
corrispondenti della retta tangente in
[math] P [/math]
alla curva, e le loro proiezioni
[math] C [/math]
e
[math] H [/math]
sull'asse
[math] x [/math]
, abbiamo che ( HQ gt HT ).
In questo caso, possiamo anche dire che la curva ha concavità rivolta verso l'alto.
In maniera analoga, possiamo definire la concavità verso il basso di una funzione:
Si dice che la curva
[math] f(x) [/math]
ha nel punto
[math] P [/math]
di coordinate
[math] (c ; f(c)) [/math]
concavità rivolta verso il semiasse negativo delle
[math] y [/math]
se esiste un intorno del punto
[math] c [/math]
per tutti i punti del quale (escluso il punto
[math] x = c [/math]
) le ordinate dei punti sulla curva sono minori delle ordinate dei corrispondenti punti sulla tangente in
[math] P [/math]
.
In questo caso, invece, considerando i punti
[math] P , Q, T, H [/math]
e le loro proiezioni
[math] C [/math]
e
[math] H [/math]
sull'asse
[math] x [/math]
, abbiamo che ( HQ lt HT ).
Vediamo, ora, il seguente teorema che mette in relazione la derivata seconda di una funzione con la concavità del suo grafico.
Teorema: Consideriamo la funzione di equazione
[math] y = f(x) [/math]
derivabile due volte nei punti interni all'intervallo
[math] I [/math]
, e tale che la sua
derivata seconda
[math] f''(x) [/math]
sia continua in
[math] I [/math]
; sia
[math] c [/math]
un punto interno di
[math] I [/math]
.
Allora, si ha che:
- se ( f''(x) gt 0 ), allora la curva di equazione
[math] y = f(x) [/math]
volge, nel punto di ascissa [math] c [/math]
, la concavità verso l'alto;
- se ( f''(x) lt 0 ), allora la curva di equazione
[math] y = f(x) [/math]
volge, nel punto di ascissa [math] c [/math]
, la concavità verso il basso.
Concavità di una curva in un intervallo
Se la funzione in questione volge la concavità verso l'alto o verso il basso in tutti i punti interni ad un intervallo
[math] I [/math]
, possiamo dire che la curva volge la concavità verso l'alto o verso il basso in tutto
[math] I [/math]
.
Definizione: Una funzione si dice concava verso l'alto in un intervallo
[math] I [/math]
, se il suo grafico volge la concavità verso l'alto in
[math] I [/math]
; la funzione si dice, invece, concava verso il basso in
[math] I [/math]
se il suo grafico volge la concavità verso il basso in tutto
[math] I [/math]
.
Dal teorema precedente, riguardante la concavità di una funzione in un punto, si deduce il seguente teorema:
Teorema: Consideriamo la funzione di equazione
[math] y = f(x) [/math]
derivabile due volte nei punti interni all'intervallo
[math] I [/math]
, e tale che la sua derivata seconda
[math] f''(x) [/math]
sia continua in
[math] I [/math]
. Allora, si ha che:
- se f''(x) > 0, allora la funzione f(x) è, nell'intervallo I, concava verso l'alto;
- se f''(x)
Punti di flesso
Consideriamo una funzione
[math] y = f(x) [/math]
che ammette derivata seconda in un punto
[math] c [/math]
, e tale derivata calcolata in
[math] c [/math]
è nulla ( cioè,
[math] f''(c) = 0 [/math]
), e che la derivata seconda abbia segni opposti a destra e a sinistra di
[math] c [/math]
.
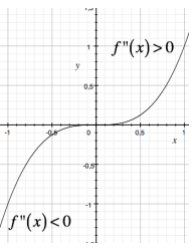La funzione in questione, quindi, nei due intorni di
[math] c [/math]
(destro e sinistro), volge concavità differenti: verso il basso da una parte, e verso l'altro dall'altra. Il punto
[math] c [/math]
che ha queste
proprietà viene definito
punto di flesso.
Possiamo, quindi, dedurre che, per determinare un punto di flesso, dobbiamo studiare il segno della derivata seconda della funzione, e verificare che la derivata seconda assuma valori di segno opposto nell'intorno sinistro e destro del punto
