Retta tangente in un punto al grafico di una funzione

La derivata di una funzione in un punto rappresenta il coefficiente angolare della retta tangente alla funzione in quel punto. Sfruttando questa relazione, è possibile determinare l'equazione della retta tangente al grafico di una funzione , conoscendo l'ascissa () del punto P in cui la retta è tangente alla curva.

Tale retta, infatti, dovrà soddisfare i seguenti requisiti:

• Sapendo che il punto P in cui la retta è tangente alla curva ha ordinata x0, e sapendo che tale punto appartiene alla curva
  [math] f(x) [/math]
  , sappiamo che la sua ordinata è
  [math] f(x_0) [/math]
  . Quindi, la retta in questione passa per il punto
  [math] P(x_0 ; f(x_0)) [/math]
  . La sua equazione sarà quindi del tipo: [ y = f(x_0) = m (x-x_0) ]dove m indica il suo coefficiente angolare.
• Sapendo, poi, che la derivata della funzione nel punto x0 rappresenta proprio il coefficiente angolare della retta cercata, abbiamo: [ m = f'(x_0) ]

Dalle relazioni precedenti, possiamo dare l'equazione della retta richiesta, ottenibile conoscendo l'ascissa del punto di tangenza, e la derivata della curva in questione in quel punto: [ y = f'(x_0) cdot (x-x_0) + f(x_0) ]

Notiamo che l'equazione precedente si riferisce ad una retta non parallela agli assi; infatti, se la retta fosse parallela all'asse

, essa avrebbe equazione .

In questo caso, la funzione non sarebbe derivabile in

, in quanto ammetterebbe derivata infinita.

Vediamo ora alcuni casi particolari, in cui nei punti in questione la funzione non è derivabile:

Punto angoloso

La funzione è continua in , ma non è derivabile in , per esempio nel caso in cui il rapporto incrementale relativo al punto non ha limite, in quanto sono diversi i limiti sinistro e destro.

In questo caso, infatti, anche le derivate destra e sinistra sono diverse, quindi la funzione non è derivabile in

, ma esisteranno due rette tangenti alla funzione nel punto , che prende il nome di punto angoloso.

Quindi: [ {f'}_{+}(x) = l_1 in mathbb{R} wedge {f'}_{-}(x) = l_2 in mathbb{R} ]

e si ha che: [ l_1
e l_2 ]

Il punto angoloso si ha anche quando una delle due derivate nel punto

(la derivata destra, o quella sinistra) è finita, e l'altra infinita, e viceversa.

[ {f'}_{+}(x) = pm infty wedge {f'}_{-}(x) = l in mathbb{R} ]

oppure:

[ {f'}_{+}(x) = l inmathbb{R} wedge {f'}_{-}(x) = pminfty ]

Cuspide

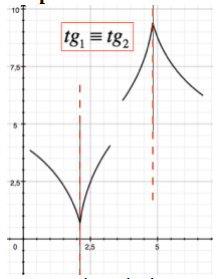
Può accadere che in un punto

, in cui la funzione non è derivabile, vi siano due rette tangenti coincidenti, che sono parallele all'asse ; si dice che il punto è una cuspide, che può essere definita come un caso particolare di punto angoloso.

In questo caso, le derivate destra e sinistra sono entrambe infinite, ma con segno opposto.

[ {{f'}_{+}(x) = +infty wedge {f'}_{-}(x) = -infty ,,,, mbox{ oppure } ,,,, {{f'}_{+}(x) = -infty wedge {f'}_{-}(x) = +infty

Flesso a tangente verticale

La funzione

non è derivabile nel punto , in quanto i valori delle derivate, destra e sinistra, sono uguali, ma entrambi infiniti.

Abbiamo quindi che: [ {f'}_{+}(x) = +infty wedge {f'}_{-}(x) = +infty ]

oppure: [ {f'}_{+}(x) = -infty wedge {f'}_{-}(x) = - infty ]