Teorema di Rolle: regole

Questo appunto di Analisi Matematica tratta l'enunciato, la dimostrazione matematica e le applicazioni del teorema di Rolle, per le funzioni reali di variabili reali.

Enunciato del teorema di Rolle

Il teorema di Rolle, insieme ai teoremi di Lagrange e di Cauchy, sono molto importanti nel campo dell'analisi matematica. In particolare, il teorema di Rolle ci permette di conoscere una funzione in un suo intervallo chiuso.
Consideriamo una funzione definita in un intervallo chiuso di estremi e , che abbia le seguenti proprietà:

• [math]f(x)[/math]
  continua in
  [math][a,b][/math]
• [math]f(x)[/math]
  derivabile in
  [math](a,b)[/math]
• [math]f(x)[/math]
  assume valori uguali agli estremi
  [math]a[/math]
  e
  [math]b[/math]
  dell'intervallo

In analisi matematica, il teorema di Rolle afferma che se la funzione possiede le proprietà sopra elencate, allora esiste almeno un punto

, detto punto critico o stazionario, interno all'intervallo, in cui la funzione ha derivata nulla, cioè tale che:

Dimostrazione del teorema

Prima di fornire la dimostrazione del teorema, enunciamo (senza dimostrarli) il teorema di Weierstrass e il teorema di Fermat poiché torneranno utili.
Teorema di Weierstrass: Dato un intervallo compatto, ovvero un intervallo chiuso e limitato, non vuoto, e data una funzione definita e continua su questo insieme. Allora, per il teorema di Weierstrass, in ammette un punto di minimo assoluto e un punto di massimo assoluto.
Teorema di Fermat: stabilisce che ogni punto di estremo locale in cui è definita una funzione è un punto stazionario della funzione, ovvero come già detto, è un punto tale per cui la derivata prima della funzione si annulli in quel punto.
Adesso, possiamo schematizzare il teorema di Rolle in questo modo:

Sia

continua in , derivabile in e se vale in

La dimostrazione del teorema di Rolle viene effettuata andando a considerare i casi in cui si verificano le ipotesi del teorema di Rolle.
Sappiamo che date le condizioni iniziali, vengono rispettate le ipotesi del teorema di Weierstrass. Pertanto, la funzione

assume nell'intervallo un valore di minimo assoluto e un valore di massimo assoluto. Chiamiamo e rispettivamente i valori minimo e massimo assunti dalla funzione nell'intervallo . In questo modo, possiamo assistere a due casi diversi.
Nel primo caso possiamo avere che il massimo assoluto e il minimo assoluto siano raggiunti dalla funzione ai suoi estremi e quindi poiché deve essere che:

Ne consegue che la funzione assume in tutto l'intervallo

lo stesso valore, il quale corrisponde a:

La funzione è, quindi, detta funzione costante e in particolare si avrà anche che:

Pertanto, in tutti i punti

dell'intervallo , la derivata della funzione sarà nulla.

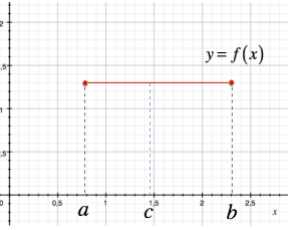
Diversamente, se il massimo e il minimo sono raggiunti all'interno dell'intervallo, allora abbiamo che:

La funzione non è costante in

. Se, ad esempio, consideriamo che il valore di massimo assoluto della funzione sia raggiunto in un punto dell'intervallo , ovvero:

Abbiamo che per le ipotesi del teorema di Fermat, il valore della derivata nel punto

è nulla.

Osservazioni

In questo caso, possiamo capire meglio il teorema di Rolle anche dal punto di vista geometrico. Sappiamo, infatti, che la derivata di una funzione in un punto rappresenta il coefficiente angolare della retta tangente alla funzione in quel punto. Se in un intervallo esiste un punto tale che si ha , allora in quel punto la tangente alla funzione è parallela all'asse .

Il teorema di Rolle è strettamente correlato al teorema di Lagrange e al teorema di Cauchy. Infatti, dimostrando uno di questi, si possono dimostrare facilmente gli altri due.
La presenza delle tre ipotesi per la dimostrazione del teorema di Rolle è fondamentale. Infatti, se la funzione

non fosse stata continua in , non avremmo potuto applicare il teorema di Weierstrass che ci assicura la presenza di un minimo e un massimo assoluto della funzione. Se la funzione non fosse stata derivabile in , non avremmo potuto applicare il teorema di Fermat sui punti stazionari il quale, appunto, garantisce la presenza dei punti stazionari.
Inoltre, nel caso in cui una delle tre ipotesi fosse violata, il teorema di Rolle non è più valido. Ovviamente ciò non implica che non possano esserci dei punti in cui la derivata si annulli, ma semplicemente questi punti tali per cui la funzione assume un valore di derivata nulla non vengono garantiti.

Esercizio svolto sul teorema di Rolle

Sia data la seguente funzione:

Determina se sussistono le ipotesi del teorema di Rolle nell'intervallo [1,4] e trova il punto che verifica il teorema.
Per constatare se sussiste la prima ipotesi del teorema, dobbiamo chiederci se la funzione sia continua nell'intervallo [1,4]. Pertanto, dobbiamo individuare il dominio della funzione. In questo caso abbiamo che il denominatore deve essere diverso da 0, ovvero:

Si ha che il denominatore è diverso da

sempre, per cui il dominio della funzione è tutto l'insieme dei numeri reali. A maggior ragione abbiamo che la funzione sia definita e continua nell'intervallo , ed è anche derivabile. Passando a verificare se viene rispetatta la terza condizione del teorema di Rolle, dobbiamo calcolare il valore della funzione agli estremi dell'intervallo considerato ovvero:

Dunque, essendo

, sono verificate tutte le ipotesi del teorema di Rolle. Esisterà allora un punto c appartenente all'intervallo considerato , tale per cui:

Ricordando la derivata del rapporto, calcoliamo adesso la derivata prima di f(x):

Per trovare il punto

che soddisfi il teorema, scriviamo:

=0

Risolvendo si ha che l'equazione si riduce a:

Quindi il numero che soddisfa il teorema di Rolle è

, il quale è l'unico interno all'intervallo .

Per ulteriori approfondimenti sul teorema di Rolle, vedi qui