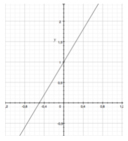
Definizione di disequazione
Le disequazioni ad un’incognita sono espressioni letterali con una disuguaglianza tra i membri dell’espressione stessa. Risolvere una disequazione vuol dire quindi individuare un intervallo di numeri reali che verificano la disuguaglianza.
Insieme delle soluzioni di una disequazione
L’insieme delle soluzioni di una disequazione contiene tutti quei numeri reali che, sostituiti all’incognita, rendono la disequazione vera. A differenza delle equazioni, le disequazioni possono presentare un insieme di soluzioni costituito anche da infiniti valori.Risolvere una disequazione significa quindi determinare l’insieme di valori che verifica la disequazione.
Disequazione impossibile
Nel caso non fosse possibile individuare dei valori reali che verificano la disequazione vuol dire che ci troviamo davanti ad una disequazione impossibile: l’insieme delle soluzioni corrisponde all’insieme vuoto: ( S = varnothing ).
Disequazione frazionaria
Le disequazioni frazionarie (o fratte) sono disequazioni che presentano uno o più termini con un’incognita al denominatore. Per identificare l’intervallo di soluzioni di questo tipo di espressioni è necessario procedere escludendo da questo insieme i valori che annullano il denominatore, ridurre le espressioni algebriche che la compongono ed effettuare uno studio del segno.Per ulteriori approfondimenti su (argomento) vedi anche qua
Per ulteriori approfondimenti sulle disequazioni fratte vedi anche qua
Intervallo delle soluzioni, tipologie e caratteristiche degli intervalli
L’insieme delle soluzioni di una disequazione è, in gran parte dei casi, un intervallo di valori. Gli insiemi delle soluzioni delle disequazioni possono essere insiemi infinitivi o finiti.Gli intervalli delle soluzioni individuate possono essere rappresentati sia numericamente, utilizzando gli insiemi, sia graficamente, sulla retta orientata. La retta orientata è una retta su cui è fissato un verso di percorrenza tramite una freccia. Su tale retta, che rappresenta i numeri reali, identifichiamo l’origine tramite lo zero e poniamo agli estremi della retta “meno infinito” e “più infinito”, seguendo l’orientamento dato dalla freccia. Questi due simboli servono a specificare che la retta è illimitata sia a destra che a sinistra dello zero.
Gli intervalli possono essere:
- limitati: sono rappresentati da segmenti
- illimitati: sono rappresentati da semirette o dall'intera retta orientata.
Per ulteriori approfondimenti sulle disequazioni fratte vedi anche qua
Intervalli limitati
Esaminiamo ora gli intervalli limitati; essi possono essere aperti, chiusi, o semichiusi, in base al fatto di contenere o meno i loro estremi. I valori compresi tra i due estremi dell’intervallo si dicono interni all’intervallo, mentre i numeri non compresi fra gli estremi si dicono esterni all’intervallo.
L’ampiezza dell’intervallo, se a e b sono gli estremi di tale intervallo, è data da b - a.
- Intervalli aperti Se indichiamo con a l’estremo inferiore e con b l’estremo superiore dell’intervallo, scrivendo i due valori tra parentesi tonde ( a ; b ) affermiamo che gli estremi non sono compresi nell’insieme delle soluzioni. Tale intervallo sarà composto dai numeri maggiori di a e minori di b, a e b esclusi.
- Intervalli chiusi Ponendo che gli estremi a e b siano sempre gli estremi del nostro intervallo, come nel caso precedente, utilizzando le parentesi quadre [ a ; b ] indichiamo che gli estremi del nostro intervallo sono compresi nell’insieme delle soluzioni. L’intervallo delle soluzioni sarà rappresentato quindi da tutti i numeri maggiori o uguali di a e minori o uguali di b.
- Intervalli semichiusi Un altro caso è quello degli intervalli semichiusi: insiemi in cui solo uno dei due estremi è compreso nell’intervallo delle soluzioni. Questi insiemi possono essere di due tipi:
- Intervalli chiusi a sinistra e aperti a destra Sono indicati con [ a ; b ) dove a è l’estremo compreso nell’intervallo, b è l’estremo non compreso. In questo caso l’insieme delle soluzioni sarà identificato da tutti i valori maggiori o uguali di a e strettamente minori di b.
- Intervalli chiusi a destra e aperti a sinistra Sono indicati con ( a ; b ]. In questo caso, differentemente dal precedente, a è l’estremo non compreso e b è l’estremo compreso nell’intervallo. L’insieme delle soluzioni è rappresentano quindi dai numeri strettamente maggiori di a e minori o uguali di b.
Intervalli illimitati
Gli intervalli illimitati possono essere costituiti da semirette, ed essere quindi aperti o chiusi, o dall'intera retta reale.
- Intervallo illimitato a destra e aperto a sinistra Gli intervalli di questo tipo si indicano con ( a ; +infty ). Tale insieme è costituito da tutti i numeri strettamente maggiori di a; l’estremo a non è incluso nell’insieme delle soluzioni.
- Intervallo illimitato a destra e chiuso a sinistra Gli intervalli di questo tipo vengono indicati con [ a ; +infty ). L’insieme delle soluzioni è costituito da tutti i numeri maggiori o uguali di a, a è perciò un estremo incluso.
- Intervallo illimitato a sinistra e aperto a destra Questo insieme si indica con ( -infty ; b ) ed costituito dai numeri strettamente minori di b; l’estremo b non è inclusi nell’insieme delle soluzioni.
- Intervallo illimitato a sinistra e chiuso a destra Questo caso si indica con ( -infty ; b ] e l’insieme delle soluzioni contenute in tale intervallo è rappresentato dai numeri minori o uguali di b, b è quindi un estremo incluso.
- Intervallo illimitato sia a sinistra che a destra Questo ultimo caso ( -infty ; +infty ) indica un intervallo di valori infinito, rappresenta quindi tutto l’insieme dei numeri reali.