Triangoli e criteri di congruenza

In questo appunto di geometria sono stati raggruppati i tre criteri di congruenza dei triangoli qualsiasi e i quattro criteri di congruenza dei triangoli rettangoli. La trattazione si apre con una breve panoramica sui triangoli, poi la loro classificazione in base ai lati e agli angoli e anche le definizioni di altezza mediana e bisettrice. Un richiamo alle proprietà dei punti notevoli e alla loro collocazione nel triangolo isoscele ed equilatero.

Generalità sui triangoli

Un triangolo è un insieme di punti del piano costituito da una poligonale chiusa di tre lati e dai suoi punti interni. Gli estremi dei tre lati si definiscono vertici del triangolo. Il vertice di un triangolo viene detto opposto a un lato quando non appartiene ad esso. Gli angoli che sono individuati da ogni coppia di lati sono definiti interni o semplicemente angoli. Gli angoli esterni di un triangolo sono quelli adiacenti agli angoli interni. Per ogni angolo interno ci sono due angoli esterni a esso corrispondenti.
Una prima classificazione dei triangoli può essere fatta in base ai lati.

• Triangolo isoscele: è un triangolo avente due lati congruenti;
• Triangolo equilatero: è un triangolo che ha tutti e tre i lati congruenti;
• Triangolo scaleno: è un triangolo che ha tutti i lati disuguali.

Nel triangolo isoscele, il punto comune ai lati congruenti si dice vertice, e l'angolo ad esso corrispondente di dice angolo al vertice. Il lato opposto a questo angolo si dice base, e gli angoli adiacenti ad essa si dicono angoli alla base. I lati congruenti del triangolo isoscele, per la loro posizione rispetto alla base, vengono anche chiamati lati obliqui.
Possiamo classificare i triangoli anche in base ai loro angoli:

• Un triangolo con tre angoli acuti si dice acutangolo;
• Un triangolo con un angolo ottuso si dice ottusangolo;
• Un triangolo con un angolo retto si dice rettangolo.

In un triangolo rettangolo, i lati adiacenti all'angolo retto si dicono cateti, mentre il lato opposto all'angolo retto si dice ipotenusa.

Altezza, mediana e bisettrice di un triangolo

In un triangolo qualsiasi, definiamo altezza il segmento perpendicolare condotto da un vertice alla retta del lato opposto. Questo lato prende il nome di base, e l'altezza si dice essere relativa a quel lato stesso.

In base al tipo di triangolo, l'altezza relativa ad un lato può essere interna, esterna al triangolo, o può coincidere con un lato:

In un triangolo vi sono tre altezze, una relativa a ciascuno dei tre lati, che si incontrano in un punto (che può essere interno o esterno, detto ortocentro del triangolo. Nel triangolo ottusangolo il punto è esterno, nel triangolo rettangolo l’ortocentro coincide con il vertice dell’angolo retto.

Mediana di un triangolo
In un triangolo qualunque, la mediana relativa ad un lato è il segmento che congiunge il vertice opposto a quel lato con il punto medio del lato stesso.

In un triangolo vi sono tre mediane che si incontrano in uno stesso punto detto baricentro.

Bisettrice di un triangolo
In un triangolo qualunque, definiamo bisettrice di un angolo il segmento, contenuto nella semiretta bisettrice di quell'angolo, che ha un estremo nel vertice dell'angolo, e l'altro estremo sul lato opposto.

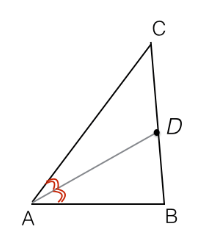
In un triangolo vi sono tre bisettrici che si incontrano in uno stesso punto detto incentro.
In un triangolo equilatero, le altezze, le mediane e le bisettrici coincidono, e i loro punti di incontro, detti punti notevoli (ortocentro, baricentro e incentro) si trovano nello stesso punto.

Criteri di congruenza

Due triangoli sono congruenti quando sono completamente sovrapponibili. Tuttavia esistono tre criteri, noti come criteri di congruenza dei triangoli, che permettono di stabilire la congruenza in modo più rapido, confrontando fra loro coppie di lati e coppie di angoli e non tutte le coppie di punti che si possono individuare nei due triangoli. I criteri mettono in relazione soltanto tre elementi del primo triangolo con i corrispondenti del secondo triangolo. Vediamo cosa affermano.

Primo criterio di congruenza

Due triangoli sono congruenti se hanno ordinatamente congruenti due lati e l’angolo tra essi compreso.

Utilizzando il primo criterio di congruenza si può dimostrare il teorema del triangolo isoscele in virtù del quale si stabilisce la congruenza dei due angoli alla base del triangolo. Nella dimostrazione del teorema, infatti, tracciando la bisettrice dell’angolo al vertice il triangolo isoscele viene diviso in due triangoli rettangoli dei quali si dimostra la congruenza applicando proprio il primo criterio.

Secondo criterio di congruenza

Due triangoli sono congruenti se hanno ordinatamente congruenti un lato e i due angoli ad esso adiacenti.

Terzo criterio di congruenza
Se due triangoli hanno ordinatamente congruenti i tre lati, allora essi sono congruenti.

Dai primi due criteri di congruenza derivano dunque alcune importanti conseguenze riguardanti i triangoli isosceli:

• In un triangolo isoscele gli angoli alla base sono congruenti;
• Un triangolo con due angoli congruenti è un triangolo isoscele che ha per base il lato adiacente ad essi.

I triangoli isosceli, inoltre, possiedono altre importanti proprietà:

• In un triangolo isoscele la bisettrice dell'angolo al vertice è pure altezza e mediana relativa alla base;
• In un triangolo isoscele la mediana relativa alla base è pure altezza e bisettrice dell'angolo al vertice;

Riportiamo per completezza anche il quarto criterio di congruenza detto anche secondo criterio generalizzato il cui enunciato è il seguente:
Due triangoli sono congruenti se hanno ordinatamente congruenti due angoli e un lato.

Osservazione

Negli enunciati dei criteri viene ripetuto sempre l’avverbio ordinatamente che significa nello stesso ordine. Perciò dobbiamo esprimere nell’ordine corretto gli elementi che si corrispondono nei due triangoli. Ad esempio, nella dimostrazione del primo criterio, se nel primo triangolo consideriamo il lati AB, AC, e l’angolo , nel secondo triangolo dobbiamo considerare nell’ordine A’B’, A’C’, è l’angolo , e questo vale per qualsiasi dimostrazione geometrica.

Criteri di congruenza dei triangoli rettangoli

Se due triangoli sono rettangoli, hanno senz’altro l’angolo retto congruente, pertanto è più facile stabilire se sono congruenti. In questo caso, oltre all’angolo retto, è sufficiente trovare altri due elementi che siano rispettivamente congruenti, e non tre come avviene per i triangoli in generale.
Per i triangoli rettangoli i criteri di congruenza sono quattro:
Primo: due triangoli rettangoli sono congruenti quando hanno rispettivamente congruenti due cateti.
I triangoli rettangoli in questo caso avendo congruenti due lati che sono i cateti e l’angolo fra essi compreso, ovvero l’angolo retto, risultano congruenti per il primo criterio di congruenza generale dei triangoli.
Secondo: due triangoli rettangoli sono congruenti quando hanno congruenti un angolo acuto e un cateto corrispondenti.
I triangoli rettangoli hanno congruenti l'angolo acuto, quello retto, e un lato (il cateto); sono perciò congruenti per il secondo criterio di congruenza generale dei triangoli.
Terzo: due triangoli rettangoli sono congruenti se hanno congruenti rispettivamente l’ipotenusa è un angolo acuto. I triangoli questa volta hanno congruenti due angoli, uno acuto e l’altro retto, e l’ipotenusa perciò sono congruenti ancora una volta per il secondo criterio di congruenza generale.
Quarto: due triangoli rettangoli sono congruenti se hanno congruenti rispettivamente l’ipotenusa e un cateto.

Per ulteriori approfondimenti sui triangoli e sulla congruenza vedi anche qui