Perchè le funzioni seno e coseno sono importanti
La trigonometria è la branca della matematica fondata sullo studio dei triangoli, con un focus particolare sui loro angoli. In questo ambito, concetti come le funzioni seno e coseno sono fondamentali, poiché permettono di giungere, a partire dagli angoli, alle misure dei lati della figura. Per questo motivo, tali formule sono un alleato importantissimo nella risoluzione di problemi ed esercizi. I valori delle funzioni seno e coseno di angoli con ampiezze "particolari" - come ad esempio- Gli angoli di [math]0°[/math]e[math]360°[/math]hanno rispettivamente[math]cos(a)=1[/math]e[math] sen(a)=0[/math]
- Gli angoli di [math]90°[/math]e[math]270°[/math]hanno rispettivamente[math]cos(a)=0[/math]e[math]sen(a)=1[/math]
- In generale, il valore del seno di un angolo è dato dalla proiezione del punto di intersezione tra una semiretta e la circonferenza goniometrica sull'asse delle ordinate.
- Per ottenere il coseno dell'angolo bisogna proiettare il punto di intersezione tra una semiretta dell'angolo e la circonferenza goniometrica sull'asse delle ascisse.
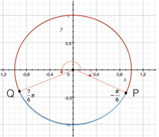
Questi valori derivano dallo studio della circonferenza goniometrica, ossia una circonferenza dal raggio unitario e centro fissato nell'origine del sistema cartesiano considerato. Lo strumento utilizzato per misurare l'ampiezza degli angoli - cioè il goniometro - non è altro che una circonferenza goniometrica.
Riconoscere il seno e il coseno dell'angolo è piuttosto semplice se si sfrutta quest'ultima analogia. Partiamo dalla definizione di angolo: esso non è altro che una parte di piano racchiusa tra due semirette aventi l'origine in comune, nonché vertice dell'angolo. L'estensione di tale spazio prende il nome di ampiezza.
Proprio come nelle misurazioni con il goniometro, per trovare l'ampiezza di un angolo, occorre allungare fino a toccare la circonferenza goniometrica la semiretta che non corrisponde all'asse delle ascisse. A questo punto è possibile definire il seno e il coseno dell'angolo misurato:
Ciò significa che se abbiamo un angolo con ampiezza nulla (0°), entrambe le semirette che lo definiscono coincidono con l'asse delle ascisse (asse x). In questo caso, quindi, il coseno corrisponde proprio alla lunghezza del raggio unitario e il seno è nullo.
D'altro canto, in un angolo di
Ovviamente, questo tipo di approccio non può essere esteso ad angoli con ampiezze intermedie, poiché risulterebbe complicato riconoscere il valore corretto delle proiezioni se questi sono diversi da 0 e da 1. Tuttavia esiste un metodo piuttosto intuitivo che può aiutarti a trovare i valori delle funzioni seno e coseno in presenza di determinati angoli: il metodo degli archi associati.
Cosa sono gli archi associati
Gli archi associati ci permettono di calcolare velocemente il seno e il coseno di alcuni angoli particolari, sfruttando le analogie con la geometria. Consideriamo, sulla circonferenza goniometrica, gli angoli

Dalla figura, possiamo dedurre che:

Ora, consideriamo i punti individuati dagli angoli complementari di misura

I punti intercettati da tali angoli sono simmetrici rispetto alla bisettrice del primo e del terzo quadrate, e pertanto hanno le coordinate scambiate.
Per gli archi complementari valgono le seguenti relazioni:

Questo approccio può essere esteso per ricavare un numero maggiore di formule: possiamo, infatti, applicare lo stesso ragionamento per tutti gli angoli complementari. Questi ultimi sono quelli che non si trovano nel primo quadrante, ma che hanno comunque somma

Ecco un esercizio per fissare le nozioni teoriche appena apprese: trovi la soluzione dell'esercizio nel forum di Matematicamente.it.
Esercizio proposto
Il complementare di un angolo è pari a un terzo del supplementare dello stesso angolo diminuito di due gradi. Trovare l'angolo.
per ulteriori approfondimenti sugli archi complementari e sulla trigonometria vedi anche qua