Disequazioni omogenee in (\sin x ) e ( cos x )
Vediamo alcuni esempi di equazioni omogenee in (\sin x) e (cos x); ricordiamo che per disequazione omogenea si intende una disequazione in cui tutti i termini sono dello stesso grado.Distinguiamo due casi, in cui il grado
Vediamo alcuni esempi in cui il grado n della disequazione è dispari.
Esempio: se il grado della disequazione è uno, ci troviamo di fronte ad una equazione lineare, che è anch'essa omogenea; consideriamo la seguente disequazione:
( \sqrt{3} \sin x - cos x gt 0 )
Possiamo determinare le soluzioni della disequazione per via grafica; in questo caso, dobbiamo fare un cambio di incognita, e poniamo:
( cos x = X ,,,, , ,,,, \sin x = Y )
Impostiamo poi un sistema per determinare i punti in cui la retta di equazione (\sqrt{3}Y - X = 0 ) interseca la circonferenza:
( \begin{cases}\sqrt{3}Y - X = 0 \ X^2 + Y^2 = 1 end{cases} )
Risolviamo il sistema e troviamo i punti di intersezione:
( \begin{cases} X = \sqrt{3}Y \ X^2 + Y^2 = 1 end{cases} \rightarrow \begin{cases} X = \sqrt{3} Y \ (\sqrt{3}Y)^2 + Y^2 = 1 end{cases} \rightarrow )
( \begin{cases} X = \sqrt{3}Y \ 3Y^2 + Y^2 = 1 end{cases} \rightarrow \begin{cases} X = \sqrt{3}Y \ 4Y^2 = 1 end{cases} \rightarrow )
( \begin{cases} X = \sqrt{3}Y \ Y^2 = frac{1}{4} end{cases} \rightarrow \begin{cases} X=\sqrt{3}Y \ Y = pmfrac{1}{2} end{cases} \rightarrow )
( Y = frac{1}{2} \rightarrow x = frac{\sqrt{3}}{2} )
( Y = -frac{1}{2} \rightarrow x = -frac{\sqrt{3}}{2} )
Il punto della circonferenza goniometrica che ha coordinate ((\sqrt{3}/2 ; 1/2 )) è l'estremo dell'arco cui corrisponde l'angolo (pi/6), mentre il punto che ha coordinate (( -\sqrt{3}/2 ; -1/2 )) è l'estremo dell'arco cui corrisponde l'angolo (7/6pi).
Ora, possiamo impostare il seguente sistema:
( \begin{cases} \sqrt{3}Y - X gt 0 \ X^2+Y^2 = 1 end{cases})
Possiamo determinare, in questo modo, gli archi della circonferenza che si trovano al di sopra della retta (\sqrt{3}Y - X = 0), e che sono quindi soluzioni della disequazione di partenza.
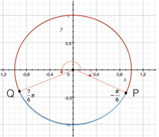
Rappresentiamo la situazione sulla circonferenza goniometrica:
Possiamo concludere che le soluzioni della disequazione sono date dagli angoli che appartengono al seguente intervallo:
( frac{pi}{6} + 2kpi lt x lt frac{7}{6} pi + 2k pi )
Esempio: Risolviamo la seguente disequazione di terzo grado:
( \sin^3 x + cos^3 x gt 0 )
Questa disequazione presenta al primo membro la somma di due cubi; ricordiamo che lo sviluppo della somma di due cubi è il seguente:
[ a^3 + b^3 = (a+b)(a^2+b^2-ab) ]
in particolare, abbiamo che il secondo fattore è positivo per qualunque valore di a e b; nel nostro caso, quindi, si ha:
( (\sin x + cos x)(\sin^2 x + cos^2 x - \sin x cos x) gt 0 )
Poiché il secondo fattore è sempre positivo, dobbiamo preoccuparci solo del primo; quindi, dobbiamo risolvere la seguente disequazione lineare:
( \sin x + cos x gt 0 )
Come abbiamo visto prima, possiamo fare un cambio di incognita ( (X = cos x) e (Y = \sin x) ) e impostare un sistema per determinare le zone della circonferenza goniometrica che si trovano al di sopra della retta di equazione (X + Y= 0):
( \begin{cases} X + Y gt 0 \ X^2 + Y^2 = 1 end{cases} )
Riportiamo la situazione sulla circonferenza goniometrica:
Possiamo concludere che le soluzioni della disequazione sono date dal seguente intervallo:
( -frac{pi}{4} + 2kpi lt x lt frac{3}{4} pi + 2kpi )
Esempio: Vediamo ora un esempio in cui il grado della disequazione è pari.
Consideriamo una disequazione omogenea di secondo grado:
( \sin^2 x + \sin x cos x lt 0 )
Procediamo con un raccoglimento a fattore comune:
( \sin x (\sin x + cos x) lt 0 )
In questo caso, si procede come per una normale disequazione di secondo grado; quindi, studiamo il segno di ciascun fattore, poi rappresentiamo la situazione sulla circonferenza goniometrica, dove studieremo il segno della disequazione.
Cominciamo studiando ( \sin x gt 0); gli intervalli della circonferenza che soddisfano questa disequazione sono tutti quelli che si trovano al di sopra dall'asse
( 2kpi lt x lt pi + 2kpi )
Poi, consideriamo la disequazione (\sin x + cos x gt 0); questa disequazione va risolta come una lineare, quindi impostiamo il sistema:
( \begin{cases} X + Y gt 0 \ X^2 + Y^2 = 1 end{cases} )
Svolgendo i calcoli, possiamo determinare le sue soluzioni:
( -frac{pi}{4} + 2kpi lt x lt frac{3}{4}pi + 2kpi )
Ora, riportiamo i precedenti intervalli in uno schema sulla circonferenza goniometrica, dove essi sono rappresentati con la linea colorata continua; procediamo poi con lo studio del segno.
Ricordiamoci che, poiché la disequazione di partenza è minore di zero, dobbiamo prendere gli intervalli con il segno meno.
Le soluzioni della disequazione sono quindi: ( -frac{pi}{4} + 2kpi lt x lt 2kpi vee frac{3}{4}pi + 2kpi lt x lt pi + 2kpi )
Che possiamo riassumere utilizzando la seguente scrittura: ( -frac{pi}{4} + kpi lt x lt kpi ).
