Equazioni goniometriche omogenee

di _stan

(320 punti)

9' di lettura

Equazioni omogenee in
[math] sin x [/math]
e
[math] cos x [/math]

Le equazioni goniometriche omogenee sono caratterizzate dal fatto che i loro termini sono tutti dello stesso grado.

Ad esempio, le equazioni lineari in

[math] sin x [/math]

[math] cos x [/math]

sono omogenee di primo grado; mentre, equazioni omogenee di secondo grado possono essere di questo tipo:

[math] \displaystyle a \cdot sin^2 x + b sin x cos x + c cos^2 x = 0 [/math]

Vediamo ora alcuni procedimenti che ci consentiranno di risolvere equazioni omogenee di grado n, distinguendo alcuni casi:

se nell'equazione presente il termine di grado
[math]n[/math]
in
[math] sin x [/math]
, cio se i valori
[math] x = \pi/2 + k\pi [/math]
non sono soluzioni, allora si dividono entrambi i membri dell'equazione per la potenza ennesima di
[math] cos x [/math]
(diverso da zero), ottenendo un'equazione di grado
[math]n[/math]
in
[math] \tan x [/math]
, equivalente all'equazione di partenza;
se nell'equazione presente il termine di grado
[math]n[/math]
in
[math] cos x [/math]
, cioè se i valori
[math] x = k\pi [/math]
non sono soluzione dell'equazione, si dividono entrambi i membri dell'equazione per la potenza ennesima di
[math] sin x [/math]
(diverso da zero), ottenendo un'equazione di grado
[math]n[/math]
in
[math] cot x [/math]
, equivalente all'equazione di partenza;
se nell'equazione non sono presenti le potenze ennesime in
[math] sin x [/math]
o in
[math] cos x [/math]
, si procede operando alcuni raccoglimenti a fattore comune.

Vediamo alcuni esempi:

Esempio: Risolviamo la seguente equazione omogenea:

[math] \displaystyle 2sin x cos x + sin^2 x = 0 [/math]

Questa equazione è di secondo grado, e compare il termine di secondo grado in

[math] sin x [/math]

; quindi, dividiamo entrambi i membri dell'equazione per

[math] cos x [/math]

al quadrato:

[math] \displaystyle \frac{2sin x cos x+sin^2 x}{cos^x} = 0 \rightarrow \frac{2sin x cos x}{cos^2}+\frac{sin^2 x}{cos x} = 0 [/math]

Semplificando, otteniamo:

[math] \displaystyle 2 \frac{sin x}{cos x} + \frac{sin^2 x}{cos^2 x} = 0 \rightarrow 2 \tan x + \tan^2 x = 0 [/math]

Quindi, abbiamo un'equazione equivalente di secondo grado in

[math] \tan x [/math]

; determiniamo le sue soluzioni:

[math] \displaystyle 2 \tan x + \tan^2 x = 0 \rightarrow \tan(2+\tan x) = 0 \rightarrow [/math]

[math] \displaystyle \rightarrow \tan x = 0 \vee \tan x = -2 [/math]

[math] \displaystyle \tan x = 0 \rightarrow x = k\pi [/math]

[math] \displaystyle \tan x = -2 \rightarrow x = arctan(-2) [/math]

Equazioni riducibili a omogenee

Spesso le equazioni che ci vengono proposte non sono immediatamente classificabili come omogenee, tuttavia, possiamo ricondurle ad esse attraverso alcuni passaggi.

Ad esempio, consideriamo la seguente equazione:

[math] \displaystyle a \cdot sin^2 x + b \cdot sin xcos x + c \cdot cos^2 x + d = 0 [/math]

Questa equazione non omogenea, in quanto compare il termine noto

[math]d[/math]

, che sappiamo essere di grado zero.

Possiamo, tuttavia, ricondurre questa equazione ad una omogenea di secondo grado moltiplicando il termine

[math]d[/math]

per

[math]1[/math]

, ricordando la relazione fondamentale della goniometria:

[math] \displaystyle sin^2 x + cos^2 x = 1 [/math]

Esempio: Risolviamo la seguente equazione riconducibile ad una omogenea:

[math] \displaystyle 2\sqrt{3}sin^2x - 3sin xcos x + 3cos^2x - \sqrt{3} = 0 [/math]

Moltiplichiamo il termine

[math]-\sqrt{3}[/math]

per

[math]1[/math]

[math] \displaystyle 2\sqrt{3}sin^2x - 3sin xcos x + 3cos^2 x - \sqrt{3} \cdot 1 = 0 [/math]

[math] \displaystyle 2\sqrt{3}sin^2x - 3sin xcos x + 3cos^2 x - \sqrt{3} \cdot (sin^2 x + cos^2 x) = 0 [/math]

[math] \displaystyle 2\sqrt{3}sin^2x - 3sin xcos x + 3cos^2 x - \sqrt{3}sin^2 x - \sqrt{3}cos^2 x = 0 [/math]

Svolgiamo i calcoli, e sommiamo i termini simili:

[math] \displaystyle \sqrt{3}sin^2 x - 3sin x cos x + (3-\sqrt{3}) cos^2 x = 0 [/math]

Procediamo risolvendo l'equazione omogenea; in questo caso, essendoci entrambi i termini si secondo grado, indifferente la scelta del divisore:

[math] \displaystyle \frac{\sqrt{3}sin^2 x - 3 sin x cos x + (3-\sqrt{3}) cos^2 x}{cos^2 x} = 0 [/math]

Otteniamo un'equazione equivalente di secondo grado in

[math] \tan x [/math]

[math] \displaystyle \sqrt{3}\tan^2 x - 3\tan x + 3 - \sqrt{3} = 0 [/math]

[math] \displaystyle \tan x = \frac{3\pm\sqrt{9-12\sqrt{3}+12}}{2\sqrt{3}} = \frac{3\pm\sqrt{21-12\sqrt{3}}}{2\sqrt{3}} [/math]

Otteniamo quindi (tramite le formule risolutive dei radicali doppi):

[math] \displaystyle \tan x = \frac{3\pm(2\sqrt{3}-3)}{2\sqrt{3}} = \begin{cases} \frac{3+2\sqrt{3}-3}{2\sqrt{3}} = 1 \\ \frac{3-2\sqrt{3}+3}{2\sqrt{3}} = \sqrt{3}-1 \end{cases} [/math]

Conoscendo i valori delle tangenti, possiamo ricavare il valore dellangolo

[math]x[/math]

[math] \displaystyle \tan x = 1 \rightarrow x = \frac{\pi}{4} + k\pi [/math]

[math] \displaystyle \tan x = \sqrt{3} - 1 \rightarrow x = arctan(\sqrt{3}-1) [/math]

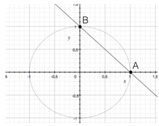
Risoluzione grafica di equazioni omogenee, o riconducibili a omogenee

Consideriamo un'equazione goniometrica omogenea di secondo grado del tipo:

[math] \displaystyle a \cdot sin^2 x + b \cdot sin x cos x + c \cdot cos^2 x + d = 0 [/math]

Ricordando le formule di duplicazione di seno e coseno, possiamo trasformare l'equazione in una equazione equivalente, lineare in

[math] sin 2x [/math]

[math] cos 2x [/math]

; ricordiamo le formule da utilizzare:

[math] \displaystyle sin^x = \frac{1-cos 2x}{2} \, \, \, \, , \, \, \, \, cos^2 x = \frac{1+cos 2x}{2} \, \, \, \, , \, \, \, \, sin xcos x = \frac{1}{2}sin 2x [/math]

Utilizzando queste relazioni, possiamo trasformare l'equazione omogenea di secondo grado nella seguente equazione:

[math] \displaystyle a \cdot \frac{1-cos 2x}{2} + b \frac{1}{2} sin 2x + c \frac{1-cos 2x}{2} + d = 0 [/math]

L'equazione, poi, può essere risolta per via grafica come abbiamo visto in precedenza per le equazioni lineari: si cercano le intersezioni della retta di equazione

[math]aX + bY + c[/math]

= 0 con la circonferenza goniometrica, essendo

[math] X = sin 2x [/math]

[math] Y = cos 2x [/math]

I punti trovati nel sistema rappresentano gli estremi degli archi cui corrispondono gli angoli che sono soluzioni dell'equazione di partenza.

Equazioni di secondo grado simmetriche in sen x e cos x

un'equazione si secondo grado simmetrica in sen x e cos x si presenta in questa forma:

[math] \displaystyle a sin x cos x + b (sin x + cos x) + c = 0 [/math]

e viene definita simmetrica perché non muta se si scambiano

[math] sin x [/math]

[math] cos x [/math]

Queste equazioni si possono risolvere ponendo

[math] x = y - \pi/4 [/math]

; sostituendo questa scrittura a

[math] sin x [/math]

[math] cos x [/math]

otteniamo:

[math] \displaystyle sin x = sin\Big(y - \frac{\pi}{4}\Big) = \frac{\sqrt{2}}{2}(sin y - cos y) [/math]

[math] \displaystyle cos x = cos\Big(y-\frac{\pi}{4}\Big) = \frac{\sqrt{2}}{2}(sin y + cos y) [/math]

Quindi, calcoliamo la somma e il prodotto di

[math] sin x [/math]

[math] cos x [/math]

[math] \displaystyle sin x + cos x = \frac{\sqrt{2}}{2}(sin y - cos y)+\frac{\sqrt{2}}{2}(sin x + cos y)= \sqrt{2}sin y [/math]

[math] \displaystyle sin x cos x = \frac{\sqrt{2}}{2}(sin y - cos y) \cdot \frac{\sqrt{2}}{2}(sin y + cos y)= [/math]

[math] \displaystyle =\frac{1}{2}(sin^2 y - cos^2 y) [/math]

Possiamo sostituire i valori trovati nell'equazione di partenza, e trasformare tutto in un'equazione si secondo grado in (sin y), che può essere facilmente risolta:

[math] \displaystyle a \cdot \frac{1}{2} (sin^2 y - cos^2 y) + b \sqrt{2}sin y + c = 0 [/math]

[math] \displaystyle \frac{a}{2} (2sin^2 y - 1) + b \sqrt{2} sin y + c = 0 [/math]

Da cui otteniamo:

[math] \displaystyle asin^2 y + b \sqrt{2} sin y + c - \frac{a}{2} = 0 [/math]