La circonferenza goniometrica
Il concetto di funzione trigonometria di seno e coseno nasce a partire dalla circonferenza goniometrica.Consideriamo, in un sistema di riferimento cartesiano, una circonferenza avente come centro l'origine degli assi
La figura 1 mostra la circonferenza goniometrica.

Definizioni
Di seguito, alcune definizioni:- Il punto A, di coordinate [math](0; 1)[/math], è definito come origine degli archi.
- Gli angoli che consideriamo appartenenti alla circonferenza goniometrica sono rappresentati sulla circonferenza in modo tale da avere un lato coincidente con l'asse delle ascisse, e l'altro che interseca la circonferenza in un punto P.
- Sapendo che l'ampiezza di un angolo in radianti è uguale alla lunghezza dell'arco corrispondente divisa per il raggio della circonferenza, e sapendo anche che il raggio della circonferenza goniometrica è pari a 1, possiamo affermare che le lunghezze degli archi della circonferenza rappresentano le ampiezze in radiant dei rispettivi angoli.
Angoli nella circonferenza goniometrica
Avendo visto che le lunghezze degli archi della circonferenza sono le ampiezze in radianti degli archi, adesso andiamo a rappresentare sulla circonferenza i principali angoli(Figura 2):

Sono stati rappresentati diversi angoli, tra cui:
- Angolo [math] 0°[/math], ovvero[math]0 [/math]Radianti;
- Angolo [math] 45°[/math], ovvero[math]\frac{π}{4} [/math]Radianti;
- Angolo [math] 90°[/math], ovvero[math]\frac{π}{2}[/math]Radianti;
- Angolo [math] 180°[/math], ovvero[math]π [/math]Radianti;
- Angolo [math] 270°[/math], ovvero[math]\frac{3π}{2} [/math]Radianti;
- Angolo [math] 360°[/math], ovvero[math]2π [/math]Radianti;
Le funzioni seno e coseno
Per ogni angoloDa qui si può andare quindi a scrivere le coordinate del punto P come segue:
Poiché la circonferenza goniometrica ha raggio 1, il seno e il coseno di un angolo sono sempre minori di 1, e maggiori di -1. Ovvero il campo di esistenza delle funzioni seno e coseno sarà l'intervallo
In particolare, sapendo che la circonferenza goniometrica ha centro in
da cui, possiamo ricavare la seguente relazione, che viene definita prima relazione fondamentale della goniometria:
Possiamo determinare seno e coseno degli angoli principali applicando il teorema di Pitagora ai triangoli rettangoli individuati dai segmenti

Periodicità delle funzioni seno e coseno
Le funzioni seno e coseno vengono definite funzioni periodiche; infatti, possiamo notare che i valori che esse assumono nell'intervalloRiassumendo, possiamo semplicemente scrivere:
Sinusoide e cosinusoide
Le funzioni seno e coseno possono essere rappresentate nel piano cartesiano come vere e proprie funzioni; per tracciare i lori grafici, si comincia tracciando il grafico della funzione in un piccolo intervallo, poi, sfruttando la periodicità della funzione stessa, si può tracciare la funzione su tutto l'asse reale.

Consideriamo la funzione
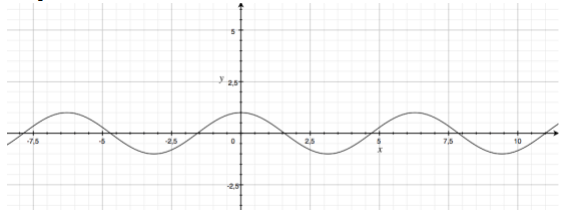
La funzione
Allo stesso modo, possiamo tracciare il grafico della funzione

Sapendo che la funzione è periodica, possiamo tracciare il grafico completo:

La funzione
Altro materiale di supporto
Guarda la videolezione: "Le relazioni fondamentali della goniometria" sul sito delle lezioni di Matematicamente.it.Consulta il Formulario delle funzioni goniometriche a cura di Gianni Sammito.



