Risoluzione dei triangoli rettangoli

Un prezioso appunto di trigonometria molto esaustivo, contenente un riepilogo completo delle formule per la risoluzione dei triangoli rettangoli. Dopo il ripasso degli enunciati dei vari teoremi, si passa alla loro applicazione per la risoluzione dei triangoli rettangoli esaminando i 4 casi. Vedremo poi come si determina l'area di un triangolo con la trigonometria e anche il teorema della corda.

Teoremi sui triangoli rettangoli

Molti problemi che hanno a vedere con la fisica, l’astronomia, la topografia, e altre scienze portano spesso a dover lavorare con triangoli dei quali si conoscono solo alcuni elementi e se ne vogliono trovare altri. Ad esempio, è possibile calcolare l’altezza di una torre se possiamo misurare la lunghezza della sua ombra proiettata al suolo e l’inclinazione dei raggi solari. La trigonometria ci fornisce gli strumenti per studiare le relazioni che intercorrono tra i lati e gli angoli di un triangolo, in questo modo sarà possibile risolvere anche i problemi del tipo di quello proposto. I teoremi che illustreremo ci permetteranno di determinare lati o angoli di triangoli rettangoli, conoscendo altri dati su di essi, ad esempio altri lati o altri angoli, sfruttando le funzioni goniometriche applicate a tali angoli.

Un triangolo rettangolo per definizione ha un angolo retto perciò basta conoscere sono due elementi perché il terzo è sempre quest’angolo. Possono essere noti un lato e due angoli, due lati e l’angolo fra essi compreso, due lati e un angolo opposto a uno di essi, oppure i tre lati. Esaminiamo allora i quattro casi possibili singolarmente. Consideriamo il triangolo rettangolo HOP, rettangolo Nel vertice H, rappresentato in figura, i cui lati hanno misure a, b, c, Abbiamo le seguenti relazioni tra lati e funzioni goniometriche:

• [math]b=a \cdot sin \beta = a\cdot cos \gamma[/math]
• [math]c=a \cdot cos \beta = a\cdot sin \gamma[/math]

Vale il seguente Teorema 1:
in ogni triangolo rettangolo, la misura di un cateto è uguale al prodotto tra la misura dell'ipotenusa e il coseno dell'angolo acuto a esso adiacente, o il seno dell'angolo opposto. Questa relazione ci permette, poi, di ricavare l'ipotenusa in funzione di un cateto e di un angolo; in particolare si ha:

• [math]a=\frac{b}{sin\beta}=\frac{b}{cos \gamma}[/math]
• [math]a=\frac{c}{cos\beta}=\frac{c}{sin \gamma}[/math]

Ne deriva che:

in ogni triangolo rettangolo, la misura dell'ipotenusa è uguale al rapporto tra la misura di un cateto e il coseno dell'angolo adiacente (al cateto) o al seno dell'angolo opposto (al cateto).

Possiamo inoltre utilizzare le formule appena viste per ricavare altre relazioni tra i lati di un triangolo rettangolo e la tangente o la cotangente dei suoi angoli. Vediamo allora il teorema successivo.

Teorema 2: In ogni triangolo rettangolo la misura di un cateto è uguale a quella dell'altro cateto moltiplicata per la tangentedell'angolo opposto al primo cateto, oppure per la cotangente dell'angolo acuto a esso adiacente. In simboli:

• [math]b=c \cdot tan \beta = c \cdot cot \gamma[/math]
• [math]c=b \cdot cot \beta = b \cdot tan \gamma[/math]

Risoluzione dei triangoli rettangoli

Risolvere un triangolo rettangolo significa determinare le misure dei suoi elementi, cioè le misure dei suoi lati, e le ampiezze dei suoi angoli. Utilizzando i teoremi visti in precedenza, possiamo risolvere facilmente un triangolo rettangolo, se ci troviamo in uno dei seguenti casi:

Caso 1
Sono noti l'ipotenusa OP e l'angolo acuto

. In questo caso, possiamo determinare l'angolo restante, sapendo che in un triangolo rettangolo la somma dei due angoli acuti e 90° perché questi due sono complementari inoltre, per i teoremi visti in precedenza, possiamo ricavare le misure degli altri lati:

• [math]\gamma=90°-\beta[/math]
• [math]\overline{PH}=\overline{PO} \cdot sin \beta[/math]
• [math]\overline{OH}=\overline{PO} \cdot cos \beta[/math]

Caso 2
Sono noti il cateto PH e l'angolo acuto adiacente

.
Possiamo determinare l'angolo restante come in precedenza, e gli altri elementi sfruttando i teoremi sui triangoli rettangoli in questo modo:

• [math]\beta=90°-\gamma[/math]
• [math]\overline{PO}=\frac{\overline{PH}}{cos \gamma}[/math]
• [math]\overline{OH}=\overline{PH} \cdot tan \gamma[/math]

Caso 3
Sono note le misure dell'ipotenusa PO e di un cateto, per esempio PH. Possiamo ricavare il coseno dell'angolo adiacente al cateto, che equivale al seno dell'angolo ad esso opposto; poi, possiamo determinare l'altro cateto con il teorema di Pitagora:

• [math]sin \beta = cos \gamma =\frac{\overline{PH}}{\overline{PO}}[/math]
• [math]\overline{OH}=\sqrt{\overline{PO}^2-\overline{PH}^2}[/math]

Caso 4
Sono note le misure dei due cateti PH e OH. In questo caso, possiamo utilizzare il secondo teorema per ricavare le funzioni goniometriche dei due angoli adiacenti ai cateti; per l'ipotenusa, possiamo sfruttare il teorema di Pitagora:

• [math]tan \beta = cot \gamma =\frac{\overline{PH}}{\overline{OH}}[/math]
• [math]\overline{PH}=\sqrt{\overline{PH}^2-\overline{OH}^2}[/math]

Area di un triangolo

Consideriamo un triangolo ABC qualunque, del quale conosciamo due lati e l'angolo tra essi compreso; il seguente teorema ci permette di determinare l'area del triangolo:

Teorema 3: l'area di un triangolo è uguale al semiprodotto di due lati per il seno dell'angolo tra essi compreso.

Teorema della corda

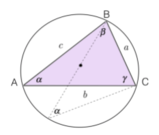
Consideriamo una circonferenza di raggio r e una sua corda AB; il teorema sfrutta il fatto che gli angoli alla circonferenza che insistono sullo stesso arco, e quindi che sono descritti da una stessa corda, sono tutti congruenti fra loro.

Enunciato del teorema della corda: La lunghezza di una corda di una circonferenza è uguale al prodotto del diametro per il seno di uno qualunque degli angoli alla circonferenza che insistono su uno dei due archi determinati dalla corda stessa. In simboli:

Per ulteriori approfondimenti sulla risoluzione dei triangoli rettangoli vedi anche qui