_stan
di _stan
(320 punti)
6' di lettura

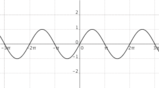
Continuità di sen x e cos x

Le funzioni sen x e cos x sono continue per ogni x reale, quindi possiamo scrivere:

[math] \displaystyle\lim_{x \rightarrow c} \sin (x) = \sin (c) \, \, \, \, \, \, \, \, \, \forall c \in \mathbb{R} [/math]

[math] \displaystyle\lim_{x \rightarrow c} \cos (x) = \cos (c) \, \, \, \, \, \, \, \, \, \forall c \in \mathbb{R} [/math]

Esempio: Calcoliamo il limite:

[math] \displaystyle\lim_{x \rightarrow \frac{\pi}{2}} (x \cdot \sin x \cos x) [/math]

Sappiamo che il limite del prodotto di funzioni uguale al prodotto di dei limiti delle funzioni stesse, quindi:

[math] \displaystyle\lim_{x \rightarrow \frac{\pi}{2}} (x \cdot \sin x \cos x) = \lim_{x \rightarrow \frac{\pi}{2} } x \cdot \lim_{x \rightarrow \frac{pi}{2}} \sin x \cdot \lim_{x \rightarrow \frac{\pi}{2}} \cos x [/math]

E, poiché tutte le funzioni che compaiono sono continue, il limite per

[math]x \to \frac{\pi}{2}[/math]
di ciascuna funzione equivale al valore che la funzione stessa assume per
[math]x = \frac{\pi}{2}[/math]
:

[math] \displaystyle\lim_{x \rightarrow \frac{\pi}{2}} x = \frac{\pi}{2} \, \, \, \, \,\lim_{x \rightarrow \frac{\pi}{2}} \sin x = \sin \frac{\pi}{2} = 1 \,, \, \, \,\lim_{x \rightarrow \frac{\pi}{2}} \cos x = \cos\frac{\pi}{2} = 0 [/math]

Di conseguenza, il limite di partenza dato da:

[math] \displaystyle\lim_{x \rightarrow \frac{\pi}{2}} (x \cdot \sin x \cos x) = \frac{\pi}{2} \cdot 1 \cdot 0 = 0 [/math]

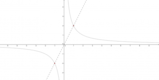
Continuità delle funzioni tg x e ctg x

Abbiamo appena visto che le funzioni sen x e cos x sono continue per ogni x reale; sappiamo, inoltre, che se due funzioni sono continue in un certo intervallo I, anche il loro rapporto è una funzione continua in I, nei punti che non annullano il denominatore della frazione.

Con queste premesse, possiamo affermare che anche la funzione tangente, che è data dal rapporto di sen x e cos x, è una funzione continua in tutto R, esclusi i valori che annullano cos x; è quindi, una funzione continua nel suo dominio:

[math] \displaystyle\lim_{x \rightarrow c} \tan (x) = \lim_{x \rightarrow c} \frac{\sin(x)}{\cos(x)} = \frac{\sin(c)}{\cos(c)} \, \, \, \, \,, \,\,\, \forall x \ne \frac{\pi}{2} + k\pi [/math]

Un discorso analogo può essere fatto per la funzione cotangente, in quanto rapporto di cos x e sen x; anch'essa è continua in tutto il suo dominio, cioé in R tranne i valori che annullano sen x:

[math] \displaystyle \lim_{x \rightarrow c} \cot (x) = \lim_{x \rightarrow c} \frac{\cos(x)}{\sin(x)} = \frac{\cos(c)}{\sin(c)} \,\,\,\, \, ,\,\,\, \forall x \ne k\pi [/math]

Continuità del valore assoluto di una funzione

Il limite del valore assoluto di una funzione equivale al valore assoluto del limite della funzione stessa.

Quindi, se una funzione f(x) è continua in un punto c, o in un intervallo I, anche la funzione valore assoluto, di equazione y = |f(x)| è continua in c, o in I, infatti, si ha che:

[math] \displaystyle \lim_{x \rightarrow c} f(x) = f(c) = l R\rightarrow \lim_{x \rightarrow c} |f(x)| = |f(c)| = |l| [/math]

Limite e continuità della radice di una funzione

Teorema: Se una funzione f(x) tende ad un limite l, maggiore di zero, allora la funzione radice ennesima di f(x) tende alla radice ennesima di l, per ogni n positivo:

[math] \displaystyle \lim_{x \rightarrow c} f(x) = l \, \, \, \,, \, \, \, \, \, l \gt 0 R\rightarrow \lim_{x \rightarrow c} \sqrt[n]{f(x)} = \sqrt[n]{l}\,\,\,\, \, \,\,\,\, n \in \mathbb{N_0} [/math]

Nel caso, invece, in cui il limite l sia negativo, il teorema valido solo nel caso in cui n sia dispari.

Esempio: Calcoliamo il limite della seguente funzione, per x che tende a 1, per difetto:

[math] \displaystyle\lim_{x \rightarrow 1^{-}} \sqrt[4]{1-x^2} [/math]

Sappiamo che il limite di una radice quarta equivale alla radice quarta del limite del radicando, quindi abbiamo che:

[math] \displaystyle\lim_{x \rightarrow 1^{-}} \sqrt[4]{1-x^2} = \sqrt[4]{\lim_{x\rightarrow 1^{-}} (1 - x^2)} [/math]

Il radicando è un polinomio in x, ed è quindi una funzione continua; sappiamo che, nel caso di funzioni continue, il limite per x che tende ad un valore finito coincide con il valore che la funzione assume nel punto, quindi abbiamo che:

[math] \displaystyle\lim_{x \rightarrow 1^{-}} (1 - x^2) = 1 - (1^{-})^2 = 1 - 1 = 0 [/math]

Notiamo che, è possibile calcolare il limite della funzione in quanto, poiché il radicando della funzione risulta maggiore o uguale a zero per valori di x tali che

[math] -1 \le x \le 1, la funzione [math] f(x) = 1 - x^2 [/math]
risulta maggiore di zero in un intorno sinistro di 1.

A questo punto, possiamo concludere che la funzione di partenza tende proprio a zero, in quanto la radice quarta di zero è zero:

[math] \displaystyle \lim_{x \rightarrow 1^{-}} \sqrt[4]{1-x^2} = \sqrt[4]{0} = 0 [/math]

Se volessimo determinare l'insieme di continuità della funzione precedente, non dobbiamo far altro che determinare il dominio della funzione; infatti, sappiamo che il radicando, essendo un polinomio, una funzione continua per ogni x, mentre la funzione radice quarta una funzione continua per ogni x appartenente al dominio.

Calcoliamo quindi il dominio della funzione:

[math] 1 - x^2 \ge 0 \rightarrow -1 \le x \le 1 [/math]

La funzione, quindi, risulta essere continua per ogni x appartenente all'intervallo [ -1; 1 ] .

Vuoi approfondire Analisi Matematica – Esercizi, problemi e formule di Analisi Matematica con un insegnante esperto?
Trovalo su Ripetizioni.it