_stan
di _stan
(320 punti)
6' di lettura

Consideriamo la funzione seguente:

[math] y = f(x) = x^3 [/math]

Sappiamo che essa definita per ogni x reale, quindi esaminiamo il comportamento della funzione mano a mano che i valori di x, positivi o negativi, diventano molto grandi, in valore assoluto.

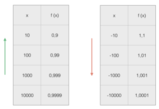
Riassumiamo in uno schema i valori assunti da f(x) al variare di x:

Possiamo quindi notare che, all'aumentare di x, la funzione f(x) assume valori sempre pi grandi, quindi, possiamo scrivere che per

[math]{x}\rightarrow+\infty, f{{\left({x}\right)}}\rightarrow+\infty[/math]
; allo stesso modo, al diminuire di x, f(x) assume valori sempre pi piccoli, quindi per
[math]{x}\rightarrow-\infty, f{{\left({x}\right)}}\rightarrow-\infty[/math]
.

In termini generali, si ha che:

[math] \lim_{x \rightarrow \infty} f(x) = \infty [/math]

Diamo ora una definizione generale, considerando una generica funzione f(x), definita in un intorno di infinito.

Definizione di limite infinito

Si dice che, per x tendente all'infinito, la funzione y=f(x) ha per limite infinito, e si scrive

[math] \lim_{x \rightarrow \infty} f(x) = \infty [/math]

se, comunque si scelga un numero positivo M, arbitrariamente grande, si può determinare, in corrispondenza di esso, un introno di infinito tale che, per ogni x di tale intorno, si ha:

[math] | f(x) | \gt M [/math]

cioè, ricordando le proprietà del valore assoluto:

[math] f(x) \lt -M \vee f(x) \gt M [/math]

Quindi, possiamo dire che, in corrispondenza di un qualunque M > 0 possibile determinare un intorno di infinito tale che, per ogni x di questo intorno, i corrispondenti punti di f(x) giacciono all'esterno della linea striscia delimitata dalle rette y = M e y = -M.

Per verificare un limite infinito per x che tende all'infinito occorrer risolvere la disequazione | f (x) | > M, e accertarsi che l'insieme delle soluzioni trovate contenga un intorno di infinito.

Esempio di verifica di un limite infinito

Verifichiamo il seguente limite:

[math]lim_{x \rightarrow \infty} \log(1 + x^2) = \infty [/math]

Dobbiamo verificare che, comunque scelto un M > 0, arbitrariamente grande, la disequazione |f(x)| > M contenga un intorno di infinito.

Risolviamo, quindi, la seguente disequazione:

[math]| \log(1+x^2) | \gt M[/math]

[math]\log(1+x^2) \lt -M \vee \log(1+x^2) \gt M[/math]

Cominciamo risolvendo la prima disequazione:

[math]\log(1+x^2) \lt -M \rightarrow 1+x^2 \lt e^{-M} \rightarrow -\sqrt{e^{-M} – 1} \lt x \lt \sqrt{e^{-M}-1}[/math]

Risolviamo ora la seconda:

[math]\log(1+x^2) \gt M \rightarrow 1+x^2 \gt e^M \rightarrow x \lt – \sqrt{e^M – 1} \vee x \gt \sqrt{e^{-M} – 1}[/math]

Le soluzioni della disequazione di partenza sono date dall'unione delle soluzioni delle due disequazioni, quindi abbiamo il seguente intervallo:

[math](-\infty; -\sqrt{e^M-1}) \cup (-\sqrt{e^{-M}-1}; \sqrt{e^M-1}; +\infty)[/math]

L'intervallo delle soluzioni contiene un intorno di infinito (dato dalle soluzioni della seconda disequazione ), pertanto possiamo affermare che il limite di partenza verificato.

In alcuni casi, la funzione po tendere solo a

[math]+\infty[/math]
, o solo a
[math]-\infty[/math]
. In particolare, se comunque si scelga M > 0, arbitrariamente grande, possibile determinare un intorno di infinito per cui sia verificata la disequazione f(x) [math]{x}\rightarrow \infty[/math],
[math]f{{\left({x}\right)}}\rightarrow-\infty[/math]
:

[math]\lim_{x \rightarrow \infty} f(x) = -\infty[/math]

Allo stesso modo, se comunque si scelga M > 0, si può trovare un intorno di

[math]\infty[/math]
in cui valga f(x) > M, allora per
[math]{x}\rightarrow \infty[/math]
,
[math]f{{\left({x}\right)}}\rightarrow+\infty[/math]
:

[math]\lim_{x \rightarrow \infty} f(x) = +\infty[/math]

Se, invece, le disequazioni f(x) M sono verificate solo in un intorno di meno infinito, o solo in un intorno di pi infinito, si dice che per x tendente a più infinito

[math]({x}\rightarrow +\infty)[/math]
, oppure per x tendente a meno infinito
[math]({x}\rightarrow -\infty)[/math]
, f(x) ha per limite
[math]\infty[/math]
( o, rispettivamente,
[math]+\infty[/math]
, o
[math]-\infty[/math]
).

Esempio di verifica di un limite infinito per x tendente all'infinito

Verificare il seguente limite infinito, per x tendente a infinito:

[math]\lim_{x \rightarrow +\infty} (1 – \sqrt{x}) = -\infty[/math]

Vogliamo verificare che, comunque scelto un M > 0, abbastanza grande, esista un intorno di pi infinito in cui sia verificata la disequazione f(x) [math]-\infty[/math]. Quindi, impostiamo la seguente disequazione:

[math]1 – \sqrt{x} \lt -M[/math]

Risolviamo la disequazione:

[math]1-\sqrt{x}\lt -M \rightarrow \sqrt{x} \gt M + 1 \rightarrow x \gt (M + 1)^2[/math]

La soluzione della disequazione può anche essere scritta come intervallo, in questo modo:

[math]\Big((M+1)^2; +\infty\Big)[/math]

Che rappresenta proprio un intorno di

[math]+\infty[/math]
, quindi il limite di partenza stato verificato.
Vuoi approfondire Analisi Matematica – Esercizi, problemi e formule di Analisi Matematica con un insegnante esperto?
Trovalo su Ripetizioni.it