Lo spazio campionario per un esperimento è l’insieme di tutti i suoi possibili esiti. Per esempio, se l’esperimento è il lancio di due di dadi e si rappresentano le coppie di numeri che escono sulle facce superiori, {5, 2} è un possibile esito e appartiene allo spazio campionario, ma {1, 7}, {-4, 3}, {4, 4, 4}, {a, 1} e {3/4, 3/4} non sono esiti possibili.
Sia S uno * spazio campionario * di eventi. Siano A e B eventi in S.
Sia P(A) la probabilità dell’evento A. Allora:
Due eventi sono mutualmente esclusivi se essi non possono accadere contemporaneamente. Per esempio, gli eventi estrai una figura e estrai picche non sono mutualmente esclusivi, dal momento che possiamo estrarre il re di picche, ma gli eventi estrai una carta rossa e estrai picche sono mutualmente esclusivi.
Sia f la frequenza di un evento A e n sia la dimensione del campione. La probabilità dell’evento A è
In una scuola superiore, viene selezionato un campione di 500 studenti e 392 di questi studenti sanno usare il computer. Qual è la probabilità che uno studente scelto a caso dal campione sappia usare il computer
La probabilità è la frequenza relativa degli studenti nel campione che sanno usare il computer rispetto al numero degli studenti del campione :
Sono lanciate tre monete. Calcola la probabilità che esca testa esattamente una volta.
Calcola la probabilità di vincere una lotteria se la combinazione vincente è formata da sei numeri estratti a caso dai numeri da 1 a 49.
Lo spazio campionario degli esiti ugualmente probabili è il numero di combinazioni di 49 numeri presi 6 alla volta. Solamente una combinazione può essere quella vincente.
La dimensione dello spazio campionario si trova usando la formula per le combinazioni:
La probabilità di essere colpito da un fulmine è maggiore di quella di vincere tale lotteria.
Basandosi sui dati I.S.T.A.T 20 contribuenti scelti da un campione di 750, che hanno dichiarato un reddito inferiore a £ 20000000, subiscono una verifica ogni anno. Calcola la probabilità di una revisione se il reddito riportato è inferiore a £20000000.
P(A o B) = P(A) + P(B) – P(A e B)
Due eventi sono detti indipendenti se l’occorrenza di uno di essi non ha effetti sulla probabilità del verificarsi dell’altro.
Lancia due dadi. Qual è la probabilità di avere un 6 sul primo dado E un 6 sul secondo dado? Qual è la probabilità di ottenere un 6 sul primo dado O un 6 sul secondo dado?
Poiché gli esiti dei due dadi sono eventi indipendenti, la probabilità di avere un 6 sul primo dado e un 6 sul secondo dado, per la regola della moltiplicazione, è
la probabilità di ottenere un 6 sul primo dado o un 6 sul secondo dado, per la regola di addizione, è
Si estrae una carta da un mazzo di 52 carte da gioco. Qual è la probabilità che la carta sia di fiori OPPURE una figura?
Sia A l’evento di estrarre una carta di fiori e B sia l’evento di estrarre una figura.
Ci sono 13 fiori, così P(A) = .
Tre carte — fante, donna e re di fiori — sono contemporaneamente fiori e figure. Così P(A e B)= .
Per la regola dell’addizione, la probabilità di estrarre una carta di fiori o una figura è
Se la probabilità che nevichi il Martedì è 0.3 e la probabilità che nevichi il Venerdì è 0.9, qual è la probabilità che nevichi sia il Martedì che il Venerdì?
Se supponiamo che l’eventualità che nevichi in un dato giorno sia un evento indipendente, la probabilità che nevichi sia il Martedì che il Venerdì è il prodotto delle probabilità.
Siano A e B eventi in uno spazio di probabilità. La probabilità condizionata di A, dato che l’evento B è accaduto, è denotata con P(A|B) . Vale la relazione
Siano A 1 , A 2 … A n eventi mutualmente esclusivi la cui unione sia uno spazio campionario S. Sia E un evento arbitrario di S tale che . Allora
P(A 1 |E) = P(A 1 )*P(E|A 1 )/(P(A 1 )*P(E|A 1 ) + P(A 2 )*P(E|A 2 ) + … +P(A n )*P(E|A n ))
Lancia un dado rosso e un dado verde. Dato che la somma dei dadi è minore di 4, qual è la probabilità che il dado verde sia 1 ?
Rappresentiamo con (g, r) l’esito sul dado verde e sul dado rosso. La dimensione dello spazio campionario è 36. L’evento somma dei dadi minore di 4 è costituito da
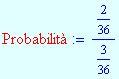
In una famiglia con due figli è noto che c’è almeno un maschio. Qual è la probabilità che entrambi i figli siano masch i ?
Lo spazio degli eventi è { MM, MF, FM, FF }. La probabilità che ci sia almeno un maschio . La probabilità che entrambi i figli siano maschi è
. La probabilità che entrambi i figli siano maschi sapendo che già uno sia almeno un maschio è :
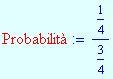
In una classe universitaria di matematica, il 5% degli uomini e il 2% delle donne hanno più di 22 anni. Il 70% degli studenti nella classe sono donne. Se uno studente scelto a caso ha più di 22 anni, qual è la probabilità che lo studente sia una donna ?
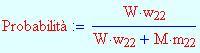

ottimo per chi non è un esperto!