Ricerca dei punti di massimo, minimo e flessi

Il metodo delle derivate successive permette di studiare e di determinare gli estremi relativi di una funzione. Per utilizzare questo metodo, che non prevede lo svolgimento di disequazioni, è necessario che la funzione sia derivabile due volte con continuità (questo termine si usa, in genere, per indicare che la derivata n-esima di una funzione sia continua).

Teorema: Sia

una funzione derivabile due volte, con derivata seconda continua, nei punti interni di un intervallo , e sia un punto interno di tale intervallo; allora, si ha che:

1. Se risulta
   [math]f'(c) = 0[/math]
   e (f''(c) lt 0), allora
   [math]c[/math]
   è un punto di massimo relativo;
2. Se risulta
   [math]f'(c) = 0[/math]
   e (f''(c) gt 0), allora
   [math]c[/math]
   è un punto di minimo relativo.

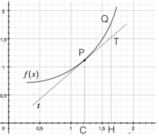
Notiamo che il teorema può essere interpretato per via grafica: infatti, nel primo caso, abbiamo nel punto c una tangente orizzontale, e poiché la derivata seconda in quel punto è negativa, la curva volge la concavità verso in basso; al contrario, nel secondo caso, in cui la derivata seconda è positiva, la curva volge la concavità verso l'alto.

In alcuni casi, però, come accade per esempio con la funzione

, o , che sia la derivata prima che la derivata seconda sono nulle (in questo caso nell'origine). Nel primo caso, la funzione presenta nell'origine un punto di minimo, mentre la seconda un flesso.

Il teorema appena mostrato, quindi, fornisce una condizione sufficiente per l'esistenza di un estremo relativo, ma non necessaria.

Metodo della derivata terza

Il metodo della derivata terza fornisce un criterio sufficiente per la determinazione dei punti di flesso a tangente orizzontale.

Teorema: Sia

una funzione derivabile tre volte, con derivata terza continua, nei punti interni di un intervallo . Se è un punto interno a , e si ha che:

[ f'(c) = f''(c) = 0 wedge f'''(c)
e 0 ]

allora,

è un punto di flesso a tangente orizzontale. In particolare, il flesso sarà ascendente se (f'''(c) gt 0), e discendente se (f'''(c) lt 0).

Nel caso in cui, invece, la derivata seconda della funzione, calcolata in

, è nulla, ma sono diverse da zero la derivata prima e la derivata terza, cioè se:

[ f''(c) = 0 wedge f'(c)
e 0 wedge f'''(c)
e 0 ]

allora, il punto

rappresenta un punto di flesso a tangente obliqua.

Generalizzazione del metodo delle derivate successive:

Possiamo riassumere i metodi appena visti per la determinazione dei punti di massimo, minimo e flesso di una funzione con un unico teorema.

Teorema: Sia

una funzione derivabile volte con derivata - esima continua nei punti interni di un intervallo . Sia un punto interno di , in cui si ha che:

[ f'(c) = f''(c) = ldots = f^{(n-1)}(c) = 0 wedge f^{(n)}(c)
e 0 ]

possiamo affermare che:

• se
  [math]n[/math]
  è pari, il punto
  [math]c[/math]
  risulta essere un punto estremante; in particolare,
  [math]c[/math]
  sarà un punto di minimo se la derivata
  [math]n[/math]
  -esima calcolata in
  [math]c[/math]
  è positiva, di massimo se questa è negativa;
• se
  [math]n[/math]
  è dispari, allora il punto
  [math]c[/math]
  è un punto di flesso a tangente orizzontale; in particolare,
  [math]c[/math]
  sarà un punto di flesso ascendente se la derivata
  [math]n[/math]
  -esima calcolata in
  [math]c[/math]
  è positiva, e discendente se questa è negativa;

Potrebbero interessarti

• Asintoti e studio di funzione
• Esempi di studio di funzione
• Videolezione: Studio della funzione ( f(x) = frac{2x}{x^2-1} )
• Studi di funzione completamente risolti