Cambiamenti di riferimento nel piano

di _stan

(320 punti)

6' di lettura

Nel piano cartesiano, i punti hanno una precisa posizione, espressa dalle loro coordinate.

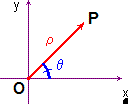
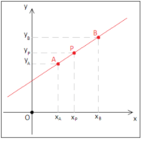
Tuttavia, uno stesso punto può avere coordinate diverse in base al riferimento che stiamo considerando.

Quindi, l'intera equazione di una curva esiste ed è tale in base al tipo di riferimento che consideriamo.

Vediamo ora alcuni tipi di cambio di riferimento.

Traslazione degli assi

Consideriamo i riferimenti cartesiani xOy e XO'Y, paralleli ed equiversi, e ipotizziamo che O' abbia, nel riferimento xOy, coordinate (( x_0 ; y_0 )).

Consideriamo il punto P che nei due riferimenti ha coordinate, rispettivamente, ( x ; y ) e ( X ; Y ); allora, le sue coordinate nei due riferimenti sono legate dalle seguenti formule di traslazione:

[ \begin{cases} X = x - x_0 \ Y = y - y_0 end{cases} ,,,, , ,,,, \begin{cases} x = X + x_0 \ y = Y + y_0 end{cases} ]

Grazie a queste formule, possiamo passare dal vecchio sistema di riferimento (xOy) all'altro (XO'Y), traslato rispetto al primo, e viceversa, se conosciamo le coordinate della nuova origine rispetto al vecchio riferimento.

Rotazione degli assi

Consideriamo due riferimenti cartesiani xOy e XOY, di cui quest'ultimo risulta essere ruotato di un angolo (alpha) rispetto al primo.

Consideriamo un punto P che ha coordinate ( x ; y ) rispetto al riferimento di partenza, e coordinate ( X ; Y ) rispetto al riferimento ruotato.

Se conosciamo le coordinate del punto P rispetto al sistema xOy, possiamo determinare le sue coordinate rispetto al sistema XOY mediante le seguenti formule:

[ color{red}{\boxed{color{black}{ \begin{cases} X = xcos alpha + y \sin alpha \ Y = -x\sinalpha + y cosalpha end{cases} }}} ]

Da questa relazione, possiamo ottenere le formule inverse, che ci permettono di passare dal riferimento ruotato a quello di partenza.

Notiamo che questo passaggio inverso equivale ad una rotazione dello stesso angolo in senso contrario; le formule inverse, quindi, si possono ottenere semplicemente scambiando x con X, y con Y e (alpha) con (-alpha).

Abbiamo quindi le seguenti formule:

[ \begin{cases} x = Xcos (-alpha) + Y \sin (-alpha) \ y = -X\sin(-alpha) + Y cos(-alpha) end{cases} ]

Tenendo conto delle proprietà delle funzioni goniometriche, otteniamo:

[ color{red}{\boxed{color{black}{ \begin{cases} x = Xcos alpha - Y \sin alpha \ y = X\sinalpha + Y cosalpha end{cases} }}} ]

Rotazioni particolari

Applichiamo la formula della rotazione diretta nel caso di alcuni angoli particolari, di cui siano note le funzioni goniometriche.

Vediamo i casi in cui gli angoli sono multipli di 45°:

( alpha = 45° ,,,,, ( alpha = pi/4 ))

In questo caso, sappiamo che per l'angolo di 45° le funzioni seno e coseno assumono il valore di (\sqrt{2}/2); possiamo quindi scrivere le formule in questo modo:

[ \begin{cases} X=frac{\sqrt{2}}{2}x + frac{\sqrt{2}}{2}y \ Y = -frac{\sqrt{2}}{2}x+frac{\sqrt{2}}{2}y end{cases} ]

Queste formule possono anche essere scritte ricordando il prodotto matrice-vettore:

[ (X;Y) = \begin{pmatrix} frac{\sqrt{2}}{2} &frac{\sqrt{2}}{2} \ -frac{\sqrt{2}}{2} &frac{\sqrt{2}}{2} end{pmatrix} cdot (x;y) = frac{\sqrt{2}}{2} cdot \begin{pmatrix} 1 &1 \ -1 &1 end{pmatrix} cdot (x;y) ]

( alpha = 90° ,,,,,,, ( alpha = pi/2 ))

Poiché il seno vale 1 se l'angolo è di 90° e il coseno è uguale a zero, sostituendo i valori nelle formule otteniamo:

[ \begin{cases} X=y \ Y=-x end{cases} ]

Esprimendo le formule con il prodotto matrice-vettore:

[ (X;Y) = \begin{pmatrix} 0 &1 \ -1 &0 end{pmatrix} cdot (x;y) ]

(alpha = 180° ,,,,,,, ( alpha = pi ))

Per gli angoli di 180° il seno vale 0 e il coseno è uguale -1, quindi sostituendo i valori nelle formule otteniamo:

[ \begin{cases} X = -x \ Y = -y end{cases} ]

Con il prodotto matrice-vettore otteniamo la seguente scrittura:

[ (X;Y) = \begin{pmatrix} -1 &0 \ 0 &-1 end{pmatrix} cdot (x;y) ]

(alpha = 270°,,,,,,, (alpha = 3pi/2 ))

Per gli angoli di 270° il seno vale -1 e il coseno è uguale 0, quindi sostituendo i valori nelle formule otteniamo:

[\begin{cases} X=-y \ Y=x end{cases}]

Scriviamo le formule con il prodotto matrice-vettore:

[ (X;Y) = \begin{pmatrix} 0 &-1 \ 1 &0 end{pmatrix}cdot (x;y) ]

Nel caso degli angoli multipli di 30° abbiamo i seguenti casi:

(alpha = 30°,,,,, ( alpha = pi/6 ))

In questo caso, il coseno dell'angolo vale (\sqrt{3}/2), mentre il seno vale (1/2), quindi abbiamo:

[ \begin{cases} X=frac{\sqrt{3}}{2}x + frac{1}{2}y \ Y=-frac{1}{2}x+frac{\sqrt{3}}{2}y end{cases} ]

Possiamo scrivere le formule anche con la seguente notazione:

[ (X;Y) = \begin{pmatrix} frac{\sqrt{3}}{2} &frac{1}{2} \ -frac{1}{2} &frac{\sqrt{3}}{2} end{pmatrix} cdot (x;y) = frac{1}{2} \begin{pmatrix} \sqrt{3} &1 \ -1 &\sqrt{3} end{pmatrix} cdot (x;y) ]

(alpha = 60°,,,,, ( alpha= pi/3 ))

In questo caso, il seno dell'angolo vale (\sqrt{3}/2), mentre il coseno vale (1/2), quindi abbiamo:

[ \begin{cases} X = frac{1}{2}x + frac{\sqrt{3}}{2}y \ Y=-frac{\sqrt{3}}{2}+frac{1}{2}y end{cases} ]

Anche in questo caso, possiamo esprimere le formule con il prodotto matrice-vettore:

[ (X;Y) = \begin{pmatrix} frac{1}{2} &frac{\sqrt{3}}{2} \ -frac{\sqrt{3}}{2} &frac{1}{2} end{pmatrix} cdot (x;y) = frac{1}{2}cdot \begin{pmatrix} 1 &\sqrt{3} \ -\sqrt{3} &1 end{pmatrix} cdot (x;y) ]