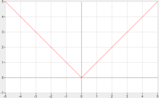
Disequazioni della forma
[math] |f(x) \lt k | [/math]
con [math] k \gt 0 [/math]
Consideriamo il caso in cui l'argomento della
valore assoluto sia
[math]x[/math]
:
[math] |x| \lt k [/math]
sapendo che
[math]k[/math]
è un numero positivo, possiamo affermare che
[math]x[/math]
può assumere tutti i valori che sono compresi tra
[math]0[/math]
e
[math]k[/math]
; ma poiché due numeri opposti hanno lo stesso valore assoluto, anche i valori compresi tra
[math]-k[/math]
e
[math]0[/math]
soddisfano l'equazione.
Possiamo quindi affermare che, essendo
[math]k[/math]
un generico numero positivo, le soluzioni sono date dai valori di
[math]x[/math]
compresi tra
[math]-k[/math]
e
[math]k[/math]
:
[math] |x| \lt k \leftrightarrow -k \lt x \lt k \mbox{ con } k \gt 0 [/math]
La stessa regola vale per
[math] |x| \le k [/math]
:
[math] |x| \le k \leftrightarrow -k \le x \le k \mbox{ con } k \gt 0 [/math]
Possiamo generalizzare la regola precedente, considerando al posto di
[math]x[/math]
una generica espressione contenente
[math]x[/math]
:
[math] |f(x)| \lt k \leftrightarrow -k \lt f(x) \lt k \mbox{ con } k \gt 0 [/math]
[math] |f(x)| \le k \leftrightarrow -k \le f(x) \le k \mbox{ con } k \gt 0 [/math]
In particolare, l'espressione
[math] -k \lt f(x) \lt k [/math]
si traduce nel seguente
sistema:
[math] \begin{cases} f(x) \lt k \\ f(x) \gt -k \end{cases} [/math]
Esempio
Consideriamo la seguente disequazione con valore assoluto:
[math] |2x -3| \lt 5 [/math]
applicando la regola vista in precedenza, abbiamo che:
[math] -5 \lt 2x -3 \lt 5 [/math]
quindi, le soluzioni della disequazione sono date dal seguente sistema:
[math] \begin{cases} 2x - 3 \lt 5 \\ 2x - 3 \gt -5 \end{cases} [/math]
risolviamo il sistema:
[math] \begin{cases} 2x \lt 5 + 3 \\ 2x \gt -5 + 3 \end{cases} \rightarrow \begin{cases} 2x \lt 8 \\ 2x \gt -2 \end{cases} \rightarrow \begin{cases} x \lt 4 \\ x \gt -1 \end{cases} [/math]
Concludiamo che le soluzioni della disequazione sono date dall'intervallo:
[math] S: -1 \lt x \lt 4 [/math]
Disequazioni della forma
[math] |f(x)| \gt k [/math]
con [math] k \gt 0 [/math]
Consideriamo il caso in cui l'argomento del valore assoluto sia semplicemente
[math]x[/math]
:
[math] |x| \gt k [/math]
possiamo notare che i valori di
[math]x[/math]
maggiori a
[math]k[/math]
verificano sicuramente la disequazione; ma poiché numeri opposti hanno lo stesso valore assoluto, sicuramente anche i valori di
[math]x[/math]
minori di
[math]-k[/math]
soddisferanno la disequazione.
In generale, quindi, essendo
[math]k[/math]
un generico numero positivo, le soluzioni della disequazione sono dati dai valori di
[math]x[/math]
maggiori di
[math]k[/math]
e minori di
[math]-k[/math]
:
[math] |x| \gt k \leftrightarrow x \lt -k \vee x \gt k \mbox{ con } k \gt 0 [/math]
[math] |x| \ge k \leftrightarrow x \le -k \vee x \ge k \mbox{ con } k \gt 0 [/math]
Possiamo estendere questa affermazione al caso in cui, al posto di
[math]x[/math]
, vi sia un'espressione contenente
[math]x[/math]
:
[math] |f(x)| \gt k \leftrightarrow f(x) \lt -k \vee f(x) \gt k \mbox{ con } k \gt 0 [/math]
[math] |f(x)| \ge k \leftrightarrow f(x) \le -k \vee f(x) \ge k \mbox{ con } k \gt 0 [/math]
Notiamo che dobbiamo risolvere due disequazioni per trovare le soluzioni della disequazione di partenza ma, in questo caso, a differenza di prima, non dobbiamo metterle a sistema, ma dobbiamo unire le loro soluzioni.
Esempio
Risolviamo la seguente disequazione con valore assoluto:
[math] |1+2x| \gt 5 [/math]
applicando la regola vista in precedenza, abbiamo che:
[math] 1+2x \lt -5 \vee 1+2x \gt 5 [/math]
Risolviamo le due disequazioni una alla volta; cominciamo dalla prima:
[math] 1+2x \lt -5 [/math]
[math] 2x \lt -5 - 1 [/math]
[math] 2x \lt -6 \rightarrow x \lt -3 [/math]
passiamo ora alla seconda:
[math] 1+2x \gt 5 [/math]
[math] 2x \gt 5 - 1 [/math]
[math] 2x \gt 4 \rightarrow x \gt 2 [/math]
Le soluzioni della disequazione di partenza sono date dall'unione delle soluzioni delle due disequazioni precedenti:
[math] S: (\infty; -3) \cup (2; +\infty) [/math]
Disequazioni con valori assoluti
Nel caso in cui non fosse possibile ricondurre una disequazione alle forme viste precedentemente, la disequazione va risolta studiando il degno dell'argomento; o nel caso in cui compiano, all'interno della disequazione, due o più valori assoluti, dobbiamo risolvere la disequazione studiando il segno degli argomenti, e risolvere i sistemi relativi ad ogni intervallo.
Vediamo alcuni esempi.
Cominciamo con una disequazione in cui compare un solo valore assoluto:
[math] |x-3| \gt 5 -3x [/math]
Dalla definizione di valore assoluto, abbiamo i seguenti due sistemi:
[math] \begin{cases} x-3 \ge 0 \\ x-3 \gt 5-3x \end{cases} \vee \begin{cases} x-3 \lt 0 \\ -(x-3) \gt 5 - 3x \end{cases} [/math]
Risolviamo il primo:
[math] \begin{cases} x \ge 3 \\ x+3x \gt 5+3 \end{cases} \rightarrow \begin{cases} x \ge 3 \\ 4x \gt 8 \end{cases} \rightarrow \begin{cases} x \ge 3 \\ x \gt 2 \end{cases} [/math]
la soluzione del sistema è l'intervallo
[math][3; +\infty)[/math]
;
Risolviamo ora il secondo:
[math] \begin{cases} x \lt 3 \\ -x+3 \gt 5-3x \end{cases}\rightarrow \begin{cases} x \lt 3 \\ -x+3x \gt 5-3 \end{cases} \rightarrow [/math]
[math] \rightarrow \begin{cases} x \lt 3 \\ 2x \gt 2 \end{cases} \rightarrow \begin{cases} x \lt 3 \\ x \gt 1 \end{cases} [/math]
La soluzione del sistema è il seguente intervallo:
[math](1; 3)[/math]
.
Le soluzioni della disequazione sono date dall'unione delle soluzioni dei due sistemi:
[math](1; 3) \cup [3;+\infty)[/math]
;
quindi, la soluzione del sistema è l'intervallo
[math](1; +\infty)[/math]
.
Vediamo ora un esempio in cui abbiamo due valori assoluti; risolviamo la seguente disequazione:
[math] |2x+4|+|x+1|-3x+1 \gt 0[/math]
Cominciamo studiando il segno degli argomenti e riportando lo studio in un grafico, in cui individuiamo i tre intervalli:

[math] 2x - 4 \gt 0 \rightarrow x \gt 2 [/math]
[math] x+1 \gt 0 \rightarrow x \gt -1 [/math]
Impostiamo il primo sistema: nel primo intervallo entrambi gli argomenti sono negativi:
[math] S_1: \begin{cases}x \lt -1 \\ -(2x-4)-(x+1)-3x+1 \gt 0 \end{cases} [/math]
[math] \begin{cases} x \lt -1 \\ -6x \gt 4 \end{cases} \rightarrow \begin{cases} x \lt -1 \\ x \lt \frac{2}{3} \end{cases} [/math]
La soluzione di questo primo sistema è l'intervallo
[math](-\infty; -1)[/math]
;
[math] S_1: (-\infty; -1)[/math]
risolviamo il secondo sistema; nel secondo intervallo il primo argomento è positivo, mentre il secondo è negativo:
[math] S_2: \begin{cases} -1 \le x \lt 2 \\ -(2x-4) + x + 1 - 3x + 1 \gt 0 \end{cases} [/math]
[math] \begin{cases} -1 \le x \lt 2 \\ -2x+4+x+1-3x+1 \gt 0 \end{cases} [/math]
[math] \begin{cases} -1 \le x \lt 2 \\ -4x \gt -6 \end{cases} \rightarrow \begin{cases} -1 \le x \lt 2 \\ x \lt \frac{3}{2} \end{cases} [/math]
Le soluzioni del secondo sistema sono:
[math] S_2: \Big[-1; \frac{3}{2} \Big) [/math]
Passiamo al terzo sistema; nel terzo intervallo entrambi gli argomenti sono positivi:
[math] S_3: \begin{cases} x \ge 2 \\ 2x-4+x+1-3x+1 \gt 0 \end{cases} \begin{cases} x \ge 2 \\ 0 \cdot x \gt 2 \end{cases} [/math]
Il sistema è impossibile, quindi abbiamo
[math] S_3: \varnothing [/math]
Sapendo che le soluzioni della disequazione iniziale sono date dall'unione di tutti gli intervalli che sono soluzione dei sistemi precedenti, abbiamo che:
[math] S = S_1 \cup S_2 \cup S_3 = (-\infty; -1) \cup \Big[-1; \frac{3}{2} \Big) \cup \varphi = \Big(-\infty; \frac{3}{2} \Big) [/math]
Potrebbero interessarti