Uno dei modi più semplici per scrivere i numeri è fare delle tacche sulla carta, o su un bastone, o per terra, a seconda di cosa si ha a disposizione. In effetti molte volte torna comodo, tranne se si devono scrivere numeri grandi. E quante tacche ci vorranno se si volesse scrivere una intera enciclopedia. Paradossalmente basta una sola tacca. Come?
Il modo più semplice di registrare l'informazione usando le tacche è quello di far corrispondere il numero 1 a una tacca, il 2 a due tacche e così via.
Al più si possono raggruppare le tacche.Un antichissimo ritrovamento risalente al 20.000 a.C., costituito da un osso di babbuino (vedi figura) e conservato nel Museo delle Scienze Narturali di Bruxelles, presenta diverse tacche raggruppate in un modo che a tutt'oggi ci è poco chiaro.
In realtà le potenzialità di rappresentare le informazioni con una tacca sono enormi.
Per esempio, è possibile memorizzare l'intera Wikipedia con una sola tacca.
Come prima cosa occorre trasformare tutta l'informazione contenuta nell'enciclopedia in un solo numero, cosa peraltro molto semplice, visto che Wikipedia si presenta già in forma digitale e quindi è già memorizzata sotto forma di numero binario. 
Un numero molto lungo certamente ma sempre un numero limitato.
Immaginiamo che scritto nel codice binario sia:
Poniamo davanti
A questo punto prendiamo un bastone lungo esattamente un metro e segniamo una tacca esattamente in un punto in modo tale che il bastone resti diviso in due segmenti a e b per i quali
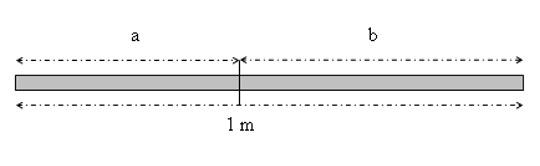
Questa tacca conserva tutta l'informazione contenuta in Wikipedia. Infatti, in qualsiasi momento sarà sufficiente misurare con estrema precisione le lunghezze di a e b e dividerle per riottenere il numero decimale che rigenera tutta Wikipedia.
Da Martin Gardner, Ah! Ci sono! Paradossi stimolanti e divertenti.
