Cos'è l'analisi funzionale
La rappresentazione grafica di una funzione fa ormai parte della cultura comune: il grafico della temperatura in un certo posto al passare del tempo, il grafico dei profitti e delle perdite di una società, il grafico della temperatura di un malato. Si dice che una certa grandezza y è funzione di un'altra grandezza x, se per ogni valore di x la funzione determina in modo univoco un valore di y. (fig. 1) Lo studio delle funzioni è stato sviluppato nel calcolo infinitesimale classico da Newton , Leibnitz , Cauchy , Weierstrass . L'Analisi Funzionale nasce alla fine del XIX secolo e si sviluppa nel XX; il nome è dovuto al matematico francese Hadamard . Tra i più celebri matematici italiani che hanno contribuito alla sua nascita è da ricordare Vito Volterra . Questa nuova e più astratta analisi non studia le singole funzioni o un numero finito di esse bensì una famiglia infinita di funzioni. Il suo problema principale è quello di organizzare questa famiglia in maniera da poterne studiare le proprietà. Si parla perciò di spazio funzionale , attribuendo alla parola spazio un significato più ampio di quello comunemente inteso. Il primo passo che bisogna compiere per organizzare lo spazio delle funzioni è quello di fissare un metodo per misurare la distanza tra una funzione e un'altra, o in modo equivalente quello di stabilire quanto una funzione si differenzia da un'altra. Osserviamo, intanto, che il modo di misurare le distanze non è univoco. Prendiamo un esempio banale. Che distanza c'è tra Lecce e Torino? Se ne può misurare la distanza in linea d'aria ma se andiamo in automobile questa informazione non ci interessa, ci interessa sapere quanta strada bisogna percorrere per arrivare a Roma. Se invece andiamo in treno non ci interessa quanta strada il treno deve percorrere ma quanto tempo ci vuole per arrivare. Se andiamo in aereo ci interessa essenzialmente il costo del biglietto. Assegnare una distanza in senso lato significa attribuire ai due enti, Lecce e Torino nell'esempio, un numero. Questo numero ci permette di fare confronti tra le varie coppie di enti, per esempio ci può servire per confrontare Lecce-Torino con Lecce-Milano o con Palermo-Venezia. In termini matematici parliamo di un spazio metrico. In che modo possiamo misurare la distanza tra una funzione e un'altra? Un modo semplice può essere quello di considerare il massimo scarto tra le due funzioni: si considerano tutte le differenze f(x)-g(x) e si individua quella che in valore assoluto è la maggiore (fig. 2) Vediamo un esempio pratico. f(x) rappresenta i ricavi di un'azienda e g(x) le sue spese, la distanza in questo caso è data dal guadagno massimo registrato in un giorno. Un altro esempio. f(x) rappresenta la temperatura di Lecce e g(x) quella di Torino; la distanza, in questo caso, è data dalla differenza massima di temperatura registrata nello stesso giorno a Lecce e a Torino. Se invece si è più interessati a una distanza media, si deve considerare l'area racchiusa tra i due grafici (fig. 3). In questo caso sapremo per esempio la differenzia media di temperatura tra Lecce e Torino. E' evidente però che il modo di misurare la distanza tra due enti, pur essendo arbitraria, deve sottostare a delle limitazioni, alcune delle quali molto evidenti. Proprietà triangolare : andare direttamente da Roma a Milano deve necessariamente essere più conveniente che passare per un'altra città; al più può essere indifferente se quest'ultima città si trova sul nostro percorso. Usando un pizzico di simbolismo d(A,B) Una seconda proprietà, o assioma, è fin troppo ovvia per il modo usuale di ragionare. Tuttavia i matematici, abituati a snidare mostruosità logiche proprio nelle cose apparentemente ovvie, ci tengono a esplicitarla. Un elemento ha distanza nulla da se stesso . La terza proprietà sembra ovvia a prima vista ma riflettendoci un po' su non lo è. Si richiede infatti che la distanza da A a B sia la stessa di quella da B a A . Nel caso in cui valga quest'ultima proprietà si parla di distanze simmetriche , nel caso opposto si parla di distanze asimmetriche . Di gran lunga più complesso è il problema di estendere il concetto di dimensione tipico dello spazio geometrico allo spazio funzionale. Vi sono diversi modi per individuare le dimensioni di un ente geometrico. Per esempio, se siamo in autostrada possiamo andare solo avanti o indietro; questo fatto ci dice che siamo in uno 'spazio' a una dimensione. Se siamo in campagna possiamo andare avanti e indietro, a destra e a sinistra: questa doppia possibilità di scelta ci dice che siamo in uno 'spazio' a due dimensioni. Se siamo sott'acqua, o siamo in aereo, possiamo andare avanti-indietro, destra-sinistra, su - giù: tre possibilità di muoverci corrispondono a tre dimensioni. Un altro modo è il seguente. Un segmento di un metro scomposto in centimetri si divide in 100 parti. Un quadrato di lato un metro scomposto in quadrati di lato un centimetro si divide in 1002 parti. Un cubo di lato un metro scomposto in cubi di lato un centimetro si scompone in 1003 parti. L'esponente del numero 100 ci dice qual è il numero di dimensioni dell'oggetto considerato. Gli spazi funzionali più interessanti dal punto di vista matematico e applicativo hanno purtroppo dimensione infinita . Si parla in questi casi di spazi di Hilbert . Uno spazio a una dimensione ha bisogno di una coordinata per individuare i suoi punti. Uno spazio a due dimensione ne ha bisogno di due, e così via. Uno spazio a infinite dimensioni necessita di una quantità infinita di coordinate. In uno spazio così mostruoso l'intuizione matematica non può fare a meno di un severo controllo logico, il quale a sua volta necessità un simbolismo astratto piuttosto complesso. Una delle applicazioni più importanti di questa branca di studi è il calcolo delle variazioni . Si tratta dell'estensione naturale della ricerca di massimi e minimi per una funzione. Invece di cercare i punti in cui la funzione assume valori massimi o minimi; si cercano, tra le tante possibili, quelle funzioni che rendono minima o massima una certa condizione. Uno dei problemi classici del calcolo delle variazioni è quello delle superfici minime: assegnata una curva dello spazio, determinare la superficie di area minima avente come bordo la curva assegnata. Un altro problema classico è quello delle geodetiche , ossia la determinazione dei percorsi più brevi su una superficie curva. Altre applicazioni importanti del calcolo delle variazioni riguardano la minimizzazione di costi (teoria dell'ottimizzazione ), la minimizzazione di certi funzionali dell'energia di sistemi fisici soggetti a vincoli naturali, per esempio i cristalli liquidi, i problemi di transizione di fase nei materiali composti, problemi di omogeneizzazione e di rilassamento dei materiali. Antonio Bernardo N.Bourbaki, Elementi di storia della matematica, Feltrinelli, Milano, 1963 E. De Giorgi, Sviluppi dell'Analisi Funzionale del Novecento , in AA.VV. Morte di un matematico napoletano , Ubulibri, Milano, 1992. C.F.Manara e G.Giorello, La m atematica nel XX secolo, in Storia delle Scienze , a cura di E.Agazzi, Città Nuova Editrice, Roma, 1984. F.Severi e F.Conforto, Caratteri e indirizzi della matematica moderna, in Enciclopedia delle matematiche elementari , a cura di L. Berzolari, Hoepli, Milano, 1962. In rete: http://gruppiindam.cs.unibo.it/gnafa/ Gruppo nazionale per l'analisi funzionale e le sue applicazioni. http://calvino.polito.it/ricerca/gruppi/gruppo8.html Gruppo di ricerca in analisi funzionale del Politecnico di Torino http://www.unict.it/mathesis/bollet7/marino.htm Un articolo del prof. M.Marino su Teoria della misura: da Cavalieri ai nostri tempi. | |
fig.1 grafico di una funzione | |
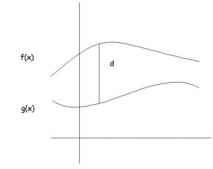 | |
fig.2 primo esempio di distanza | |
 | |
| fig. 3 distanza media | |
 | |
| fig. 4 Vito Volterra |

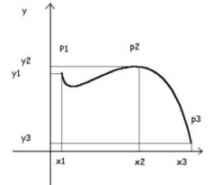 Un semplice esempio. A si trovi al livello del mare e B a 500 m di altezza. Dovendo andare in bicicletta è evidente che il percorso BA è più piacevole e più 'breve' del percorso AB.
Un semplice esempio. A si trovi al livello del mare e B a 500 m di altezza. Dovendo andare in bicicletta è evidente che il percorso BA è più piacevole e più 'breve' del percorso AB.