L'incredibile motore differenziale di Babbage

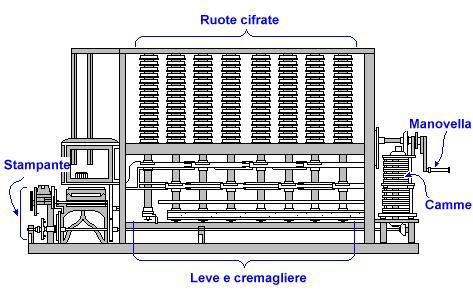
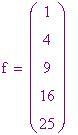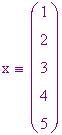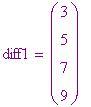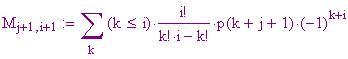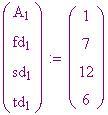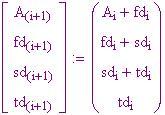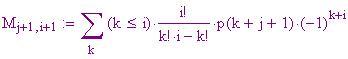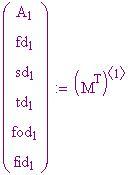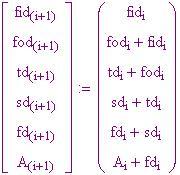Il motore differenziale N.2 di Charles Babbage pesava tre tonnellate, non aveva parti elettroniche e calcolava i valori dei polinomi del settimo grado con la precisione di 31 cifre decimali. Questo calcolatore meccanico aveva più di 4.000 componenti ed era azionato a mano. Se tutto ciò può stupire, è incredibile sapere che è stato progettato nel 1 847!

La motivazione primaria per la costruzione di un simile strumento era l'incredibile numero di errori presenti nelle tabelle matematiche del tempo, che descrivevano valori di vari polinomi per sequenze di dati di ingresso .

Il problema: valutare polinomi

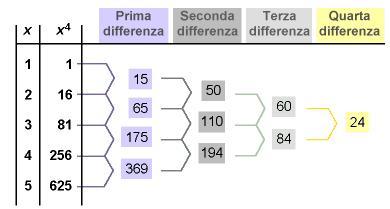
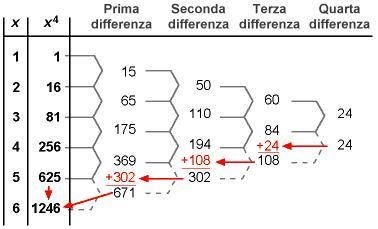
Il calcolo dei valori dei polinomi viene fatto meccanicamente dal motore differenziale che si basa sul metodo delle differenze finite. Per capire come funziona matematicamente questo metodo prendiamo come esempio di polinomio e troviamo le sequenze di differenza per i primi cinque valori, . La prima serie di differenze, , viene elencata sotto

Prima serie di differenze:

La seconda serie di differenze viene acquisita dalla prima serie in maniera simile. Ciò prosegue fino alla -sima differenza, dove rappresenta l'ordine del polinomio(in questo caso 2). Il risultato dalla differenza ennesima sarà una costante, come si può vedere in .

La costante rimasta alla fine della catena di differenze risulta . Attenti a cosa accade più in generale. Le differenze vengono determinate come:

… e così via fino all'ennesimo valore di e la ennesima differenza.

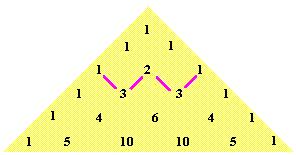
Lo Schema delle Differenze

Succede che se è un polinomio di grado , allora la colonna in una tabella di differenze sarà costituita da una costante diversa da zero. Come si è appena visto sopra nel polinomio di secondo grado , la terza fila, costituita dalla seconda serie di differenze, era costantemente 2. Si può riconoscere sopra la sequenza di numeri davanti ai come coefficienti di binomi alternanti oppure come le immissioni nel Triangolo di Pascal:

La esima entrata nell' esima colonna è . Usando questa espressione, possiamo calcolare l'intera matrice delle differenze per un dato polinomio. Di nuovo, x 2 sarà usato come esempio. Nota cosa succede: i termini del polinomio di varia potenza si cancellano, eccetto che per le costanti, che non sono uniformi nei termini , e così via, come nell'esempio seguente:

e così via, lasciando solo una costante nell'ultima differenza.

Dato un qualunque polinomio, sapreste determinare quale sarà la fila di costanti diverse da zero? Suggerimento: provate , poi , poi , e .

Provate anche .

Usare le Differenze per Ricostruire i Valori

Data questa informazione, il metodo può essere capovolto per trovare tutti gli altri valori del polinomio nei punti di numero intero; operatore unico è l'addizione. Questa procedura viene illustrata nella tabella che segue per . Questo procedimento deve iniziare con i primi valori consecutivi , cioè . Da lì, verranno trovate le prime quattro differenze. La quarta differenza (o quinta colonna) sarà una colonna di costanti. Usando questa costante possiamo ricostruire termini aggiuntivi usando l'addizione, come si dimostra nella tabella sottostante.

Controlla per :

La quarta differenza viene usata per aggiungere un'ulteriore immissione alla terza differenza. Usiamo questo nuovo numero per trovare la successiva immissione nella fila delle seconde differenze. Si continua così fino a che non si trova una nuova immissione nella prima fila dei valori di costante, cioè, un valore per .

Come riesce a farlo il Motore

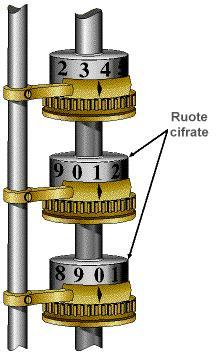
Meccanicamente, questo calcolo inizia girando la manovella a lato del motore differenziale nell'illustrazione all'inizio di questo documento. Ciò fa entrare in azione 14 paia di camme, che controllano la sincronizzazione dell'intero meccanismo.

Ci sono otto colonne di ingranaggi, ognuna delle quali contiene 31 ruote numerate, usate per fissare i valori di inizio del calcolo. Il motore deve essere preimpostato con numeri di inizio calcolati a mano, come si diceva sopra. Le ruote sono sbloccate e ruotate fino al valore iniziale corretto.

Le camme sono collegate alle otto colonne da cremagliere e bracci. Ogni giro del manubrio alza, abbassa e fa girare l'asse della colonna delle ruote numerate che compiono l'addizione delle differenze.

Il risultato finale del calcolo è contenuto nell'ultima colonna di ruote, collegata ad una macchina stampante. Questa macchina stampa un valore di trenta cifre per il polinomio ad ogni giro di manovella. Ad ogni giro il valore di immissione è aumentato automaticamente di uno ( ).

Questo metodo richiede un numero specifico di valori diversi di inizio basati sull'ordine del polinomio. Se l'equazione è di ordine , ci devono essere valori calcolati (il polinomio stesso e le differenze) per poter arrivare alle valutazioni polinomiche successive. Simuleremo ora il metodo delle differenze finite per come veniva impiegato meccanicamente per trovare valori di f . Diamo alla simulazione la serie di valori calcolati, che equivale a predisporre le ruote numerate.

Numero di elementi nella tavola dei valori.

Vettore della prima risposta ad ogni colonna di differenze. Va notato che, per un polinomio di grado 3, sono necessari quattro valori iniziali .

Qui, corrisponde alla esima immissione nella fila delle prime differenze. Nello stesso modo , corrisponde alle seconde differenze e alle terze.

Una iterazione distribuita in un vettore emula il motore differenziale molto bene. Il meccanismo non poneva in memoria i numeri, ma li stampava man mano che venivano calcolati. L'ultima serie di risposte veniva conservata in registri per utilizzarla nella successiva serie di calcoli.

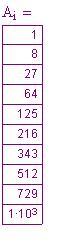
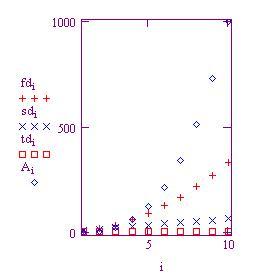
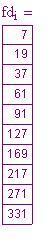
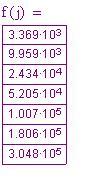
La seguente tabella e grafico fanno vedere le risposte calcolate con questo metodo. La tabella è sfalsata per far vedere le giuste relazioni delle differenze:

IL grafico mostra dieci valori per la funzione e ogni differenza. Va ricordato che ogni differenza riduce il grado di uno. Così, , la fila di valori di funzione è di terzo grado poiché . è di quarto grado, così il suo grafo è una parabola.------------- di primo grado, così è lineare . Poiché è un polinomio di grado zero - una costante - ciò spiega perché il grafo è una linea piatta.

Un Esempio

Dato un qualunque polinomio . Il motore differenziale potrebbe trovare valori per per ogni numero intero, se si avesse abbastanza pazienza e un braccio robusto. L'esempio che segue calcola per i primi cento valori interi positivi di .

Potremmo trovare i valori iniziali delle differenze calcolandole a mano, come prima, ma questa volta lasciamo che sia il nostro software a computarle.

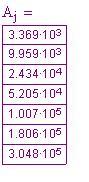
Sei valori iniziali che corrispondono ad una equazione di quinto grado.

Le colonne delle differenze quinte(rappresentata dalla sesta colonna) dovrebbero essere costante

Questi sono i primi sei valori del polinomio (prima colonna) con la tabella delle differenze.

I valori di cui abbiamo bisogno per dare il via al procedimento iterativo rappresentano la prima fila della matrice qui sopra.

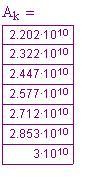
Lasciamo che l'iterazione scorra per 100 passi:

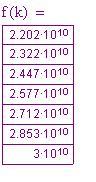
Diamo un'occhiata ad alcuni valori determinati.

Calcolo

Babbage

Calcolo

Babbage

Da notare che il calcolo fa uso di logaritmi e funzioni esponenziali per determinare i valori di nei vari valori di . La macchina di Babbage, invece, si serve solo della addizione!

Charles Babbage non vide mai la sua prodigiosa macchina pienamente operativa. Il suo Motore No.1 (una versione primitiva della No.2) era finanziata dal governo Britannico, che però abbandonò il progetto nel 1842 dopo aver speso 17,470 sterline e completando 12000 delle 25000 parti previste. Per avere un confronto, basti pensare che una delle prime locomotive a vapore costruita nel 1831 costò 784 sterline.

Avrebbe mai funzionato? Grazie al museo della scienza di Londra, un modello funzionante in scala 1:1 venne completato il 29 novembre 1991 per un costo di