2016 Esempio di seconda prova di Fisica per gli esami di stato liceo scientifico

La simulazione dell'esame di fisica per la maturità scientifica.

Problema n. 1

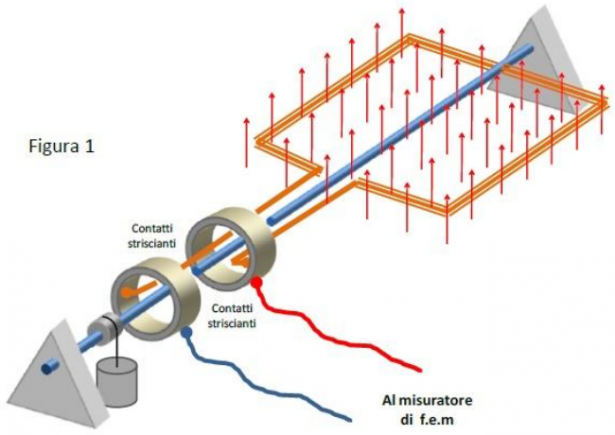
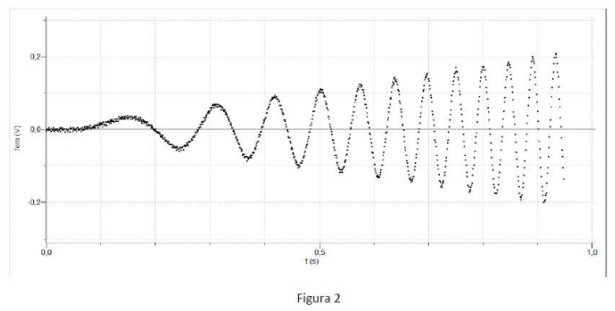
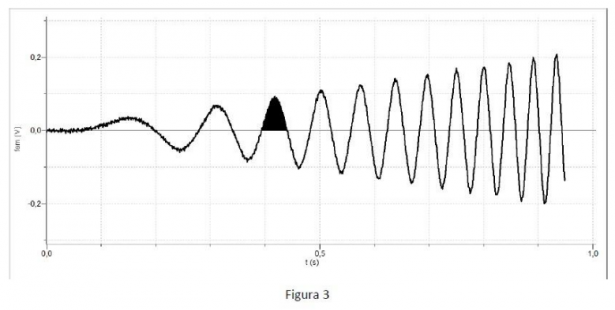
In laboratorio è stato preparato il dispositivo rappresentato in Figura 1. La bobina è costituita da 100 spire rettangolari di rame i cui lati misurano 25 cm e 30 cm. La bobina può ruotare con attrito trascurabile intorno al suo asse e durante la rotazione le estremità del filo strisciano su due anelli conduttori, mantenendo con essi un contatto elettrico. La bobina è immersa in un campo magnetico uniforme e costante. Sull’asse della bobina è montato un cilindro intorno al quale è avvolto un filo. All’estremità del filo è sospeso un pesetto. Quando il pesetto viene lasciato libero, esso cade verso il basso mettendo in rotazione la bobina. Alla partenza del pesetto il piano della spira è perpendicolare alla direzione del campo magnetico. Durante la rotazione della bobina, alle sue estremità, che restano aperte in modo che non circoli corrente, si produce una f.e.m. il cui valore viene rilevato da un sistema di acquisizione automatico che acquisisce 1000 valori al secondo. In Figura 2 sono stati riportati i dati sperimentali acquisiti dal sistema. Questo grafico rappresenta in ordinata la f.e.m. prodotta alle estremità della bobina durante la cadut a del pesetto ed in ascissa il tempo. La Figura 3 rappresenta lo stesso grafico di Figura 2. In quest’ultimo grafico i punti sperimentali sono stati uniti da segmenti per migliorarne la leggibilità.

1. Spiega il fenomeno fisico che produce la f.e.m. alle estremità della bobina e, sulla base di esso, spiega il particolare andamento del grafico sperimentale.
2. Utilizza la legge del fenomeno fisico per dedurre teoricamente la funzione matematica
   [math]y = f(t)[/math]
   che descrive la f.e.m. alle estremità della bobina in funzione del tempo e verifica che la funzione ottenuta, coerentemente con il grafico sperimentale, abbia ampiezza crescente e periodo decrescente. Considera l’intensità del campo magnetico B e l’accelerazione angolare (alpha) della bobina come parametri. Considera inoltre aperte le estremità della bobina.
3. Deduci dal grafico sperimentale le informazioni quantitative necessarie per determinare il valore dell’accelerazione angolare della bobina e l’intensità del campo magnetico i n cui ruota la bobina.
4. Spiega qual è il significato fisico dell’area, evidenziata in Figura 3, compresa tra ogni semiperiodo e l’asse dei tempi. Verifica, utilizzando la funzione
   [math]y = f(t)[/math]
   , che queste aree hanno, in modulo, tutte lo stesso valore.

Problema n. 2

Negli anni 1963 - 1964 il fisico W. Bertozzi con la sua equipe realizzò un esperimento al MIT di Boston verificando l’esistenza di una velocità limite, pari a quella della luce nel vuoto. Secondo la fisica classica è possibile accelerare un corpo dalla quiete fino a una velocità qualunque, per quanto grande essa sia, mentre per la relatività questo non è possibile. L’esperimento consiste nell’accelerare elettroni attraverso opportuni campi elettrici prodotti da una un acceleratore di Van de Graaff e da un acceleratore lineare a radiofrequenza (LINAC). Il fascio di elettroni è prodotto da un catodo caldo, sottoforma di impulsi della durata di 3 ns () e viene accelerato dall’acceleratore di Van de Graaff attraverso differenze di potenziale variabili fino a un massimo di 1,5 milioni di volt. Gli elettroni, usciti dall’acceleratore di Van de Graaff, attraversano un tubicino metallico posto in A nel quale inducono un impulso di corrente che viene inviato al l’oscilloscopio (vedi Figure 1 e 2). Il tragitto da A e B è lungo 8,40 m ed è privo di aria e di campi elettrici che possano modificare la velocità degli elettroni (l’acceleratore LINAC è spento in una prima fase dell’esperimento e in particolare non è utilizzato nelle prime tre misure di sotto riportate). Arrivati in B gli elettroni urtano un disco di alluminio nel quale provocano un impulso di corrente che viene inviato anch’esso all’oscilloscopio. Sull’oscilloscopio la distanza tra i due impulsi dà la misura del tempo impiegato dagli elettroni per andare da A a B e quindi, nota la distanza AB, è possibile calcolare la loro velocità. Ogni quadretto del reticolo dell’oscilloscopio (divisione) corrisponde a un tempo di circa ().

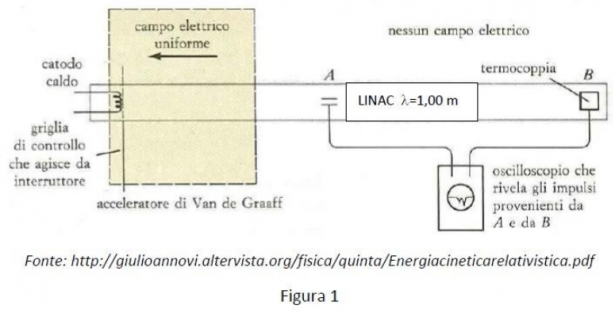
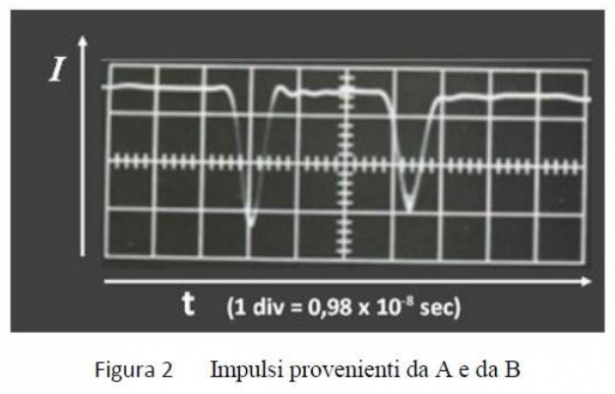
Leggendo sull’oscilloscopio la distanza tra i due impulsi, al variare della differenza di potenziale applicata dall’acceleratore agli elettroni, si ottengono i seguenti valori.

Tabella 1

Differenza Potenziale ((10^6 V))	0,5	1,0	1,5
N° divisioni tra i due impulsi	3,30	3,10	2,95

In una seconda fase dell’esperimento, per aumentare ulteriormente l’energia degli elettroni viene utilizzato anche l’acceleratore lineare (LINAC) presente nel primo metro successivo al punto A, nel quale gli elettroni vengono accelerati da ulteriori 3,0 milioni di volt. Nell’esperimento viene anche misurato il calore prodotto dagli elettroni sul disco B adoperando una termocoppia, e la carica incidente sullo stesso disco B, per mezzo di un misuratore di cariche. I risultati ottenuti per due diversi valori di differenza di potenziale complessiva sono (Tabella 2):

Tabella 2

Differenza Potenziale ((10^6 V))	1,5	4,5
Energia del fascio B (J)	10,0	29,2
Carica del fascio in B ((mu C))	6,1	6,1

Dopo questa breve esposizione, ti viene richiesto di:

1. Analizzare l’esperimento descritto e rappresentare in un piano cartesiano l’andamento di
   [math]\frac{v^2}{c^2}[/math]
   , dove
   [math]v[/math]
   è la velocità degli elettroni nel punto B e
   [math]c[/math]
   è la velocità della luce nel vuoto, in funzione del lavoro W compiuto dal campo elettrico nell’acceleratore, sia per i valori di velocità previsti dal modello classico che per i valori effettivamente misurati nell’esperimento.
2. Individuare il modello fisico più adatto a descrivere la situazione sperimentale, relativamente all’andamento di
   [math]\frac{v^2}{c^2}[/math]
   , in funzione del lavoro W compiuto dal campo elettrico nell’acceleratore.
3. Calcolare i valori di
   [math]\frac{v^2}{c^2}[/math]
   attesi in base al modello fisico individuato, confrontandoli con quelli sperimentali e discutere l’andamento atteso.
4. Verificare, utilizzando i dati di Tabella 2 nei casi di differenza di potenziale 1,5 e 4,5 milioni di volt, che l’energia cinetica posseduta dagli elettroni quando arrivano in B è circa uguale a quella fornita dall’acceleratore, giustificando così la seguente affermazione: “Il fatto che il valore della velocità misurata sia inferiore a quello previsto dalla fisica classica non è dovuto a perdite di energia nell’apparato”.

Quesiti

Quesito 1

Una lampadina a incandescenza di potenza = emette luce i n maniera isotropa. Se viene posta al centro di una stanza cubica di lato , quanta energia arriverà in 10 minuti sul soffitto della stanza?

Quesito 2

Un elettrone e un positrone (antiparticella dell’elettrone con la stessa massa dell’elettrone, ma con carica opposta) si muovono uno contro l’altro con la stessa velocità. L’energia posseduta da entrambe le particelle è di . Sapendo che la loro massa a riposo è di , qual è la velocità del positrone nel sistema di riferimento dell’elettrone?

Quesito 3

Un atomo di idrogeno si trova in uno stato eccitato dopo aver assorbito un fotone ultravioletto di lunghezza d’onda (lambda= 97,2 nm) . Questo atomo può riportarsi allo stato fondamentale seguendo diverse transizioni a ognuna delle quali corrisponde la emissione di luce di una particolare lunghezza d’onda. Quante sono le transizioni possibili che provocano emissione di fotoni con lunghezz a d’onda diversa da quella del fotone assorbito? Quali tra queste transizioni provocano emissione nel visibile? (costante di Rydberg : )

Quesito 4

Un’antenna ricevente semplificata è costituita da una spira di rame di forma quadrata. Il lato della spira misura 20 cm e le sue estremità sono collegate ad un voltmetro. Quest’ultimo è impostato in modo da fornire il valore efficace della f.e.m. ai capi della spira, ovvero dove è il valore massimo di una f.e.m. alternata.

L’antenna ricevente è posta a 100 m dall’antenna di una radio ricetrasmittente. Quest’ultima è del tipo utilizzato dai radioamatori. Queste radio trasmettono ad una frequenza di

e la legge impone loro di trasmettere con una potenza non superiore a per non disturbare la ricezione delle trasmissioni radiofoniche e televisive. Talvolta i radioamatori non rispettano questo limite e trasmettono con potenze che possono arrivare a . Si vuole stabilire se la ricetrasmittente in esame rispetta il limite di potenza imposto dalla legge. Il nostro voltmetro misura il massimo della f.e.m. quando il piano della spira è parallelo alla direzione di propagazione dell’onda e perpendicolare al campo magnetico, come mostrato in figura. Il valore efficace di questa f.e.m. è di . Qual è la potenza emessa dall’antenna della ricetrasmittente?

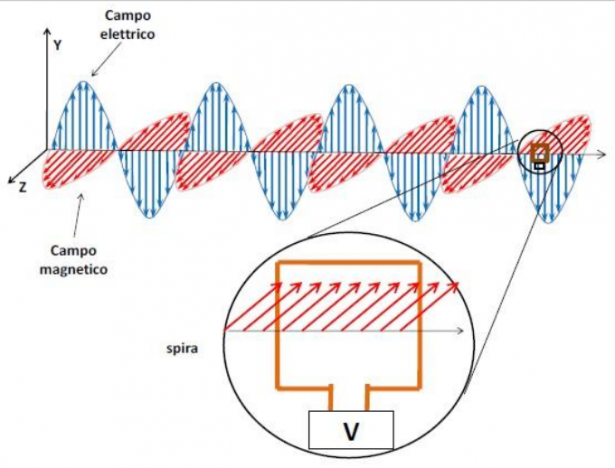
Quesito 5

Nel grafico sono rappresentati i livelli energetici di una particella di massa confinata in una buca di potenziale infinita unidimensionale (detta anche pozzo). Utilizzando il principio di de Broglie e assumendo chela funzione d’onda stazionaria si annulli sui bordi della buca, determina la massa della particella.

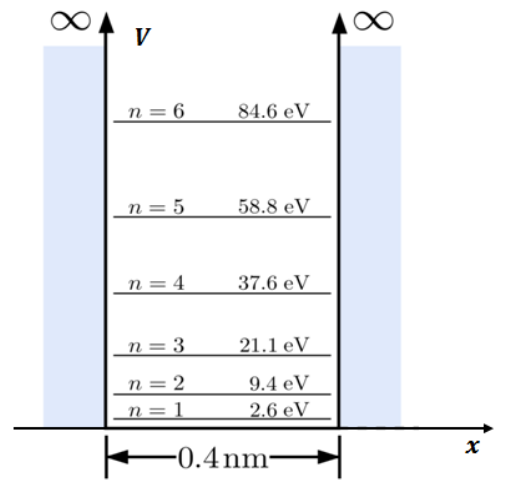
Quesito 6

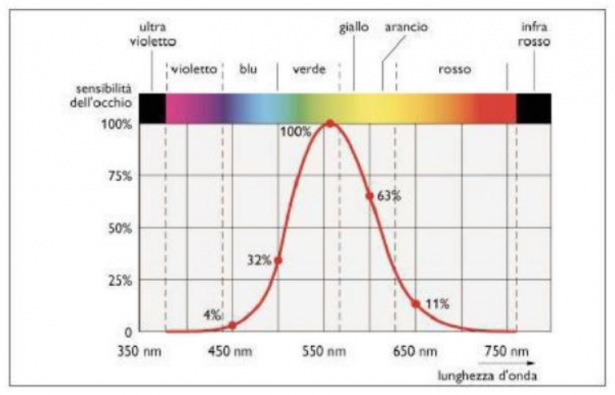
La figura riportata di seguito mostra come varia la sensibilità relativa percentuale del nostro occhio al variare della lunghezza d’onda nello spettro visibile. Il massimo della sensibilità (posto pari a 100%) si ha per =555 nm.

Fonte: http://www.progettazioneottica.it/unita-fotometriche-lumen-candele-lux/1172

NOTA: La sensibilità assoluta del nostro occhio per una particolare lunghezza d’onda è definita come il rapporto tra l’energia che viene inviata dalla retina al cervello (ad esempio sotto forma di corrente elettrica) e l’energia dell’onda elettromagnetica incidente sulla retina. La sensibilità relativa percentuale per una particolare lunghezza d’onda è definita come il rapporto tra la sensibilità assoluta a quella lunghezza d’onda e la sensibilità assoluta alla lunghezza d’onda

nm, il tutto moltiplicato per 100.

Utilizzando i dati del grafico di figura (usa solo le lunghezze d’onda per cui sono riportati i valori della sensibilità relativa percentuale in forma numerica) traccia un grafico approssimativo che indichi di quanto deve aumentare l’intensità della radiazione incidente sulla retina dell’occhio, in modo che l’energia inviata dalla retina al cervello alle varie lunghezze d’onda sia la stessa (si ponga uguale a 1 l’intensità pari alla massima sensibilità relativa). Determina, inoltre, quanti fotoni a

devono giungere sulla retina affinché essa invii al cervello la stessa energia che invia quando su di essa giungono 1000 fotoni di lunghezza d’onda .

Esempio di seconda prova di Fisica per gli esampi di stato del liceo scientifico, a.s. 2016-2017, con le relative soluzioni.