Scritta l'equazione della
circonferenza tangente in
[math]O[/math]
alla retta
[math]t: 2x - y = 0[/math]
e passante per
[math] A ( 2 ; 0 ) [/math]
, determinare l'equazione della
parabola con asse di simmetria parallelo all'asse
[math]y[/math]
, con vertice nel centro
[math]C[/math]
della
circonferenza e passante per l'origine degli assi
[math]O[/math]
.
Svolgimento
Determiniamo le coordinate del centro della circonferenza, considerando la rette passante per lo stesso e perpendicolare alla tangente
[math]t[/math]
; chiamiamo questa retta con
[math]s[/math]
:
[math]s : ax + by + c = 0 [/math]
Sapendo che la retta
[math]t[/math]
è tangente in
[math]O[/math]
alla circonferenza, anche la retta s passerà per
[math]O[/math]
, quindi la sua equazione diventa:
[math]s : ax + by = 0 [/math]
Sappiamo che il coefficiente angolare della retta
[math]t[/math]
è:
[math]m_t = - a/b = - 2/(-1) = 2 [/math]
Sapendo che la retta s è perpendicolare a
[math]t[/math]
, il suo
coefficiente angolare sarà uguale e opposto:
[math] m_s = - 1/2 [/math]
In questo caso possiamo scrivere la sua equazione così:
[math]s : x + 2y = 0 [/math]
Consideriamo ora la retta formata dall'origine e dal punto
[math]A[/math]
; possiamo affermare che il centro della circonferenza passa per la retta perpendicolare ad
[math]OA[/math]
e passante per il suo punto medio.
Essendo
[math]A[/math]
di coordinate
[math](2;0)[/math]
il punto medio del segmento
[math]OA[/math]
è
[math]M(1;0)[/math]
; la retta che cerchiamo è quindi
[math]r : x = 1 [/math]
.
Impostando un sistema fra queste due rette, possiamo risalire alle coordinate del centro della circonferenza:
[math][/math]
left{ \begin{array}{rl}
x + 2y = 0 &\
x = 1 &
end{array}\right.
[math][/math]
[math][/math]
left{ \begin{array}{rl}
y = - 1/2 &\
x = 1 &
end{array}\right.
[math][/math]
Otteniamo quindi il punto
[math] C (1 ; - 1/2)[/math]
Avendo il centro ed un punto appartenente alla circonferenza, possiamo determinare il suo raggio:
[math] R = CO = \sqrt{(x - x_1)^2 + (y - y_1)^2} = \sqrt((1-0)^2 + (-1/2 - 0)^2) = [/math]
[math] \sqrt{ 1 + 1/4} = frac(\sqrt5)(2) [/math]
Ricaviamo l'equazione della circonferenza:
[math] C : (x - x_0)^2 + (y - y_0)^2 = R^2 [/math]
[math] C : (x - 1)^2 + (y - (-1/2))^2 = (frac(\sqrt5){2})^2 [/math]
[math] C : x^2 + 1 - 2x + y^2 + 1/4 + y - 5/4 = 0[/math]
[math] C : x^2 + y^2 - 2x + y = 0 [/math]
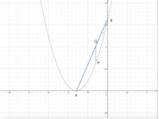
Rappresentiamo la circonferenza sul piano cartesiano:

Ora, determiniamo l'equazione della parabola; sappiamo che essa ha asse parallelo all'asse
[math]y[/math]
, quindi la sua equazione sarà del tipo
[math]y = ax^2 + bx + c[/math]
.
Le coordinate del suo vertice, coincidente con il centro della circonferenza, sono
[math](-b/(2a) ; - ∆/(4a))[/math]
.
Conoscendo le coordinate del centro della circonferenza, possiamo scrivere che:
[math] - frac(b)(2a) = 1 \to -b = 2a \to b = - 2a [/math]
Inoltre, poiché anche la parabola passa per l'origine degli assi abbiamo che:
[math] O ∈ P \to c = 0 [/math]
Possiamo poi imporre il passaggio della circonferenza per il suo vertice:
[math] V ∈ P \to C (1 ; - 1/2) ∈ P \to - 1/2 = a + b + c [/math]
mettiamo a sistema le tre scritture:
[math][/math]
left{
egin{array}{ll}
b = - 2a&\
c = 0&\
a + b + c = - 1/2 &
end{array}
ight.
[math][/math]
Risolvendo per sostituzione:
[math][/math]
left{
egin{array}{ll}
b = - 1&\
c = 0&\
a = 1/2 &
end{array}
ight.
[math][/math]
Abbiamo quindi l'equazione della parabola:
[math] y = 1/2 x^2 - x [/math]
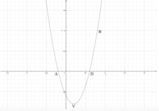
Rappresentiamola sul piano cartesiano: