_francesca.ricci
di _francesca.ricci
(70 punti)
2' di lettura
Sono date cinque semirette
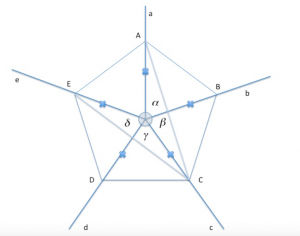
[math]a[/math]
,
[math]b[/math]
,
[math]c[/math]
,
[math]d[/math]
,
[math]e[/math]
, tutte di origine
[math]O[/math]
, formanti i quattro angoli congruenti
[math]ab[/math]
,
[math]bc[/math]
,
[math]cd[/math]
,
[math]de[/math]
. Su tali semirette prendi rispettivamente i punti
[math]A[/math]
,
[math]B[/math]
,
[math]C[/math]
,
[math]D[/math]
,
[math]E[/math]
in modo che sia
[math]OA = OB = OC = OD = OE [/math]
.

Dimostra che

[math]AC = CE [/math]
e
[math]AB = BC = CD = DE[/math]
.

Svolgimento

Consideriamo i triangoli
[math]AOE[/math]
e
[math]AOB[/math]
.
Essi hanno:
  • [math]EO = BO[/math]
    per ipotesi;
  • [math]AO[/math]
    in comune;
  • [math]hat{EOA} = hat{AOB}[/math]
    per ipotesi;
Quindi, per il primo criterio di congruenza dei triangoli, avendo due lati e l'angolo fra essi compreso congruente, i triangoli
[math]AOE[/math]
e
[math]AOB[/math]
sono congruenti.

Possiamo dedurre quindi che

[math]AE = AB[/math]
.

Seguiamo lo stesso ragionamento per i triangoli

[math]BOC[/math]
,
[math]COD[/math]
e
[math]DOE[/math]
, tutti tra loro congruenti per il primo criterio di congruenza, avendo due lati e l'angolo fra essi compreso congruente.

Abbiamo quindi dimostrato che

[math]AB = BC = CD = DE = EA[/math]
.

Ora consideriamo i triangoli

[math]AOC[/math]
e
[math]EOC[/math]
; essi hanno:
  • [math]EO = AO [/math]
    per ipotesi;
  • [math]OC[/math]
    in comune;
  • [math]hat{EOC} = hat{AOC}[/math]
    perché somme di angoli congruenti;
Quindi, per il primo criterio di congruenza dei triangoli, avendo due lati e l'angolo fra essi compreso congruente, i triangoli
[math]AOC[/math]
e
[math]EOC[/math]
sono congruenti.

In particolare risulta che

[math]AC = CE[/math]
.
Vuoi approfondire Geometria - Formule e problemi di geometria con un insegnante esperto?
Trovalo su Ripetizioni.it