[math]hat{ABC}[/math]
e un punto [math]O[/math]
esterno, si unisca [math]O[/math]
con i vertici del triangolo e si prolunghi ciascun segmento in modo che
[math]\bar(OA)~=\bar(OA'), \bar(OB)~=\bar(OB'), \bar(OC)~=\bar(OC')[/math]
.Dimostrare che il triangolo
[math]hat{ABC}[/math]
è congruente a [math]hat{A'B'C'}[/math]
.
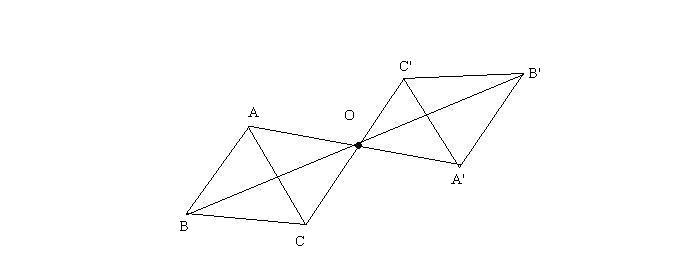Ipotesi[math]\bar(OA)~=\bar(OA')[/math]
[math]\bar(OB)~=\bar(OB')[/math]
[math]\bar(OC)~=\bar(OC')[/math]
Dimostrazione
Tesi:
[math]hat{ABC}~=hat{A'B'C'}[/math]
.I triangoli
[math]hat{ABC}[/math]
e [math]hat{A'B'C'}[/math]
sono congruenti, infatti per il primo criterio si ha[math]\bar(OA)~=\bar(OA')[/math]
per costuzione[math]\bar(OC)~=\bar(OC')[/math]
per costuzione[math]Aha OC~=A'ha OC'[/math]
perchè opposto al verticedi conseguenza
[math]\bar(AC)~=\bar(A'C')[/math]
.Analogamente
[math]hat{ABO}~=hat{A'BO}[/math]
quindi [math]\bar(AB)~=\bar(A'B')[/math]
Analogamente
[math]hat{BOC}~=hat{B'OC'}[/math]
quindi [math]\bar(BC)~=\bar(B'C')[/math]
In conclusione i triangoli
[math]hat{ABC}[/math]
e [math]hat{A'B'C'}[/math]
sono congruenti per il terzo criterio.
