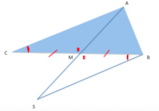
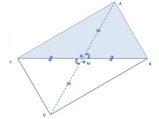
Dimostrare che un triangolo avente un lato coincidente con la base
[math]BC[/math]
di un triangolo isoscele [math]ABC[/math]
e il vertice opposto [math]D[/math]
in un punto della bisettrice dell'angolo al vertice di [math]ABC[/math]
, è isoscele. Svolgimento:
Consideiamo un triangolo isoscele[math]ar(ABC)[/math]
con vertice [math]A[/math]
e base [math]ar(BC)[/math]
. Mandiamo la bisettrice di [math]A[/math]
che interseca in [math]F[/math]
la base [math]ar(BC)[/math]
e su queta semiretta prendiamo un punto [math]D[/math]
. Ora tracciamo il triangolo [math]ar{BCD}[/math]
. Ricordiamo, ora, il teorema che dice "in un triangolo isoscele, la bisettrice dell'angolo opposto alla base è anche altezza e mediana della base". Considera i triangoli [math]ar{BDF}[/math]
e [math]ar{DCF}[/math]
aventi i lati [math]ar(BF)[/math]
e [math]ar(BC)[/math]
congruenti (per il teorema di prima la bisettrice è mediana); e uguale l'angolo retto [math]DhatFB[/math]
e [math]DhatFC[/math]
(la bisettrice è altezza, quindi [math]BhatFA[/math]
e [math]ChatFA[/math]
sono retti e [math]DhatFB[/math]
, [math]DhatFC[/math]
sono gli angoli opposti ad un vertice e quindi uguali entrambi ad angolo retto), inoltre hanno [math]ar(DF)[/math]
in comune. I due triangoli sono quindi congruenti e come tali hanno congruente anche l'angolo [math]BhatDF=DhatCF[/math]
. In conclusione il triangolo [math]ar(BCD)[/math]
quindi ha gli angoli alla base congruenti è quindi è isoscele.